AP Statistics Curriculum 2007 IntroUses
From Socr
m (→Approach) |
|||
| (24 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
| - | + | [[AP_Statistics_Curriculum_2007 | General Advance-Placement (AP) Statistics Curriculum]] - Uses and Abuses of Statistics | |
| - | == | + | ==Uses and Abuses of Statistics== |
| - | + | Statistics is the science of variation, randomness and chance. As such, statistics is different from the [http://en.wikipedia.org/wiki/Isaac_Newton Newtonian sciences], where the processes being studied obey exact deterministic mathematical laws and typically can be described as [http://en.wikipedia.org/wiki/Category:Equations systems]. Since statistics provides tools for data understanding where no other science can, one should be prepared to treat this new power of knowledge with uncertainty. In general, statistical analysis, inference and simulation will not provide deterministic answers and strict (e.g., yes/no, presence/absence) responses to questions involving stochastic processes. Rather, statistics will provide quantitative inference represented as long-time probability values, confidence or prediction intervals, odds, chances, etc., which may ultimately be subjected to varyious interpretations. | |
| - | + | ||
| - | + | This possibility of multiple interpretations may be viewed by some as detrimental or inconsistent. However, some others may consider these outcomes as beautiful, scientific and elegant responses to challenging problems that are inherently stochastic. The phrase ''Uses and Abuses of Statistics'' refers to the notion that in some cases statistical results may be used as evidence to seemingly opposite these. However, most of the time, common [http://en.wikipedia.org/wiki/Logic principles of logic] allow us to disambiguate the obtained statistical inference. [[AP_Statistics_Curriculum_2007_IntroUses#References | Some appropriate probability and statistics quotes are provided in the references section]]. | |
| - | + | ||
| - | + | ==Approach== | |
| + | When presented with a problem, data and statistical inference about a phenomenon, one needs to critically assess the validity of the assumptions, accuracy of the models and correctness of the interpretation of the thesis. There are many so called paradoxes, where one can easily be convinced by an erroneous conclusion because the underlying principles are violated (e.g., [http://en.wikipedia.org/wiki/Simpson_paradox Simpson's paradox], the [http://en.wikipedia.org/wiki/Birthday_paradox Birthday paradox], etc.) Critical evaluation of the design of the experiment, data collection, measurements and validity of the analysis strategy should lead to the correct inference and interpretation in most cases. | ||
| - | + | Suppose we stidy the success rates for treatments involving both ''small'' and ''large'' kidney stones -- treatment ''A'' includes all open procedures and treatment ''B'' is percutaneous nephrolithotomy: | |
| - | + | ||
| - | + | {| class="wikitable" summary="results accounting for stone size" style="margin-left:auto; margin-right:auto;" | |
| + | ! || Treatment A || Treatment B | ||
| + | |- | ||
| + | | Small Stones | ||
| + | | ''Group 1''<br/>'''93% (81/87)''' || ''Group 2''<br/>87% (234/270) | ||
| + | |- align="center" | ||
| + | | Large Stones | ||
| + | | ''Group 3''<br/>'''73% (192/263)''' || ''Group 4''<br/>69% (55/80) | ||
| + | |- align="center" | ||
| + | | Both | ||
| + | | 78% (273/350) || '''83% (289/350) | ||
| + | |} | ||
| - | + | The Simpson paradox shows why the conclusion that ''treatment A'' is more effective when used on small stones, and also when used on large stones, may be misinterpreted as ''treatment B'' being more effective when considering both groups jointly. | |
| - | + | ||
| - | + | In summary, one must: | |
| - | + | * be presented with a problem | |
| + | * critically analyze the given information | ||
| + | * design an experiment to collect data | ||
| + | * analyze the collection | ||
| + | * evaluate the experiment | ||
| + | * validate the inferences and interpretations made | ||
| - | + | ==Examples of Common Causes for Data Misinterpretation== | |
| - | + | ===Unrepresentative Samples=== | |
| - | === | + | These are collections of data measurement or observations that do not adequately describe the natural process or phenomenon being studied. The phrase ''garbage-in, garbage-out'' refers to this situation and implies that none of the conclusions or the inference based on such unrepresentative samples should be trusted. In general, collecting a population representative sample is a hard part of experimental design. |
| - | + | * '''Self-Selection''' - voluntary response samples, where the respondents, units or participants decide whether to be in the sample, survey or experiment. | |
| + | * ''Non-Sampling Errors'' (e.g., non-response bias) are errors in the data collection that are not due to the process of sampling or the study design. | ||
| - | * | + | ===Sampling Errors=== |
| + | Sampling errors arise from a decision of using a sample rather than measuring the entire population. | ||
| + | |||
| + | ===Samples of Small Sizes=== | ||
| + | Small sample sizes may significantly distort the interpretation of the data, or results, because a small-sample data [[EBook#Chapter_II:_Describing.2C_Exploring.2C_and_Comparing_Data | distribution may have completely different characteristics]] from the native population where the sample is drawn from (e.g., center, spread, shape, etc.) For example, use the [[SOCR_EduMaterials_Activities_GeneralCentralLimitTheorem | SOCR CLT activity]] to sample small samples from varieties of distributions and compare the sample-histogram against the population distribution. Their characteristics will be mostly similar, but sometimes drastically different. | ||
| + | |||
| + | ===Loaded Questions in Surveys or Polls=== | ||
| + | The phrasing of questions, their intonation and emphasis may significantly affect the perception of the question (intentionally or unintentionally). | ||
| + | |||
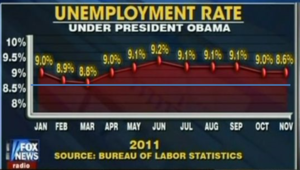
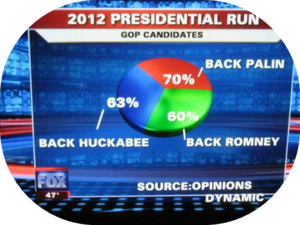
| + | ===Misleading Graphs=== | ||
| + | Look at the quantitative information represented in a chart or plot, not at the shape, orientation, relation or pattern represented by the graph. | ||
| + | * Partial Pictures | ||
| + | * Deliberate Distortions | ||
| + | * Scale breaks and axes scaling | ||
| + | <center>[[Image:EBook_IntroUses_Misleading_Graphs_F1.png|300px]] | ||
| + | [[Image:EBook_IntroUses_Misleading_Graphs_F2.png|300px]] | ||
| + | [[Image:EBook_IntroUses_Misleading_Graphs_F3.png|300px]] | ||
| + | [[Image:EBook_IntroUses_Misleading_Graphs_F4.png|300px]] | ||
| + | </center> | ||
| + | |||
| + | See [http://www.bbc.co.uk/schools/gcsebitesize/maths/statistics/representingdata2rev5.shtml more examples here]. | ||
| + | |||
| + | ===Inappropriate estimates or statistics=== | ||
| + | Erroneous population parameter estimates (intentionally or most likely unintentionally) may affect data collections. The source of the data and the method for parameter estimation should be carefully reviewed to avoid bias and misinterpretation of data, results and to guarantee robust inference. | ||
| + | |||
| + | ==Computational Resources: Internet-based SOCR Tools== | ||
| + | * [http://www.socr.ucla.edu/htmls/SOCR_Experiments.html SOCR Experiments] | ||
| + | * [http://www.socr.ucla.edu/htmls/SOCR_Charts.html SOCR Charts] | ||
| + | |||
| + | ==Examples & Hands-on Activities== | ||
| + | * [[SOCR_EduMaterials_Activities_BirthdayExperiment | Birthday Paradox I]] | ||
| + | * [[SOCR_EduMaterials_Activities_Birthday | Birthday Paradox II]] | ||
| + | |||
| + | ==[[EBook_Problems_EDA_IntroUses|Problems]]== | ||
<hr> | <hr> | ||
| - | + | ==References== | |
| - | * | + | * [[SOCR_Quotes | SOCR Quotes]] |
<hr> | <hr> | ||
Current revision as of 15:35, 3 April 2013
General Advance-Placement (AP) Statistics Curriculum - Uses and Abuses of Statistics
Contents |
Uses and Abuses of Statistics
Statistics is the science of variation, randomness and chance. As such, statistics is different from the Newtonian sciences, where the processes being studied obey exact deterministic mathematical laws and typically can be described as systems. Since statistics provides tools for data understanding where no other science can, one should be prepared to treat this new power of knowledge with uncertainty. In general, statistical analysis, inference and simulation will not provide deterministic answers and strict (e.g., yes/no, presence/absence) responses to questions involving stochastic processes. Rather, statistics will provide quantitative inference represented as long-time probability values, confidence or prediction intervals, odds, chances, etc., which may ultimately be subjected to varyious interpretations.
This possibility of multiple interpretations may be viewed by some as detrimental or inconsistent. However, some others may consider these outcomes as beautiful, scientific and elegant responses to challenging problems that are inherently stochastic. The phrase Uses and Abuses of Statistics refers to the notion that in some cases statistical results may be used as evidence to seemingly opposite these. However, most of the time, common principles of logic allow us to disambiguate the obtained statistical inference. Some appropriate probability and statistics quotes are provided in the references section.
Approach
When presented with a problem, data and statistical inference about a phenomenon, one needs to critically assess the validity of the assumptions, accuracy of the models and correctness of the interpretation of the thesis. There are many so called paradoxes, where one can easily be convinced by an erroneous conclusion because the underlying principles are violated (e.g., Simpson's paradox, the Birthday paradox, etc.) Critical evaluation of the design of the experiment, data collection, measurements and validity of the analysis strategy should lead to the correct inference and interpretation in most cases.
Suppose we stidy the success rates for treatments involving both small and large kidney stones -- treatment A includes all open procedures and treatment B is percutaneous nephrolithotomy:
| Treatment A | Treatment B | |
|---|---|---|
| Small Stones | Group 1 93% (81/87) | Group 2 87% (234/270) |
| Large Stones | Group 3 73% (192/263) | Group 4 69% (55/80) |
| Both | 78% (273/350) | 83% (289/350) |
The Simpson paradox shows why the conclusion that treatment A is more effective when used on small stones, and also when used on large stones, may be misinterpreted as treatment B being more effective when considering both groups jointly.
In summary, one must:
- be presented with a problem
- critically analyze the given information
- design an experiment to collect data
- analyze the collection
- evaluate the experiment
- validate the inferences and interpretations made
Examples of Common Causes for Data Misinterpretation
Unrepresentative Samples
These are collections of data measurement or observations that do not adequately describe the natural process or phenomenon being studied. The phrase garbage-in, garbage-out refers to this situation and implies that none of the conclusions or the inference based on such unrepresentative samples should be trusted. In general, collecting a population representative sample is a hard part of experimental design.
- Self-Selection - voluntary response samples, where the respondents, units or participants decide whether to be in the sample, survey or experiment.
- Non-Sampling Errors (e.g., non-response bias) are errors in the data collection that are not due to the process of sampling or the study design.
Sampling Errors
Sampling errors arise from a decision of using a sample rather than measuring the entire population.
Samples of Small Sizes
Small sample sizes may significantly distort the interpretation of the data, or results, because a small-sample data distribution may have completely different characteristics from the native population where the sample is drawn from (e.g., center, spread, shape, etc.) For example, use the SOCR CLT activity to sample small samples from varieties of distributions and compare the sample-histogram against the population distribution. Their characteristics will be mostly similar, but sometimes drastically different.
Loaded Questions in Surveys or Polls
The phrasing of questions, their intonation and emphasis may significantly affect the perception of the question (intentionally or unintentionally).
Misleading Graphs
Look at the quantitative information represented in a chart or plot, not at the shape, orientation, relation or pattern represented by the graph.
- Partial Pictures
- Deliberate Distortions
- Scale breaks and axes scaling

See more examples here.
Inappropriate estimates or statistics
Erroneous population parameter estimates (intentionally or most likely unintentionally) may affect data collections. The source of the data and the method for parameter estimation should be carefully reviewed to avoid bias and misinterpretation of data, results and to guarantee robust inference.
Computational Resources: Internet-based SOCR Tools
Examples & Hands-on Activities
Problems
References
- SOCR Home page: http://www.socr.ucla.edu
Translate this page: