AP Statistics Curriculum 2007 Johnson SB
From Socr
Contents |
General Advance-Placement (AP) Statistics Curriculum - Johnson SB Distribution
Johnson SB Distribution
The Johnson SB distribution is related to the normal distribution. Four parameters are needed: Γ, δ, λ, ε . It is a continuous distribution defined on bounded range 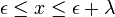 , and the distribution can be symmetric or asymmetric.
, and the distribution can be symmetric or asymmetric.
PDF:
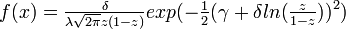 , where
, where 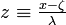
CDF:
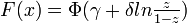 , where
, where 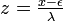
Moments:
Moments for this distribution do not have a simple expression.
Applications
 Epidemiology: http://www.bvsde.paho.org/bvsacd/cd47/data.pdf
Epidemiology: http://www.bvsde.paho.org/bvsacd/cd47/data.pdf
 Forrestry: http://cms1.gre.ac.uk/conferences/iufro/FMA/SB_Plot_Minimum1.pdf
Forrestry: http://cms1.gre.ac.uk/conferences/iufro/FMA/SB_Plot_Minimum1.pdf
SOCR Links
http://www.distributome.org/ -> SOCR -> Distributions -> Johnson Special Bounded (SB) Distribution
http://www.distributome.org/ -> SOCR -> Functors -> Johnson Special Bounded (SB) Distribution
SOCR Docs: http://www.socr.ucla.edu/docs/edu/ucla/stat/SOCR/distributions/JohnsonSBDistribution.html
SOCR Calculator: http://socr.ucla.edu/htmls/dist/JohnsonSBDistribution.html
See Also
http://www.mathwave.com/articles/johnson_sb_distribution.html
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:
