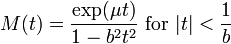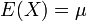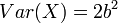AP Statistics Curriculum 2007 Laplace
From Socr
(→Laplace Distribution) |
(→Related Distributions) |
||
| Line 43: | Line 43: | ||
*If <math>X\sim Laplace(\mu,b)\!</math>, then <math>kX+b\sim Laplace(k\mu+b,kb)\!</math> | *If <math>X\sim Laplace(\mu,b)\!</math>, then <math>kX+b\sim Laplace(k\mu+b,kb)\!</math> | ||
*If <math>X \sim Laplace(0,b)\!</math>, then <math>|X| \sim Exponential(\tfrac{1}{b})\!</math> ([[exponential distribution]]) | *If <math>X \sim Laplace(0,b)\!</math>, then <math>|X| \sim Exponential(\tfrac{1}{b})\!</math> ([[exponential distribution]]) | ||
| - | |||
| - | |||
| - | |||
===Applications=== | ===Applications=== | ||
Revision as of 21:01, 11 July 2011
Laplace Distribution
Definition: Laplace distribution is a distribution that is symmetrical and more “peaky” than a normal distribution. The dispersion of the data around the mean is higher than that of a normal distribution. Laplace distribution is also sometimes called the double exponential distribution.
Probability density function: For X~Laplace(μ,b), the Laplace probability density function is given by
where
- e is the natural number (e = 2.71828…)
- b is a scale parameter (determines the profile of the distribution)
- μ is the mean
- x is a random variable
Cumulative density function: The Laplace cumulative distribution function is given by
where
- e is the natural number (e = 2.71828…)
- b is a scale parameter (determines the profile of the distribution)
- μ is the mean
- x is a random variable
Moment generating function: The Laplace moment-generating function is
Expectation:
Variance: The gamma variance is
Related Distributions
- If
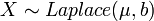 , then
, then 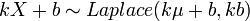
- If
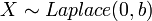 , then
, then 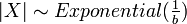 (exponential distribution)
(exponential distribution)
Applications
The Laplace distribution is used for modeling in signal processing, various biological processes, finance, and economics. Examples of events that may be modeled by Laplace distribution include:
- Credit risk and exotic options in financial engineering
- Insurance claims
- Structural changes in switching-regime model and Kalman filter
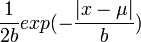
![\left\{\begin{matrix}
\frac{1}{2}\exp(\frac{x-\mu}{b}) & \mbox{if }x < \mu
\\[8pt]
1-\frac{1}{2}\exp(-\frac{x-\mu}{b}) & \mbox{if }x \geq \mu
\end{matrix}\right.](/socr/uploads/math/6/b/e/6be820c4b4bb39a40b48397c84bc8617.png)