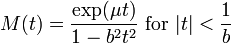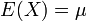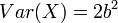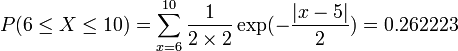AP Statistics Curriculum 2007 Laplace
From Socr
(→Related Distributions) |
(→Applications) |
||
| Line 49: | Line 49: | ||
*Insurance claims | *Insurance claims | ||
*Structural changes in switching-regime model and Kalman filter | *Structural changes in switching-regime model and Kalman filter | ||
| + | |||
| + | ===Example=== | ||
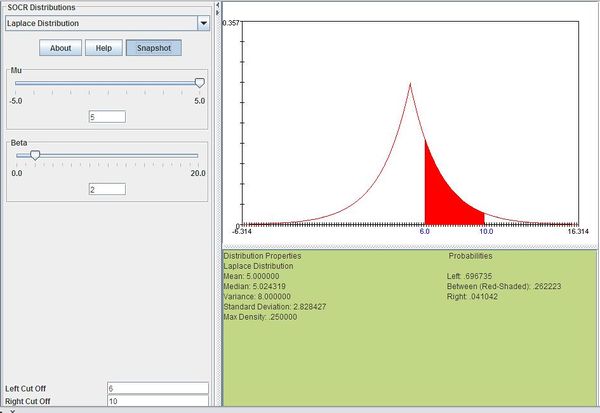
| + | Suppose that the return of a certain stock has a Laplace distribution with <font size=3><math>\mu=5</math></font> and <font size=3><math>b=2</math></font>. Compute the probability that the stock will have a return between 6 and 10. | ||
| + | |||
| + | We can compute this as follows: | ||
| + | |||
| + | :<math>P(6 \le X\le 10)=\sum_{x=6}^{10}\frac{1}{2\times 2}\exp(-\frac{|x-5|}{2})=0.262223</math> | ||
| + | |||
| + | The figure below shows this result using [http://socr.ucla.edu/htmls/dist/Laplace_Distribution.html SOCR distributions] | ||
| + | <center>[[Image:Laplace.jpg|600px]]</center> | ||
Revision as of 21:07, 11 July 2011
Contents |
Laplace Distribution
Definition: Laplace distribution is a distribution that is symmetrical and more “peaky” than a normal distribution. The dispersion of the data around the mean is higher than that of a normal distribution. Laplace distribution is also sometimes called the double exponential distribution.
Probability density function: For X~Laplace(μ,b), the Laplace probability density function is given by
where
- e is the natural number (e = 2.71828…)
- b is a scale parameter (determines the profile of the distribution)
- μ is the mean
- x is a random variable
Cumulative density function: The Laplace cumulative distribution function is given by
where
- e is the natural number (e = 2.71828…)
- b is a scale parameter (determines the profile of the distribution)
- μ is the mean
- x is a random variable
Moment generating function: The Laplace moment-generating function is
Expectation:
Variance: The gamma variance is
Related Distributions
- If
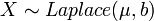 , then
, then 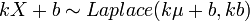
- If
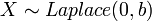 , then
, then 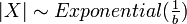 (exponential distribution)
(exponential distribution)
Applications
The Laplace distribution is used for modeling in signal processing, various biological processes, finance, and economics. Examples of events that may be modeled by Laplace distribution include:
- Credit risk and exotic options in financial engineering
- Insurance claims
- Structural changes in switching-regime model and Kalman filter
Example
Suppose that the return of a certain stock has a Laplace distribution with μ = 5 and b = 2. Compute the probability that the stock will have a return between 6 and 10.
We can compute this as follows:
The figure below shows this result using SOCR distributions
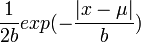
![\left\{\begin{matrix}
\frac{1}{2}\exp(\frac{x-\mu}{b}) & \mbox{if }x < \mu
\\[8pt]
1-\frac{1}{2}\exp(-\frac{x-\mu}{b}) & \mbox{if }x \geq \mu
\end{matrix}\right.](/socr/uploads/math/6/b/e/6be820c4b4bb39a40b48397c84bc8617.png)