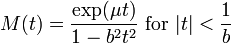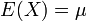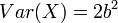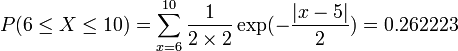AP Statistics Curriculum 2007 Laplace
From Socr
Contents |
Laplace Distribution
Definition: Laplace distribution is a distribution that is symmetrical and more “peaky” than a normal distribution. The dispersion of the data around the mean is higher than that of a normal distribution. Laplace distribution is also sometimes called the double exponential distribution.
Probability density function: For X~Laplace(μ,b), the Laplace probability density function is given by
where
- e is the natural number (e = 2.71828…)
- b is a scale parameter (determines the profile of the distribution)
- μ is the mean
- x is a random variable
Cumulative density function: The Laplace cumulative distribution function is given by
where
- e is the natural number (e = 2.71828…)
- b is a scale parameter (determines the profile of the distribution)
- μ is the mean
- x is a random variable
Moment generating function: The Laplace moment-generating function is
Expectation:
Variance: The gamma variance is
Related Distributions
- If
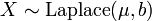 , then
, then 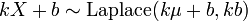
- If
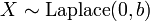 , then
, then 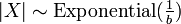 (Exponential distribution)
(Exponential distribution)
- If
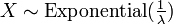 and
and 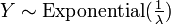 , then
, then 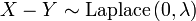
- If
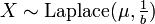 , then
, then 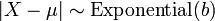
- If
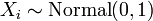 for
for 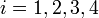 then
then 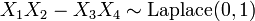 (Normal distribution)
(Normal distribution)
- If
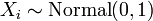 for
for 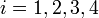 , then
, then 
- If
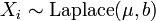 , then
, then 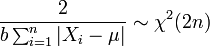 (Chi-square distribution)
(Chi-square distribution)
- If
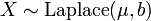 and
and 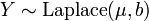 then
then 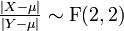 (F-distribution)
(F-distribution)
Applications
The Laplace distribution is used for modeling in signal processing, various biological processes, finance, and economics. Examples of events that may be modeled by Laplace distribution include:
- Credit risk and exotic options in financial engineering
- Insurance claims
- Structural changes in switching-regime model and Kalman filter
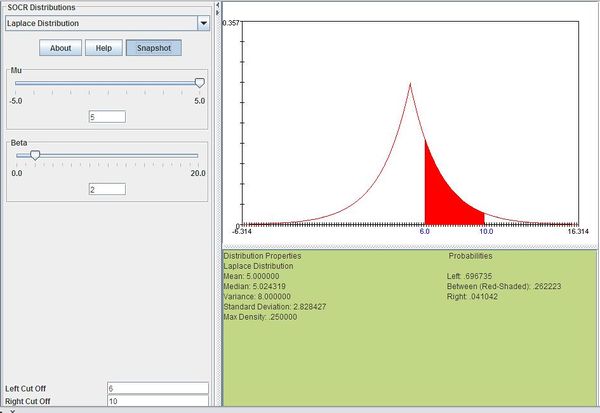
Example
Suppose that the return of a certain stock has a Laplace distribution with μ = 5 and b = 2. Compute the probability that the stock will have a return between 6 and 10.
We can compute this as follows:
The figure below shows this result using SOCR distributions
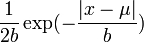
![\left\{\begin{matrix}
\frac{1}{2}\exp(\frac{x-\mu}{b}) & \mbox{if }x < \mu
\\[8pt]
1-\frac{1}{2}\exp(-\frac{x-\mu}{b}) & \mbox{if }x \geq \mu
\end{matrix}\right.](/socr/uploads/math/6/b/e/6be820c4b4bb39a40b48397c84bc8617.png)