AP Statistics Curriculum 2007 Limits LLN
From Socr
m (→See also: typo) |
m (→SOCR LLN Activity) |
||
| Line 17: | Line 17: | ||
The [[SOCR_EduMaterials_Activities_LawOfLargeNumbers | complete SOCR LLN Activity is available here]]. | The [[SOCR_EduMaterials_Activities_LawOfLargeNumbers | complete SOCR LLN Activity is available here]]. | ||
| - | Go to [http://socr.ucla.edu/htmls/ | + | Go to [http://socr.ucla.edu/htmls/exp/Coin_Toss_LLN_Experiment.html SOCR Experiments] and select the '''Coin Toss LLN Experiment''' from the drop-down list of experiments in the top-left panel. This applet consists of a control toolbar on the top followed by a graph panel in the middle and a results table at the bottom. Use the toolbar to flip coins one at a time, 10, 100, 1,000 at a time or continuously! The toolbar also allows you to stop or reset an experiment and select the probability of Heads ('''p''') using the slider. The graph panel in the middle will dynamically plot the values of the two variables of interest (''proportion of heads'' and ''difference of Heads and Tails''). The outcome table at the bottom presents the summaries of all trials of this experiment. |
===LLN Application=== | ===LLN Application=== | ||
Revision as of 16:42, 17 February 2012
Contents |
General Advance-Placement (AP) Statistics Curriculum - The Law of Large Numbers
Motivation
Suppose we independently conduct one experiment repeatedly. Assume that we are interested in the relative frequency of the occurrence of one event whose probability to be observed at each experiment is p. The ratio of the observed frequency of that event to the total number of repetitions converges towards p as the number of (identical and independent) experiments increases. This is an informal statement of the Law of Large Numbers (LLN).
For a more concrete example, suppose we study the average height of a class of 100 students. Compared to the average height of 3 randomly chosen students from this class, the average height of 10 randomly chosen students is most likely closer to the real average height of all 100 students. Since the sample of 10 is a larger than the sample of 3, it is a better representation of the entire class. At one extreme, a sample of 99 of the 100 students will produce a sample average height almost exactly the same as the average height for all 100 students. On the other extreme, sampling a single student will be an extremely variant estimate of the overall class average weight.
The Law of Large Numbers (LLN)
The complete formal statements of the LLN are discussed here.
It is generally necessary to draw the parallels between the formal LLN statements (in terms of sample averages) and the frequent interpretations of the LLN (in terms of probabilities of various events).
Suppose we observe the same process independently multiple times. Assume a binarized (dichotomous) function of the outcome of each trial is of interest (e.g., failure may denote the event that the continuous voltage measure < 0.5V, and the complement, success, that voltage ≥ 0.5V – this is the situation in electronic chips which binarize electric currents to 0 or 1). Researchers are often interested in the event of observing a success at a given trial or the number of successes in an experiment consisting of multiple trials. Let’s denote p=P(success) at each trial. Then, the ratio of the total number of successes to the number of trials (n) is the average 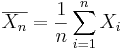 , where
, where 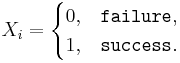 represents the outcome of the ith trial. Thus,
represents the outcome of the ith trial. Thus, 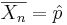 , the ratio of the observed frequency of that event to the total number of repetitions, estimates the true p=P(success). Therefore,
, the ratio of the observed frequency of that event to the total number of repetitions, estimates the true p=P(success). Therefore, 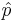 converges towards p as the number of (identical and independent) trials increases.
converges towards p as the number of (identical and independent) trials increases.
SOCR LLN Activity
The complete SOCR LLN Activity is available here.
Go to SOCR Experiments and select the Coin Toss LLN Experiment from the drop-down list of experiments in the top-left panel. This applet consists of a control toolbar on the top followed by a graph panel in the middle and a results table at the bottom. Use the toolbar to flip coins one at a time, 10, 100, 1,000 at a time or continuously! The toolbar also allows you to stop or reset an experiment and select the probability of Heads (p) using the slider. The graph panel in the middle will dynamically plot the values of the two variables of interest (proportion of heads and difference of Heads and Tails). The outcome table at the bottom presents the summaries of all trials of this experiment.
LLN Application
One demonstration of the law of large numbers provides practical algorithms for estimation of transcendental numbers. The two most popular transcendental numbers are π and e.
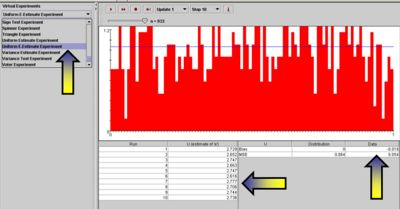
The SOCR E-Estimate Experiment provides the complete details of this simulation. In a nutshell, we can estimate the value of the natural number e using random sampling from Uniform distribution. Suppose 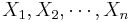 are drawn from Uniform distribution on (0, 1) and define
are drawn from Uniform distribution on (0, 1) and define 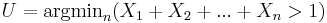 , note that all
, note that all 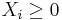 .
.
Now, the expected value 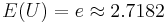 . Therefore, by LLN, taking averages of
. Therefore, by LLN, taking averages of 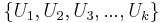 values, each computed from random samples
values, each computed from random samples 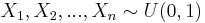 as described above, will provide a more accurate estimate (as
as described above, will provide a more accurate estimate (as 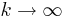 ) of the natural number e.
) of the natural number e.
The Uniform E-Estimate Experiment, part of SOCR Experiments, provides a hands-on demonstration of how the LLN facilitates stochastic simulation-based estimation of e.
See also
- The SOCR Law of Large Numbers Activity
- Estimating π using SOCR simulation
- Simple LLN Experiment Applet
- Coin Toss LLN Experiment Applet
Problems
References
- Dinov, ID, Christou, N, and Gould, R (2009) Law of Large Numbers: the Theory, Applications and Technology-based Education. JSE, Vol. 17, No. 1, 1-15, 2009.
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:
