AP Statistics Curriculum 2007 Limits Norm2Bin
From Socr
(→Normal Approximation to Binomial Distribution) |
m (→Normal Approximation to Binomial Distribution) |
||
| (12 intermediate revisions not shown) | |||
| Line 2: | Line 2: | ||
=== Normal Approximation to Binomial Distribution=== | === Normal Approximation to Binomial Distribution=== | ||
| - | Suppose [[AP_Statistics_Curriculum_2007_Distrib_Binomial | <math>Y | + | Suppose [[AP_Statistics_Curriculum_2007_Distrib_Binomial | <math>Y\sim Binomial(n, p)</math>]] and <math>Y=Y_1+ Y_2+ Y_3+\cdots+ Y_n</math>, where [[AP_Statistics_Curriculum_2007_Distrib_Binomial | <math>Y_k \sim Bernoulli(p)</math>]] , <math>E(Y_k)=p</math> & <math>Var(Y_k)=p(1-p)</math>. Then <math>E(Y)=np</math>, <math>Var(Y)=np(1-p)</math> and <math>SD(Y)= \sqrt{np(1-p)}</math>. If we use the [[AP_Statistics_Curriculum_2007_Normal_Prob | Normal Standardization formula]] for ''Y'' we get <math>Z={Y-np\over \sqrt{np(1-p)}}</math>. |
| - | By [[AP_Statistics_Curriculum_2007_Limits_CLT | CLT]], <math>Z \sim N(0, 1)</math> and <math>Y \sim N [\mu=np, \sigma^2={np(1-p) | + | By [[AP_Statistics_Curriculum_2007_Limits_CLT | CLT]], <math>Z \sim N(0, 1)</math> and <math>Y \sim N [\mu=np, \sigma^2={np(1-p)}]</math>. |
* Note: Normal approximation to Binomial is reasonable when ''p'' and ''(1-p)'' are NOT too small relative to n: | * Note: Normal approximation to Binomial is reasonable when ''p'' and ''(1-p)'' are NOT too small relative to n: | ||
: <math>np\geq 10</math> | : <math>np\geq 10</math> | ||
| - | : <math>n(1-p)>10</math> | + | : <math>n(1-p)> 10</math> |
| + | |||
| + | * Note that the conditions of [[AP_Statistics_Curriculum_2007_Normal_Prob | Normal]] approximation to [[AP_Statistics_Curriculum_2007_Distrib_Binomial | Binomial]] are complementary to the [[AP_Statistics_Curriculum_2007_Limits_Poisson2Bin | conditions for Poisson approximation of Binomial distribution]]. | ||
===Example=== | ===Example=== | ||
| - | The [[SOCR_EduMaterials_Activities_RouletteExperiment | Roulette Game]] has 38 slots | + | The [[SOCR_EduMaterials_Activities_RouletteExperiment | Roulette Game]] has 38 slots: 18 red, 18 black and 2 neutral. Suppose we play 100 games betting on red each time. Would observing 58 wins in the 100 games be considered atypical (suspicious)? |
To answer this question, we need to compute the probability <math>P(Y\geq58)</math>, where <math>Y\sim Binomial(100, 0.47)</math>, as ''P(Win)=P(Red outcome) = 18/38=0.47''. | To answer this question, we need to compute the probability <math>P(Y\geq58)</math>, where <math>Y\sim Binomial(100, 0.47)</math>, as ''P(Win)=P(Red outcome) = 18/38=0.47''. | ||
| - | Since <math>np=47 \geq 10</math> and <math>n(1-p)=53>10</math>, Normal approximation is justified. Let <math>Z=(Y-np)\over \sqrt{np(1-p)} =(58-100*0.47)\sqrt | + | Since <math>np=47 \geq 10</math> and <math>n(1-p)=53>10</math>, Normal approximation is justified. Let <math>Z={(Y-np)\over \sqrt{np(1-p)}} ={(58-100*0.47)\over \sqrt{100*0.47*0.53}}=2.2</math>. Thus we can '''approximate''' <math>P(Y\geq 58) \approx P(Z\geq 2.2) = 0.0139</math>. The last equation can be directly computed using the [http://socr.ucla.edu/htmls/SOCR_Distributions.html SOCR Normal Distribution Calculator]. You can also use the [http://socr.ucla.edu/htmls/SOCR_Distributions.html SOCR Binomial Distribution Calculator] to compute the '''exact probability''' <math>P(Y\geq 58) = 0.0177</math>. |
| - | So why is the [[AP_Statistics_Curriculum_2007_Normal_Std Normal]] approximation to [[AP_Statistics_Curriculum_2007_Distrib_Binomial | Binomial]] distribution necessary in practice? | + | So why is the [[AP_Statistics_Curriculum_2007_Normal_Std | Normal]] approximation to [[AP_Statistics_Curriculum_2007_Distrib_Binomial | Binomial]] distribution necessary in practice? |
Binomial approximation by Normal distribution is useful when no access to the online SOCR resources is available (but we can use printed version of the [http://socr.ucla.edu/Applets.dir/Z-table.html Normal Table] or when N is large and binomial probabilities are difficult to compute precisely! | Binomial approximation by Normal distribution is useful when no access to the online SOCR resources is available (but we can use printed version of the [http://socr.ucla.edu/Applets.dir/Z-table.html Normal Table] or when N is large and binomial probabilities are difficult to compute precisely! | ||
| Line 36: | Line 38: | ||
But we can also ''approximate'' this probability using the normal distribution. We will need the mean and the standard deviation of this [[About_pages_for_SOCR_Distributions | normal distribution]]. These are | But we can also ''approximate'' this probability using the normal distribution. We will need the mean and the standard deviation of this [[About_pages_for_SOCR_Distributions | normal distribution]]. These are | ||
<math> \mu=np=80\frac{4}{52}=6.154 </math> and | <math> \mu=np=80\frac{4}{52}=6.154 </math> and | ||
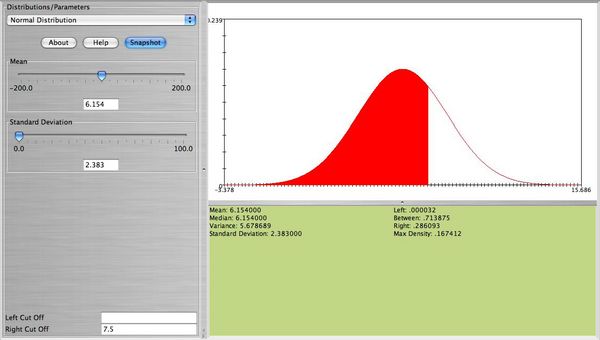
| - | <math> \sigma=\sqrt{80 \frac{4}{52}\frac{48}{52}}=2.383. </math> Of course this can be obtained directly from the SOCR Binomial applet. Now, all you need to do is to select the SOCR normal distribution applet and enter for the mean 6.154, and for the standard deviation 2.383. To obtain the desire probability in the right cut-off box enter 7.5 (using the continuity correction for better approximation). The approximate probability is <math> P(X \ge 8) \approx 0.2861 </math> (see figure below). | + | <math> \sigma=\sqrt{80 \frac{4}{52}\frac{48}{52}}=2.383. </math> Of course this can be obtained directly from the SOCR Binomial applet. Now, all you need to do is to select the SOCR normal distribution applet and enter for the mean 6.154, and for the standard deviation 2.383. To obtain the desire probability in the right cut-off box, enter 7.5 (using the continuity correction for better approximation). The approximate probability is <math> P(X \ge 8) \approx 0.2861 </math> (see figure below). |
<center>[[Image: SOCR_Activities_ExploreDistributions_Christou_figure10.jpg|600px]]</center> | <center>[[Image: SOCR_Activities_ExploreDistributions_Christou_figure10.jpg|600px]]</center> | ||
<hr> | <hr> | ||
| - | === | + | |
| + | ===[[EBook_Problems_Limits_Norm2Bin|Problems]]=== | ||
<hr> | <hr> | ||
Current revision as of 02:40, 12 February 2011
Contents |
General Advance-Placement (AP) Statistics Curriculum - Normal Distribution as Approximation to Binomial Distribution
Normal Approximation to Binomial Distribution
Suppose 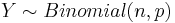 and
and 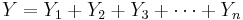 , where Yk˜Bernoulli(p) , E(Yk) = p & Var(Yk) = p(1 − p). Then E(Y) = np, Var(Y) = np(1 − p) and
, where Yk˜Bernoulli(p) , E(Yk) = p & Var(Yk) = p(1 − p). Then E(Y) = np, Var(Y) = np(1 − p) and 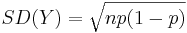 . If we use the Normal Standardization formula for Y we get
. If we use the Normal Standardization formula for Y we get 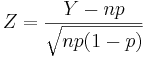 .
.
By CLT, 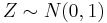 and
and ![Y \sim N [\mu=np, \sigma^2={np(1-p)}]](/socr/uploads/math/9/7/5/9759b2a301e62c518f679e38c205757e.png) .
.
- Note: Normal approximation to Binomial is reasonable when p and (1-p) are NOT too small relative to n:
-
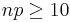
- n(1 − p) > 10
- Note that the conditions of Normal approximation to Binomial are complementary to the conditions for Poisson approximation of Binomial distribution.
Example
The Roulette Game has 38 slots: 18 red, 18 black and 2 neutral. Suppose we play 100 games betting on red each time. Would observing 58 wins in the 100 games be considered atypical (suspicious)?
To answer this question, we need to compute the probability 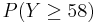 , where
, where 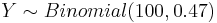 , as P(Win)=P(Red outcome) = 18/38=0.47.
, as P(Win)=P(Red outcome) = 18/38=0.47.
Since 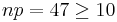 and n(1 − p) = 53 > 10, Normal approximation is justified. Let
and n(1 − p) = 53 > 10, Normal approximation is justified. Let 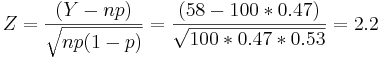 . Thus we can approximate
. Thus we can approximate 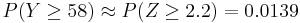 . The last equation can be directly computed using the SOCR Normal Distribution Calculator. You can also use the SOCR Binomial Distribution Calculator to compute the exact probability
. The last equation can be directly computed using the SOCR Normal Distribution Calculator. You can also use the SOCR Binomial Distribution Calculator to compute the exact probability 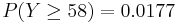 .
.
So why is the Normal approximation to Binomial distribution necessary in practice?
Binomial approximation by Normal distribution is useful when no access to the online SOCR resources is available (but we can use printed version of the Normal Table or when N is large and binomial probabilities are difficult to compute precisely!
Activities
Graph and comment on the shape of binomial with n = 20,p = 0.1 and n = 20,p = 0.9. Now, keep n = 20 but change p = 0.45. What do you observe now? How about when n = 80,p = 0.1. See the four figures below.
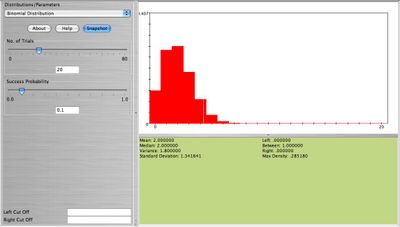
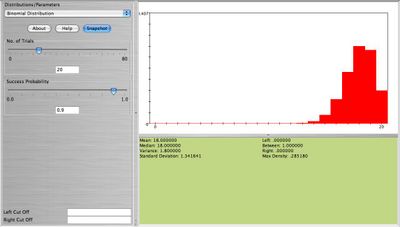
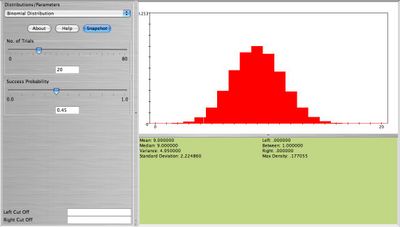
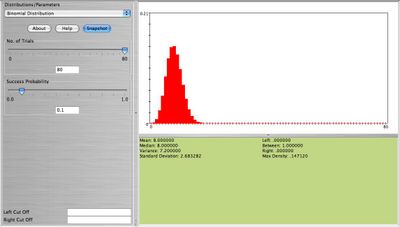
What is your conclusion on the shape of the Binomial distribution in relation to its parameters n,p? Clearly when n is large and p small or large the result is a bell-shaped distribution. When n is small (10-20) we still get approximately a bell-shaped distribution as long as 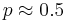 . Because of this feature of the Binomial distribution we can approximate Binomial distributions using the normal distribution when the above requirements hold. Here is one example: Eighty cards are drawn with replacement from the standard 52-card deck. Find the exact probability that at least 8 aces are obtained. This can be computed using the formula
. Because of this feature of the Binomial distribution we can approximate Binomial distributions using the normal distribution when the above requirements hold. Here is one example: Eighty cards are drawn with replacement from the standard 52-card deck. Find the exact probability that at least 8 aces are obtained. This can be computed using the formula
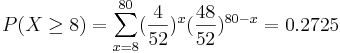 .
.
Much easier we can use SOCR to compute this probability (see figure below).
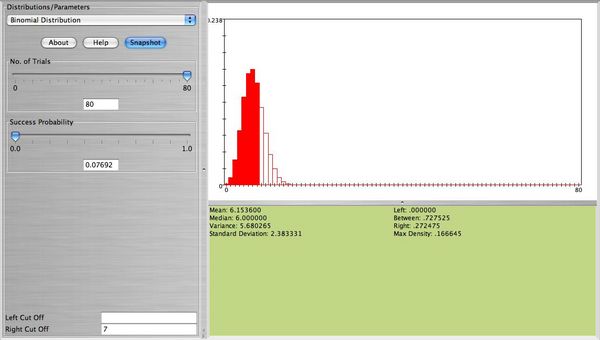
But we can also approximate this probability using the normal distribution. We will need the mean and the standard deviation of this normal distribution. These are
 and
and
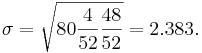 Of course this can be obtained directly from the SOCR Binomial applet. Now, all you need to do is to select the SOCR normal distribution applet and enter for the mean 6.154, and for the standard deviation 2.383. To obtain the desire probability in the right cut-off box, enter 7.5 (using the continuity correction for better approximation). The approximate probability is
Of course this can be obtained directly from the SOCR Binomial applet. Now, all you need to do is to select the SOCR normal distribution applet and enter for the mean 6.154, and for the standard deviation 2.383. To obtain the desire probability in the right cut-off box, enter 7.5 (using the continuity correction for better approximation). The approximate probability is 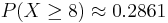 (see figure below).
(see figure below).
Problems
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:
