AP Statistics Curriculum 2007 Limits Norm2Poisson
From Socr
(added see also and Applications: Positron Emission Tomography sections) |
(→Examples) |
||
| (One intermediate revision not shown) | |||
| Line 13: | Line 13: | ||
<center>[[Image: SOCR_Activities_ExploreDistributions_Christou_figure11.jpg|600px]]</center> | <center>[[Image: SOCR_Activities_ExploreDistributions_Christou_figure11.jpg|600px]]</center> | ||
| - | * '''Note''': We observe that this distribution is bell-shaped. We can use the normal distribution to approximate this probability. Using <math> N(\mu=50, \sigma=\sqrt{50}=7.071) </math>, together with the continuity correction for better approximation we obtain | + | * '''Note''': We observe that this distribution is bell-shaped. We can use the normal distribution to approximate this probability. Using <math> N(\mu=50, \sigma=\sqrt{50}=7.071) </math>, together with the continuity correction for better approximation we obtain \(P(53.5<X<62.5| N(μ=50,σ=7.071))= 0.271759 \), which is close to the exact that was found earlier. The figure below shows this probability using the [http://socr.ucla.edu/htmls/SOCR_Distributions.html SOCR Normal Distribution Applet]. |
<center>[[Image: SOCR_Activities_ExploreDistributions_Christou_figure12.jpg|600px]]</center> | <center>[[Image: SOCR_Activities_ExploreDistributions_Christou_figure12.jpg|600px]]</center> | ||
Current revision as of 13:43, 18 September 2014
Contents |
General Advance-Placement (AP) Statistics Curriculum - Normal Approximation to Poisson Distribution
Normal Approximation to Poisson Distribution
The Poisson(λ) Distribution can be approximated with Normal when λ is large.
For sufficiently large values of λ, (say λ>1,000), the Normal(μ = λ,σ2 = λ) Distribution is an excellent approximation to the Poisson(λ) Distribution. If λ is greater than about 10, then the Normal Distribution is a good approximation if an appropriate continuity correction is performed.
If xo is a non-negative integer, 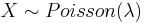 and
and 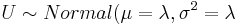 ), then PX(X < xo) = PU(U < xo + 0.5).
), then PX(X < xo) = PU(U < xo + 0.5).
Examples
Suppose cars arrive at a parking lot at a rate of 50 per hour. Let’s assume that the process is a Poisson random variable with λ = 50. Compute the probability that in the next hour the number of cars that arrive at this parking lot will be between 54 and 62. We can compute this as follows:
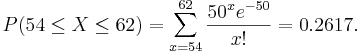 The figure below from the SOCR Poisson Distribution shows this probability.
The figure below from the SOCR Poisson Distribution shows this probability.
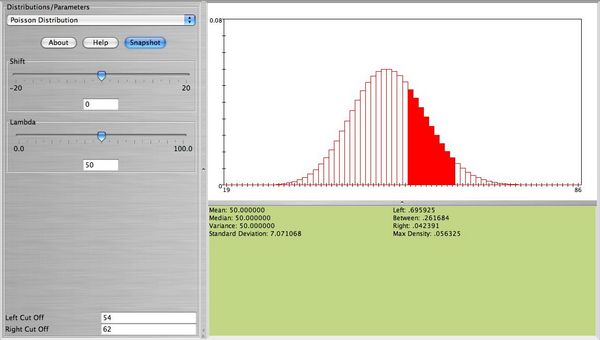
- Note: We observe that this distribution is bell-shaped. We can use the normal distribution to approximate this probability. Using
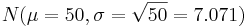 , together with the continuity correction for better approximation we obtain \(P(53.5<X<62.5| N(μ=50,σ=7.071))= 0.271759 \), which is close to the exact that was found earlier. The figure below shows this probability using the SOCR Normal Distribution Applet.
, together with the continuity correction for better approximation we obtain \(P(53.5<X<62.5| N(μ=50,σ=7.071))= 0.271759 \), which is close to the exact that was found earlier. The figure below shows this probability using the SOCR Normal Distribution Applet.
Applications: Positron Emission Tomography
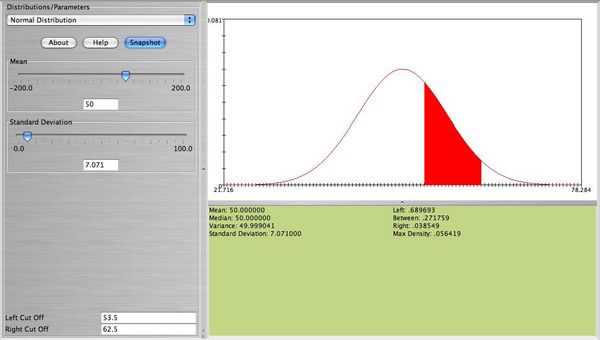
The physics of positron emission tomography (PET) provides evidence that the Poisson distribution model may be used to study the process of radioactive decay using positron emission. As tracer isotopes decay, they give off positively charged electrons which collide with negatively charged electrons the result of which (by the law of preservation of energy) is one or a pair of photons emitted at the annihilation point in space and detected by photo-multiplying tubes surrounding the imaged object (e.g., a human body part like the brain). The (large) number of arrivals at each detector is a Poisson process, which can be approximated by Normal distribution, as described above. This figure shows the schematics of the PET imaging technique.

See also
Poisson Distribution Section of the EBook.
Problems
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:
