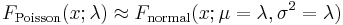AP Statistics Curriculum 2007 Limits Norm2Poisson
From Socr
(→Normal Approximation to Poisson Distribution) |
(→Normal Approximation to Poisson Distribution) |
||
| Line 4: | Line 4: | ||
The [[AP_Statistics_Curriculum_2007_Distrib_Poisson | Poisson(<math> \lambda </math>) distribution]] can be approximated with [[AP_Statistics_Curriculum_2007_Normal_Prob |Normal]] when <math> \lambda </math> is large. | The [[AP_Statistics_Curriculum_2007_Distrib_Poisson | Poisson(<math> \lambda </math>) distribution]] can be approximated with [[AP_Statistics_Curriculum_2007_Normal_Prob |Normal]] when <math> \lambda </math> is large. | ||
| - | For sufficiently large values of λ, (say λ>1,000), the [[AP_Statistics_Curriculum_2007_Normal_Prob |Normal(<math>\mu=\lambda, \sigma^2=\lambda</math>]] distribution is an excellent approximation to the Poisson distribution. If λ is greater than about 10, then the normal distribution is a good approximation if an appropriate [ | + | For sufficiently large values of λ, (say λ>1,000), the [[AP_Statistics_Curriculum_2007_Normal_Prob |Normal(<math>\mu=\lambda, \sigma^2=\lambda</math>)]] distribution is an excellent approximation to the [[AP_Statistics_Curriculum_2007_Distrib_Poisson | Poisson(λ)]] distribution. If λ is greater than about 10, then the normal distribution is a good approximation if an appropriate [http://en.wikipedia.org/wiki/Continuity_correction continuity correction] is performed. Suppose P(''X''≤''x''), where (lower-case) ''x'' is a non-negative integer, is replaced by P(''X'' ≤ ''x'' + 0.5). |
:: <math>F_\mathrm{Poisson}(x;\lambda) \approx F_\mathrm{normal}(x;\mu=\lambda,\sigma^2=\lambda)\,</math> | :: <math>F_\mathrm{Poisson}(x;\lambda) \approx F_\mathrm{normal}(x;\mu=\lambda,\sigma^2=\lambda)\,</math> | ||
| + | If <math>X\sim Poisson(\lambda)</math> and <math>U\sim Normal(<math>\mu=\lambda, \sigma^2=\lambda</math>), then <math>P_X(X<x_o) = P_U(U<x_o+0.5)</math>. | ||
===Examples=== | ===Examples=== | ||
Revision as of 01:58, 3 February 2008
Contents |
General Advance-Placement (AP) Statistics Curriculum - Normal Approximation to Poisson Distribution
Normal Approximation to Poisson Distribution
The Poisson(λ) distribution can be approximated with Normal when λ is large.
For sufficiently large values of λ, (say λ>1,000), the Normal(μ = λ,σ2 = λ) distribution is an excellent approximation to the Poisson(λ) distribution. If λ is greater than about 10, then the normal distribution is a good approximation if an appropriate continuity correction is performed. Suppose P(X≤x), where (lower-case) x is a non-negative integer, is replaced by P(X ≤ x + 0.5).
If 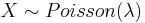 and
and 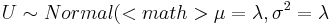 ), then PX(X < xo) = PU(U < xo + 0.5).
), then PX(X < xo) = PU(U < xo + 0.5).
Examples
Suppose cars arrive at a parking lot at a rate of 50 per hour. Let’s assume that the process is a Poisson random variable with λ = 50. Compute the probability that in the next hour the number of cars that arrive at this parking lot will be between 54 and 62. We can compute this as follows:
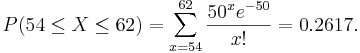 The figure below from SOCR shows this probability.
The figure below from SOCR shows this probability.
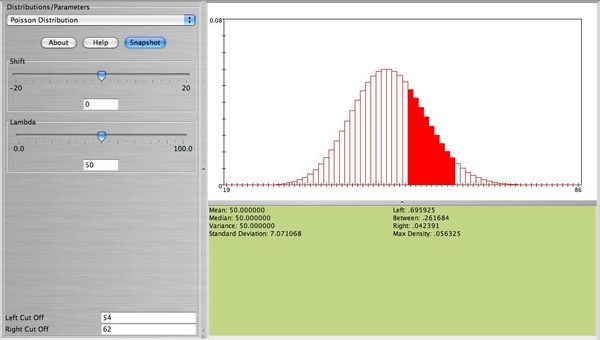
- Note: We observe that this distribution is bell-shaped. We can use the normal distribution to approximate this probability. Using
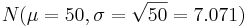 , together with the continuity correction for better approximation we obtain
, together with the continuity correction for better approximation we obtain 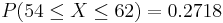 , which is close to the exact that was found earlier. The figure below shows this probability.
, which is close to the exact that was found earlier. The figure below shows this probability.
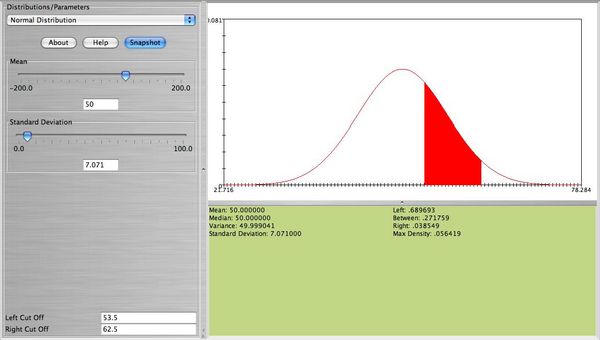
References
- SOCR Home page: http://www.socr.ucla.edu
Translate this page: