AP Statistics Curriculum 2007 MultiVar ANOVA
From Socr
General Advance-Placement (AP) Statistics Curriculum - Multivariate Analysis of Variance
Contents |
Multivariate Analysis of Variance
Multivariate analysis of variance (MANOVA) studies the main and interaction effects of categorical variables on multiple dependent variables. MANOVA uses several categorical independents as predictors, much like ANOVA. However, there is more than one dependent variables. ANOVA tests for differences in means of the dependent for various categories of the independent variables. MANOVA tests the differences in the mean-vector of the multiple dependent variables, for various categories of the independent variables. There are several specific use-cases for MANOVA.
- To compare groups formed by categorical independent variables on group differences in a set of dependent variables.
- To use lack of difference for a set of dependent variables as a criterion for reducing a set of independent variables to a smaller, more easily modeled number of variables.
- To identify the independent variables which differentiate a set of dependent variables the most.
Multiple analysis of covariance (MANCOVA) is similar to MANOVA, but allows adding of interval independents as covariates. These covariates serve as control variables for the independent factors, serving to reduce the error term in the model. Like other control procedures, MANCOVA can be seen as analysis asking what would happen if all cases scored equally on the covariates to enable isolation of the effect of the factors beyond the covariates.
ANOVA/MANOVA parallels
The purpose of the [[EBook#Chapter_VII:_Point_and_Interval_Estimates |T-test is to assess the likelihood that the means for two groups are sampled from the same sampling distribution of means. The purpose of an ANOVA is to test whether the means for two or more groups are taken from the same sampling distribution. The multivariate equivalent of the T-test is Hotelling’s T2. Hotelling’s T2 tests whether the two vectors of means for the two groups are sampled from the same sampling distribution. MANOVA is the multivariate analogue to Hotelling's T2. The purpose of MANOVA is to test whether the vectors of means for the two or more groups are sampled from the same sampling distribution. Just as Hotelling's T2 will provide a measure of the likelihood that two random vectors of means come from the same distribution, MANOVA gives a measure of the overall likelihood of observing two or more random vectors of means out of the same distribution.
MANOVA usage
There are two major situations in which MANOVA is appropriate.
- When there are several correlated dependent variables, and the investigator needs a single, overall
statistical test on this set of variables instead of performing multiple individual tests.
- To explore how independent variables influence some patterning of response on the dependent variables.
Here, one example that uses an analogue of contrast codes on the dependent variables to test hypotheses about how the independent variables differentially predict the dependent variables. MANOVA also has the same problems of multiple post hoc comparisons as ANOVA. An ANOVA gives one overall test of the equality of means for several groups for a single variable. The ANOVA will not tell us which groups differ from each other. MANOVA is one overall test of the equality of mean vectors for several groups. Which specific groups may be different in terms of their mean vectors is a separate question.
Motivational example
This examine will help us motivate and understand the MANOVA design. Suppose a brain mapping researcher is interested in exploring the treatment efficacy of dementia for randomly assigned patients into four conditions (you can find such neuroimaging data here):
- A placebo control group who received physical therapy and a placebo drug;
- A placebo cognitive therapy group who received the placebo medication and a cognitive therapy;
- A medication-treatment control group who received the physical therapy and Vitamin-E medical treatment; and
- An medication-treatment cognitive therapy group who received cognitive therapy and and Vitamin-E medical treatment.
This is a (2 x 2) factorial design with medication (placebo vs. Vitamin-E) as one factor and type of therapy (physical vs. cognitive) as the second factor. Such neuroimaging studies typically collect a number of measures before, during and after the treatment. Suppose there are three outcome measures in this study: Mini-mental State Exam (MMSE) score, Clinical Dementia Rating (CDR) assessment, and non-invasive neuroimaging measures of anatomical atrophy (imaging). High scores on MMSE and low scores on all these measures indicate more depression; low CDR and imaging indicate low measures of dementia (approximate normality). Then the data matrix may look like this:
| Subject | Drug-Treatment | Therapy | MMSE | CDR | Imaging |
|---|---|---|---|---|---|
| Peter | Vitamin-E | Cognitive | 27 | 1.0 | 0.95 |
| Mary | Placebo | Physical | 30 | 0.5 | 0.99 |
| Jennie | Placebo | Cognitive | 23 | 1.3 | 0.94 |
| Jack | Vitamin-E | Physical | 21 | 1.5 | 0.94 |
| ... | ... | ... | ... | ... | ... |
It's better when the study the design is balanced with equal numbers of patients in all four conditions, as this avoid potential problems of sample-size-driven effects (e.g., variance estimates). Recall that a univariate ANOVA (on any single outcome measure) would contain three types of effects -- a main effect for therapy, a mean effect for medication, and an interaction between therapy and medication. Similarly, MANOVA will contain the same three effects.
- Main Effects:
- Therapy: The univariate ANOVA main effect for therapy tells whether the physical vs. cognitive therapy groups have different means, irrespective of their medications. The MANOVA main effect for therapy tells whether the physical vs. cognitive therapy group have different mean vectors irrespective of their medication. The vectors in this case are the (3 x 1) column vectors of means (MMSE, CDR and Imaging).
- Medication: The univariate ANOVA for medication tells whether the placebo group has a different mean from the Vitamin-E group irrespective of the therapy type. The MANOVA main effect for medication tells whether the placebo group has a different mean vector from the VItamin-E group irrespective of therapy.
- Interaction Effects: The univariate ANOVA interaction tells whether the four means for a single variable differ from the value predicted from knowledge of the main effects of therapy and medication. The MANOVA interaction term tells whether the four mean vectors differ from the vector predicted from knowledge of the main effects of therapy and medication.
Variance partitioning
As you can see, MANOVA has the same properties as an ANOVA. The only difference is that an ANOVA deals with a (1 x 1) mean vector for any group (as the response is univatiate). While a MANOVA deals with a (k x 1) vector for any group, k being the number of dependent variables, 3 in our example. The variance-covariance matrix for 1 variable is a (1 x 1) matrix that has only one element, the variance of the variable. What is the variance-covariance matrix for k variables is a (k x k) matrix with the variances on the diagonal and the covariances representing the off diagonal elements. The ANOVA partitions the (1 x 1) covariance matrix into a part due to error and a part due to the researcher-specified hypotheses (the two main effects and the interaction term). That is:
- Vtotal = Vtherapy + Vmedication + Vtherapy * medication + Verror.
Likewise, MANOVA partitions its (k x k) covariance matrix into a part due to research-hypotheses and a part due to error. Thus, in out example, MANOVA will have a (3 x 3) covariance matrix for total variability, a (3 x 3) covariance matrix due to therapy, a (3 x 3) covariance matrix due to medication, a (3 x 3) covariance matrix due to the interaction of therapy with medication, and finally a (3 x 3) covariance matrix for the error. That is:
- Vtotal = Vtherapy + Vmedication + Vtherapy * medication + Verror.
Now, V stands for the appropriate (3 x 3) matrix, as opposed to 1 x 1 value, as in ANOVA. The second equation is the matrix-form of the first one. Here is how we interpret these matrices.
- The Verror matrix will look like this
| MMSE | CDR | Imaging | |
|---|---|---|---|
| MMSE | Verror1 | COV(error1,error2) | COV(error1,error3) |
| CDR | COV(error2,error1) | Verror2 | COV(error2,error3) |
| Imaging | COV(error3,error1) | COV(error3,error2) | Verror3 |
The diagonal elements (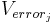 ) are the error variances, for each type of response, and have the same meanings as the error variances in their univariate ANOVA counterparts (an average variability within the four groups). The error variance in MANOVA has the same meaning. That is, if we did a univariate ANOVA for the MMSE alone, the error variance would be the mean squares within groups. Verror1 would be the same means squares within groups -- it would be the same number as in the univariate analysis. The same holds for the mean squares within groups for the CDR and Imaging. The only difference is in the off diagonal elements, which represent the covariances for
the error matrix and must be interpreted as within-group covariances. That is, COV(error1,error2) tells us the extent to which individuals within a group who have high MMSE scores also tend
to have high CDR scores. This covariance matrix can be scaled to correlations to ease the inspection. For example,
) are the error variances, for each type of response, and have the same meanings as the error variances in their univariate ANOVA counterparts (an average variability within the four groups). The error variance in MANOVA has the same meaning. That is, if we did a univariate ANOVA for the MMSE alone, the error variance would be the mean squares within groups. Verror1 would be the same means squares within groups -- it would be the same number as in the univariate analysis. The same holds for the mean squares within groups for the CDR and Imaging. The only difference is in the off diagonal elements, which represent the covariances for
the error matrix and must be interpreted as within-group covariances. That is, COV(error1,error2) tells us the extent to which individuals within a group who have high MMSE scores also tend
to have high CDR scores. This covariance matrix can be scaled to correlations to ease the inspection. For example, 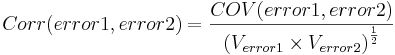 .
.
When analyzing real data, you always have this error covariance matrix and its correlation matrix printed and inspect the correlations. In general, if you could measure enough factors, e.g., covariates, the only remaining variability would be due to random noise and these pair-wise correlations should all go to 0. Thus, inspecting these correlations is often useful because it demonstrates how far we have to go to be able to make predictions (e.g., what is the brain Imaging loss (atrophy), based on different investigator-controlled factors like treatments).
Other MANOVA matrices have their ANOVA analogues. For instance, the variance in MMSE due to therapy calculated from a univariate ANOVA of the MMSE would be the first diagonal element in the Vtherapy matrix. The variance of CDR calculated from a univariate ANOVA is the second diagonal element in Vtherapy. The variance in Imaging due to the interaction between therapy and medication, as calculated from a univariate ANOVA, will be the third diagonal element in Vtherapy * medication. The off diagonal elements are all covariances and should be interpreted as between-group covariances. So, in Vtherapy, COV(1,2) = COV(MMSE, CDR) tells us whether the physical therapy group with the highest mean score on MMSE also has the highest mean score on the CDR. If, cognitive therapy were more efficacious than the physical therapy, then we should expect that all the covariances in Vtherapy be large and positive.
Similarly, COV(2,3) = cov(CDR, Imaging) in the Vtherapy * medication matrix has the following interpretation: if we control for the main effects of therapy and medication, then do groups with high average CDR scores also tend to have high average scores on the brain atrophy as reported by Imaging observations? If there were no main effect for therapy on any of the measures, then all the elements of Vtherapy will be 0. If there were no main effect for medication, then Vmedication will be all 0's. Finally, if there were no interaction, then all of Vtherapy * medication would be 0's. It makes sense to have these matrices manually inspected as they may provide such valuable information about trivial effects or interactions.
Approach
MANOVA calculations closely resemble the ANOVA calculations, except that they are in vector and matrix forms. Assume that instead of a single dependent variance in the one-way ANOVA, there are three dependent variables as in our neuroimaging example above. Under the null hypothesis, it is assumed that scores on the three variables for each of the four groups are sampled from a tri-variate normal distribution mean vector μ = (μ1,μ2,μ3)T and variance-covariance matrix
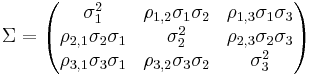 .
.
Where the covariance between variables 1 and 2 is expressed in terms of their correlation (ρ1,2) and individual variances (σ1 and σ2). Under the null hypothesis, the scores for all subjects in groups 1, 2 and 3 are sampled from the same distribution. You can see the complete arithmetic details here and here.
Computational Resources: Internet-based SOCR Tools
Currently under development.
Examples
Currently under development.
Hypotheses testing and inference
There 4 major types of MANOVA tests. The statistical power of these tests differ and follow this rule:
- Pillai’s > Wilk's > Hotelling’s > Roy’s Robustness.
With the Pillai’s test being the most powerful. In general, however, all 4 omnibus tests will agree.
Let the A statistic be the ratio of the sum of squares for an hypothesis and the sum of squares for error. Let H denote the hypothesis sums of squares and cross products matrix, and let E denote the error sums of squares and cross products matrix. The multivariate A statistic is the matrix:
- A = HE − 1
Notice how mean squares (that is, covariance matrices) disappear from MANOVA just as they did for ANOVA. All hypothesis tests may be performed on the matrix A. Note also that because both H and E are symmetric, HE − 1 = E − 1H. This is one special case where the order of matrix multiplication does not matter.
All MANOVA tests are made on A = E − 1H. There are four different multivariate tests that are made on this matrix. Each of the four test statistics has its own associated F ratio. In some cases the four tests give an exact F ratio for testing the null hypothesis and in other cases the F ratio is only approximate. The reason for four different statistics and for approximations is that the MANOVA calculations may be complicated in some cases (i.e., the sampling distribution of the F statistic in some multivariate cases would be difficult to compute exactly.) Suppose there are k dependent variables in the MANOVA, and let λi denote the ith eigenvalue of A = E − 1H.
Wilk’s Λ
This is the most popular test, which expressed as the ratio of determinant-error to determinant-total and represents percent variance not explained in the model. 1 − Λ is an index of variance explained by the model. η2 is a measure of effect size analogous to R2 in regression. You want the Λ value to be small, and this value is transformed into an approximate F for hypothesis-testing. Wilk’s Λ is the pooled ratio of error variances to effect variance plus error variance.
- Wilk's lambda
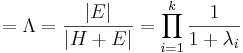 .
.
Pillai’s Trace
Pillai’s criterion is the pooled effect variances.
- Pillai's trace
![= trace[H(H +E)^{-1}] = \sum_{i=1}^k {\lambda_i \over 1 + \lambda_i}](/socr/uploads/math/d/e/1/de10a469a79ca12b7ddc1f8e8aaf144b.png) .
.
Hotelling’s Trace
Hotelling’s trace is the pooled ratio of effect variance to error variance.
- Hotelling-Lawley's
![trace = trace(A) = trace[HE^{-1}] = \sum_{i=1}^k {\lambda_i}](/socr/uploads/math/8/1/b/81b592f059fc1720f739161b8b108cf6.png) .
.
Roy’s Largest (or Characteristic) Root
The Roy's largest root gives an upper bound for the F statistic.
- Roy's largest root = max(λi).
This is the maximum eigenvalue of A = HE − 1. As a root is another name for an eigenvalue, this statistic is also called Roy's largest eigenvalue.
Assumptions
- Observations are independent of one another. The usual MANOVA is not robust when the selection of one observation depends on selection of one or more earlier ones, as in the case of before-after and other repeated measures designs. However, there does exist a variant of MANOVA for repeated measures designs.
- The independent variables are categorical.
- The dependent variables are continuous and interval level.
- Equal group sizes. To the extent that group sizes are very unequal, statistical power diminishes.
- Adequate sample size. Small samples may have lower power. At a minimum, every cell must have more cases than there are dependent variables. With multiple factors and multiple dependents, group sizes fall below minimum levels more easily than in ANOVA/ANCOVA.
- Residuals are randomly distributed, forming a multivariate normal distribution around a mean of zero.
- Homoscedasticity or "homogeneity of variances and covariances": within each group formed by the categorical independents, the error variance of each interval dependent should be similar, as tested by Levene's test. Also, for each of the k groups formed by the independent variables, the covariance between any two dependent variables must be the same. When sample sizes are unequal, tests of group differences (Wilks, Hotelling, Pillai-Bartlett, GCR) are not robust when this assumption is violated.
- Sphericity. In a repeated measures design, the univariate ANOVA tables will not be interpreted properly unless the variance/covariance matrix of the dependent variables is circular in form. A spherical model implies that the assumptions of multiple univariate ANOVA is met, that the repeated contrasts are uncorrelated. When there is a violation of this assumption in a repeated measures design, the researcher should use MANOVA rather than multiple univariate ANOVA tests.
- Multivariate normal distribution. For purposes of significance testing, response (dependent) variables are assumed to have multivariate normal distributions. In practice, it is common to assume multivariate normality if each variable considered separately follows a normal distribution. MANOVA is robust in the face of most violations of this assumption if sample size is not small (e.g., < 15) and there are no outliers.
- No outliers. MANCOVA is highly sensitive to outliers in the covariates, its robustness against other types of non-normality notwithstanding.
- Covariates are linearly related or in a known relationship to the dependents. The form of the relationship between the covariate and the dependent must be known and most computer programs assume this relationship is linear, adjusting the dependent mean based on linear regression. Scatterplots of the covariate and the dependent for each of the k groups formed by the independents is one way to assess violations of this assumption. Covariates may be transformed (e.g., log transform) to establish a linear relationship.
References
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:
