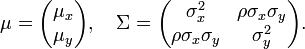AP Statistics Curriculum 2007 MultivariateNormal
From Socr
(Created page with '== EBook - Multivariate Normal Distribution== The multivariate normal distribution, or multivariate Gaussian distribution, is a generalization…') |
m (→Definition: typos) |
||
| Line 4: | Line 4: | ||
=== Definition=== | === Definition=== | ||
| - | In k-dimensions, a random vector <math>X = ( | + | In k-dimensions, a random vector <math>X = (X_1, \cdots, X_k)</math> is multivariate normally distributed if it satisfies any one of the following ''equivalent'' conditions <ref>Gut, Allan: An Intermediate Course in Probability, Springer 2009, chapter 5, http://books.google.com/books?id=ufxMwdtrmOAC, ISBN 9781441901613</ref>: |
| - | * Every linear combination of its components ''Y'' = ''a''<sub>1</sub>''X''<sub>1</sub> + … + ''a<sub>k</sub>X<sub>k</sub>'' is [[AP_Statistics_Curriculum_2007_Normal_Prob|normally distributed]]. In other words, for any constant vector | + | * Every linear combination of its components ''Y'' = ''a''<sub>1</sub>''X''<sub>1</sub> + … + ''a<sub>k</sub>X<sub>k</sub>'' is [[AP_Statistics_Curriculum_2007_Normal_Prob|normally distributed]]. In other words, for any constant vector <math>a\in R^k</math>, the linear combination (which is univariate random variable) <math>Y = a^TX = \sum_{i=1}^{k}{a_iX_i}</math> has a univariate normal distribution. |
| - | * There exists a random ''ℓ''-vector ''Z'', whose components are independent normal random variables, a ''k''-vector ''μ'', and a ''k×ℓ'' | + | * There exists a random ''ℓ''-vector ''Z'', whose components are independent normal random variables, a ''k''-vector ''μ'', and a ''k×ℓ'' matrix ''A'', such that <math>X = AZ + \mu</math>. Here ''ℓ'' is the ''rank'' of the variance-covariance matrix. |
* There is a ''k''-vector ''μ'' and a symmetric, nonnegative-definite ''k×k'' matrix Σ, such that the characteristic function of ''X'' is | * There is a ''k''-vector ''μ'' and a symmetric, nonnegative-definite ''k×k'' matrix Σ, such that the characteristic function of ''X'' is | ||
: <math> | : <math> | ||
| - | \varphi_X(u) = \exp\Big( iu | + | \varphi_X(u) = \exp\Big( iu^T\mu - \tfrac{1}{2} u^T\Sigma u \Big). |
</math> | </math> | ||
Revision as of 05:17, 14 December 2010
Contents |
EBook - Multivariate Normal Distribution
The multivariate normal distribution, or multivariate Gaussian distribution, is a generalization of the univariate (one-dimensional) normal distribution to higher dimensions. A random vector is said to be multivariate normally distributed if every linear combination of its components has a univariate normal distribution. The multivariate normal distribution may be used to study different associations (e.g., correlations) between real-valued random variables.
Definition
In k-dimensions, a random vector 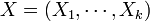 is multivariate normally distributed if it satisfies any one of the following equivalent conditions <ref>Gut, Allan: An Intermediate Course in Probability, Springer 2009, chapter 5, http://books.google.com/books?id=ufxMwdtrmOAC, ISBN 9781441901613</ref>:
is multivariate normally distributed if it satisfies any one of the following equivalent conditions <ref>Gut, Allan: An Intermediate Course in Probability, Springer 2009, chapter 5, http://books.google.com/books?id=ufxMwdtrmOAC, ISBN 9781441901613</ref>:
- Every linear combination of its components Y = a1X1 + … + akXk is normally distributed. In other words, for any constant vector
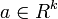 , the linear combination (which is univariate random variable)
, the linear combination (which is univariate random variable) 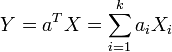 has a univariate normal distribution.
has a univariate normal distribution.
- There exists a random ℓ-vector Z, whose components are independent normal random variables, a k-vector μ, and a k×ℓ matrix A, such that X = AZ + μ. Here ℓ is the rank of the variance-covariance matrix.
- There is a k-vector μ and a symmetric, nonnegative-definite k×k matrix Σ, such that the characteristic function of X is
- When the support of X is the entire space Rk, there exists a k-vector μ and a symmetric positive-definite k×k variance-covariance matrix Σ, such that the probability density function of X can be expressed as
where |Σ| is the determinant of Σ, and where (2π)k/2|Σ|1/2 = |2πΣ|1/2. This formulation reduces to the density of the univariate normal distribution if Σ is a scalar (i.e., a 1×1 matrix).
If the variance-covariance matrix is singular, the corresponding distribution has no density. An example of this case is the distribution of the vector of residual-errors in the ordinary least squares regression. Note also that the Xi are in general not independent; they can be seen as the result of applying the matrix A to a collection of independent Gaussian variables Z.
Bivariate (2D) case
In 2-dimensions, the nonsingular bi-variate Normal distribution with (Template:Nowrap), the probability density function of a (bivariate) vector Template:Nowrap is
where ρ is the correlation between X and Y. In this case,
In the bivariate case, the first equivalent condition for multivariate normality is less restrictive: it is sufficient to verify that countably many distinct linear combinations of X and Y are normal in order to conclude that the vector Template:Nowrap is bivariate normal.
Properties
Normally distributed and independent
If X and Y are normally distributed and independent, this implies they are "jointly normally distributed", hence, the pair (X, Y) must have bivariate normal distribution. However, a pair of jointly normally distributed variables need not be independent - they could be correlated.
Two normally distributed random variables need not be jointly bivariate normal
The fact that two random variables X and Y both have a normal distribution does not imply that the pair (X, Y) has a joint normal distribution. A simple example is one in which X has a normal distribution with expected value 0 and variance 1, and Y = X if |X| > c and Y = −X if |X| < c, where c is about 1.54.
Problems
References
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:
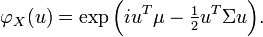
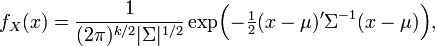
![f(x,y) =
\frac{1}{2 \pi \sigma_x \sigma_y \sqrt{1-\rho^2}}
\exp\left(
-\frac{1}{2(1-\rho^2)}\left[
\frac{(x-\mu_x)^2}{\sigma_x^2} +
\frac{(y-\mu_y)^2}{\sigma_y^2} -
\frac{2\rho(x-\mu_x)(y-\mu_y)}{\sigma_x \sigma_y}
\right]
\right),](/socr/uploads/math/b/1/0/b10ecc56f758b2f94a953e7e1bd2f1c2.png)