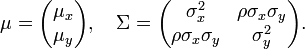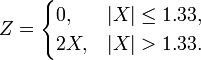AP Statistics Curriculum 2007 MultivariateNormal
From Socr
(Created page with '== EBook - Multivariate Normal Distribution== The multivariate normal distribution, or multivariate Gaussian distribution, is a generalization…') |
(→Bivariate (2D) case) |
||
| (12 intermediate revisions not shown) | |||
| Line 4: | Line 4: | ||
=== Definition=== | === Definition=== | ||
| - | In k-dimensions, a random vector <math>X = ( | + | In k-dimensions, a random vector <math>X = (X_1, \cdots, X_k)</math> is multivariate normally distributed if it satisfies any one of the following ''equivalent'' conditions (Gut, 2009): |
| - | * Every linear combination of its components ''Y'' = ''a''<sub>1</sub>''X''<sub>1</sub> + … + ''a<sub>k</sub>X<sub>k</sub>'' is [[AP_Statistics_Curriculum_2007_Normal_Prob|normally distributed]]. In other words, for any constant vector | + | * Every linear combination of its components ''Y'' = ''a''<sub>1</sub>''X''<sub>1</sub> + … + ''a<sub>k</sub>X<sub>k</sub>'' is [[AP_Statistics_Curriculum_2007_Normal_Prob|normally distributed]]. In other words, for any constant vector <math>a\in R^k</math>, the linear combination (which is univariate random variable) <math>Y = a^TX = \sum_{i=1}^{k}{a_iX_i}</math> has a univariate normal distribution. |
| - | * There exists a random ''ℓ''-vector ''Z'', whose components are independent normal random variables, a ''k''-vector ''μ'', and a ''k×ℓ'' | + | * There exists a random ''ℓ''-vector ''Z'', whose components are independent normal random variables, a ''k''-vector ''μ'', and a ''k×ℓ'' matrix ''A'', such that <math>X = AZ + \mu</math>. Here ''ℓ'' is the ''rank'' of the variance-covariance matrix. |
* There is a ''k''-vector ''μ'' and a symmetric, nonnegative-definite ''k×k'' matrix Σ, such that the characteristic function of ''X'' is | * There is a ''k''-vector ''μ'' and a symmetric, nonnegative-definite ''k×k'' matrix Σ, such that the characteristic function of ''X'' is | ||
: <math> | : <math> | ||
| - | \varphi_X(u) = \exp\Big( iu | + | \varphi_X(u) = \exp\Big( iu^T\mu - \tfrac{1}{2} u^T\Sigma u \Big). |
</math> | </math> | ||
| Line 18: | Line 18: | ||
: <math> | : <math> | ||
f_X(x) = \frac{1}{ (2\pi)^{k/2}|\Sigma|^{1/2} } | f_X(x) = \frac{1}{ (2\pi)^{k/2}|\Sigma|^{1/2} } | ||
| - | \exp\!\Big( {-\tfrac{1}{2}}(x-\mu)'\Sigma^{-1}(x-\mu) \Big) | + | \exp\!\Big( {-\tfrac{1}{2}}(x-\mu)'\Sigma^{-1}(x-\mu) \Big) |
| - | </math> | + | </math>, where |Σ| is the determinant of Σ, and where (2π)<sup>''k''/2</sup>|Σ|<sup>1/2</sup> = |2πΣ|<sup>1/2</sup>. This formulation reduces to the density of the univariate normal distribution if Σ is a scalar (i.e., a 1×1 matrix). |
| - | where |Σ| is the determinant of Σ, and where (2π)<sup>''k''/2</sup>|Σ|<sup>1/2</sup> = |2πΣ|<sup>1/2</sup>. This formulation reduces to the density of the univariate normal distribution if Σ is a scalar (i.e., a 1×1 matrix). | + | |
If the variance-covariance matrix is singular, the corresponding distribution has no density. An example of this case is the distribution of the vector of residual-errors in the ordinary least squares regression. Note also that the ''X''<sub>''i''</sub> are in general ''not'' independent; they can be seen as the result of applying the matrix ''A'' to a collection of independent Gaussian variables ''Z''. | If the variance-covariance matrix is singular, the corresponding distribution has no density. An example of this case is the distribution of the vector of residual-errors in the ordinary least squares regression. Note also that the ''X''<sub>''i''</sub> are in general ''not'' independent; they can be seen as the result of applying the matrix ''A'' to a collection of independent Gaussian variables ''Z''. | ||
| - | |||
| - | |||
===Bivariate (2D) case=== | ===Bivariate (2D) case=== | ||
| - | In 2-dimensions, the nonsingular bi-variate Normal distribution with ( | + | : See the SOCR Bivariate Normal Distribution [[SOCR_BivariateNormal_JS_Activity| Activity]] and corresponding [http://socr.ucla.edu/htmls/HTML5/BivariateNormal/ Webapp]. |
| + | |||
| + | In 2-dimensions, the nonsingular bi-variate Normal distribution with (<math>k=rank(\Sigma) = 2</math>), the probability density function of a (bivariate) vector (X,Y) is | ||
: <math> | : <math> | ||
f(x,y) = | f(x,y) = | ||
| Line 46: | Line 45: | ||
</math> | </math> | ||
| - | In the bivariate case, the first equivalent condition for multivariate normality is less restrictive: it is sufficient to verify that countably many distinct linear combinations of X and Y are normal in order to conclude that the vector | + | In the bivariate case, the first equivalent condition for multivariate normality is less restrictive: it is sufficient to verify that countably many distinct linear combinations of X and Y are normal in order to conclude that the vector <math> [ X, Y ] ^T</math> is bivariate normal. |
===Properties=== | ===Properties=== | ||
| Line 53: | Line 52: | ||
====Two normally distributed random variables need not be jointly bivariate normal==== | ====Two normally distributed random variables need not be jointly bivariate normal==== | ||
| - | The fact that two random variables ''X'' and ''Y'' both have a normal distribution does not imply that the pair (''X'', ''Y'') has a joint normal distribution. A simple example is | + | The fact that two random variables ''X'' and ''Y'' both have a normal distribution does not imply that the pair (''X'', ''Y'') has a joint normal distribution. A simple example is provided below: |
| + | : Let X ~ N(0,1). | ||
| + | : Let <math>Y = \begin{cases} X,& |X| > 1.33,\\ | ||
| + | -X,& |X| \leq 1.33.\end{cases}</math> | ||
| + | Then, both X and Y are individually Normally distributed; however, the pair (X,Y) is '''not''' jointly bivariate Normal distributed (of course, the constant c=1.33 is not special, any other non-trivial constant also works). | ||
| + | |||
| + | Furthermore, as X and Y are not independent, the sum Z = X+Y is not guaranteed to be a (univariate) Normal variable. In this case, it's clear that Z is not Normal: | ||
| + | : <math>Z = \begin{cases} 0,& |X| \leq 1.33,\\ | ||
| + | 2X,& |X| > 1.33.\end{cases}</math> | ||
| + | |||
| + | ===Applications=== | ||
| + | [[SOCR_EduMaterials_Activities_2D_PointSegmentation_EM_Mixture| This SOCR activity demonstrates the use of 2D Gaussian distribution, expectation maximization and mixture modeling for classification of points (objects) in 2D]]. | ||
===[[EBook_Problems_MultivariateNormal|Problems]]=== | ===[[EBook_Problems_MultivariateNormal|Problems]]=== | ||
| Line 61: | Line 71: | ||
===References=== | ===References=== | ||
| - | + | * Gut, A. (2009): [http://books.google.com/books?id=ufxMwdtrmOAC An Intermediate Course in Probability, Springer 2009, chapter 5, ISBN 9781441901613]. | |
<hr> | <hr> | ||
Current revision as of 00:02, 22 July 2012
Contents |
EBook - Multivariate Normal Distribution
The multivariate normal distribution, or multivariate Gaussian distribution, is a generalization of the univariate (one-dimensional) normal distribution to higher dimensions. A random vector is said to be multivariate normally distributed if every linear combination of its components has a univariate normal distribution. The multivariate normal distribution may be used to study different associations (e.g., correlations) between real-valued random variables.
Definition
In k-dimensions, a random vector 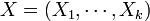 is multivariate normally distributed if it satisfies any one of the following equivalent conditions (Gut, 2009):
is multivariate normally distributed if it satisfies any one of the following equivalent conditions (Gut, 2009):
- Every linear combination of its components Y = a1X1 + … + akXk is normally distributed. In other words, for any constant vector
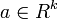 , the linear combination (which is univariate random variable)
, the linear combination (which is univariate random variable) 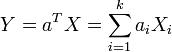 has a univariate normal distribution.
has a univariate normal distribution.
- There exists a random ℓ-vector Z, whose components are independent normal random variables, a k-vector μ, and a k×ℓ matrix A, such that X = AZ + μ. Here ℓ is the rank of the variance-covariance matrix.
- There is a k-vector μ and a symmetric, nonnegative-definite k×k matrix Σ, such that the characteristic function of X is
- When the support of X is the entire space Rk, there exists a k-vector μ and a symmetric positive-definite k×k variance-covariance matrix Σ, such that the probability density function of X can be expressed as
-
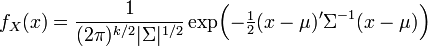 , where |Σ| is the determinant of Σ, and where (2π)k/2|Σ|1/2 = |2πΣ|1/2. This formulation reduces to the density of the univariate normal distribution if Σ is a scalar (i.e., a 1×1 matrix).
, where |Σ| is the determinant of Σ, and where (2π)k/2|Σ|1/2 = |2πΣ|1/2. This formulation reduces to the density of the univariate normal distribution if Σ is a scalar (i.e., a 1×1 matrix).
If the variance-covariance matrix is singular, the corresponding distribution has no density. An example of this case is the distribution of the vector of residual-errors in the ordinary least squares regression. Note also that the Xi are in general not independent; they can be seen as the result of applying the matrix A to a collection of independent Gaussian variables Z.
Bivariate (2D) case
In 2-dimensions, the nonsingular bi-variate Normal distribution with (k = rank(Σ) = 2), the probability density function of a (bivariate) vector (X,Y) is
where ρ is the correlation between X and Y. In this case,
In the bivariate case, the first equivalent condition for multivariate normality is less restrictive: it is sufficient to verify that countably many distinct linear combinations of X and Y are normal in order to conclude that the vector [X,Y]T is bivariate normal.
Properties
Normally distributed and independent
If X and Y are normally distributed and independent, this implies they are "jointly normally distributed", hence, the pair (X, Y) must have bivariate normal distribution. However, a pair of jointly normally distributed variables need not be independent - they could be correlated.
Two normally distributed random variables need not be jointly bivariate normal
The fact that two random variables X and Y both have a normal distribution does not imply that the pair (X, Y) has a joint normal distribution. A simple example is provided below:
- Let X ~ N(0,1).
- Let
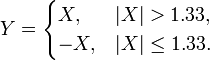
Then, both X and Y are individually Normally distributed; however, the pair (X,Y) is not jointly bivariate Normal distributed (of course, the constant c=1.33 is not special, any other non-trivial constant also works).
Furthermore, as X and Y are not independent, the sum Z = X+Y is not guaranteed to be a (univariate) Normal variable. In this case, it's clear that Z is not Normal:
Applications
Problems
References
- Gut, A. (2009): An Intermediate Course in Probability, Springer 2009, chapter 5, ISBN 9781441901613.
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:
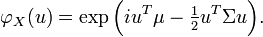
![f(x,y) =
\frac{1}{2 \pi \sigma_x \sigma_y \sqrt{1-\rho^2}}
\exp\left(
-\frac{1}{2(1-\rho^2)}\left[
\frac{(x-\mu_x)^2}{\sigma_x^2} +
\frac{(y-\mu_y)^2}{\sigma_y^2} -
\frac{2\rho(x-\mu_x)(y-\mu_y)}{\sigma_x \sigma_y}
\right]
\right),](/socr/uploads/math/b/1/0/b10ecc56f758b2f94a953e7e1bd2f1c2.png)