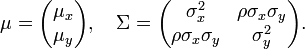AP Statistics Curriculum 2007 MultivariateNormal
From Socr
m (→Bivariate (2D) case: typos) |
m (→Definition) |
||
| Line 18: | Line 18: | ||
: <math> | : <math> | ||
f_X(x) = \frac{1}{ (2\pi)^{k/2}|\Sigma|^{1/2} } | f_X(x) = \frac{1}{ (2\pi)^{k/2}|\Sigma|^{1/2} } | ||
| - | \exp\!\Big( {-\tfrac{1}{2}}(x-\mu)'\Sigma^{-1}(x-\mu) \Big) | + | \exp\!\Big( {-\tfrac{1}{2}}(x-\mu)'\Sigma^{-1}(x-\mu) \Big) |
| - | </math> | + | </math>, where |Σ| is the determinant of Σ, and where (2π)<sup>''k''/2</sup>|Σ|<sup>1/2</sup> = |2πΣ|<sup>1/2</sup>. This formulation reduces to the density of the univariate normal distribution if Σ is a scalar (i.e., a 1×1 matrix). |
| - | where |Σ| is the determinant of Σ, and where (2π)<sup>''k''/2</sup>|Σ|<sup>1/2</sup> = |2πΣ|<sup>1/2</sup>. This formulation reduces to the density of the univariate normal distribution if Σ is a scalar (i.e., a 1×1 matrix). | + | |
If the variance-covariance matrix is singular, the corresponding distribution has no density. An example of this case is the distribution of the vector of residual-errors in the ordinary least squares regression. Note also that the ''X''<sub>''i''</sub> are in general ''not'' independent; they can be seen as the result of applying the matrix ''A'' to a collection of independent Gaussian variables ''Z''. | If the variance-covariance matrix is singular, the corresponding distribution has no density. An example of this case is the distribution of the vector of residual-errors in the ordinary least squares regression. Note also that the ''X''<sub>''i''</sub> are in general ''not'' independent; they can be seen as the result of applying the matrix ''A'' to a collection of independent Gaussian variables ''Z''. | ||
| - | |||
| - | |||
===Bivariate (2D) case=== | ===Bivariate (2D) case=== | ||
Revision as of 05:33, 14 December 2010
Contents |
EBook - Multivariate Normal Distribution
The multivariate normal distribution, or multivariate Gaussian distribution, is a generalization of the univariate (one-dimensional) normal distribution to higher dimensions. A random vector is said to be multivariate normally distributed if every linear combination of its components has a univariate normal distribution. The multivariate normal distribution may be used to study different associations (e.g., correlations) between real-valued random variables.
Definition
In k-dimensions, a random vector 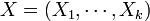 is multivariate normally distributed if it satisfies any one of the following equivalent conditions (Gut, 2009):
is multivariate normally distributed if it satisfies any one of the following equivalent conditions (Gut, 2009):
- Every linear combination of its components Y = a1X1 + … + akXk is normally distributed. In other words, for any constant vector
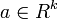 , the linear combination (which is univariate random variable)
, the linear combination (which is univariate random variable) 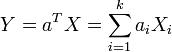 has a univariate normal distribution.
has a univariate normal distribution.
- There exists a random ℓ-vector Z, whose components are independent normal random variables, a k-vector μ, and a k×ℓ matrix A, such that X = AZ + μ. Here ℓ is the rank of the variance-covariance matrix.
- There is a k-vector μ and a symmetric, nonnegative-definite k×k matrix Σ, such that the characteristic function of X is
- When the support of X is the entire space Rk, there exists a k-vector μ and a symmetric positive-definite k×k variance-covariance matrix Σ, such that the probability density function of X can be expressed as
-
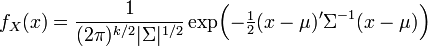 , where |Σ| is the determinant of Σ, and where (2π)k/2|Σ|1/2 = |2πΣ|1/2. This formulation reduces to the density of the univariate normal distribution if Σ is a scalar (i.e., a 1×1 matrix).
, where |Σ| is the determinant of Σ, and where (2π)k/2|Σ|1/2 = |2πΣ|1/2. This formulation reduces to the density of the univariate normal distribution if Σ is a scalar (i.e., a 1×1 matrix).
If the variance-covariance matrix is singular, the corresponding distribution has no density. An example of this case is the distribution of the vector of residual-errors in the ordinary least squares regression. Note also that the Xi are in general not independent; they can be seen as the result of applying the matrix A to a collection of independent Gaussian variables Z.
Bivariate (2D) case
In 2-dimensions, the nonsingular bi-variate Normal distribution with (k = rank(Σ) = 2), the probability density function of a (bivariate) vector (X,Y) is
where ρ is the correlation between X and Y. In this case,
In the bivariate case, the first equivalent condition for multivariate normality is less restrictive: it is sufficient to verify that countably many distinct linear combinations of X and Y are normal in order to conclude that the vector [X,Y]T is bivariate normal.
Properties
Normally distributed and independent
If X and Y are normally distributed and independent, this implies they are "jointly normally distributed", hence, the pair (X, Y) must have bivariate normal distribution. However, a pair of jointly normally distributed variables need not be independent - they could be correlated.
Two normally distributed random variables need not be jointly bivariate normal
The fact that two random variables X and Y both have a normal distribution does not imply that the pair (X, Y) has a joint normal distribution. A simple example is one in which X has a normal distribution with expected value 0 and variance 1, and Y = X if |X| > c and Y = −X if |X| < c, where c is about 1.54.
Problems
References
- Gut, A. (2009): An Intermediate Course in Probability, Springer 2009, chapter 5, ISBN 9781441901613.
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:
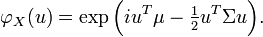
![f(x,y) =
\frac{1}{2 \pi \sigma_x \sigma_y \sqrt{1-\rho^2}}
\exp\left(
-\frac{1}{2(1-\rho^2)}\left[
\frac{(x-\mu_x)^2}{\sigma_x^2} +
\frac{(y-\mu_y)^2}{\sigma_y^2} -
\frac{2\rho(x-\mu_x)(y-\mu_y)}{\sigma_x \sigma_y}
\right]
\right),](/socr/uploads/math/b/1/0/b10ecc56f758b2f94a953e7e1bd2f1c2.png)