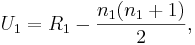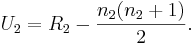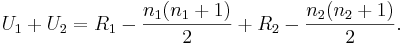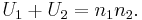AP Statistics Curriculum 2007 NonParam 2MedianIndep
From Socr
(→WMW Test vs. Independent T-Test) |
|||
| (12 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
==[[AP_Statistics_Curriculum_2007 | General Advance-Placement (AP) Statistics Curriculum]] - Difference of Medians of Two Independent Samples== | ==[[AP_Statistics_Curriculum_2007 | General Advance-Placement (AP) Statistics Curriculum]] - Difference of Medians of Two Independent Samples== | ||
| - | As we | + | As we discussed in the [[AP_Statistics_Curriculum_2007_NonParam_2MedianPair | paired case]], non-parametric statistical methods provide alternatives to the (standard) [[EBook#Chapter_VIII:_Hypothesis_Testing | parametric tests that we saw earlier]], and they are applicable when the distribution of the data is unknown. |
| - | ==Motivational Example== | + | ===Motivational Example=== |
| - | Nine observations of surface soil [http://en.wikipedia.org/wiki/PH pH] were made at two different (independent) locations. Does the data suggest that the true mean soil [http://en.wikipedia.org/wiki/PH pH] values | + | Nine observations of surface soil [http://en.wikipedia.org/wiki/PH pH] were made at two different (independent) locations. Does the data suggest that the true mean soil [http://en.wikipedia.org/wiki/PH pH] values differs for the two locations? Note that there is no pairing in this design, even though this is a balanced design with 9 observations in each (independent) group. Test using <math>\alpha = 0.05</math>, and be sure to check any necessary assumptions for the validity of your test. |
<center> | <center> | ||
| Line 31: | Line 31: | ||
</center> | </center> | ||
| - | We see the clear analogy of this study design to the [[AP_Statistics_Curriculum_2007_Infer_2Means_Indep |independent 2-sample designs]] we saw before. However, if we were to plot these data we can see that their distributions may be different or not even symmetric, unimodal and bell-shaped (i.e., not Normal). Therefore, we | + | We see the clear analogy of this study design to the [[AP_Statistics_Curriculum_2007_Infer_2Means_Indep |independent 2-sample designs]] we saw before. However, if we were to plot these data we can see that their distributions may be different or not even symmetric, unimodal and bell-shaped (i.e., not Normal). Therefore, we cannot use the [[AP_Statistics_Curriculum_2007_Infer_2Means_Indep |Independent T-Test]] to test a Null-hypothesis that the centers of the two distributions (that the 2 samples came from) are identical, using this parametric test. |
<center>[[Image:SOCR_EBook_Dinov_NonParam_Wilcoxon_022408_Fig1.jpg|600px]] | <center>[[Image:SOCR_EBook_Dinov_NonParam_Wilcoxon_022408_Fig1.jpg|600px]] | ||
[[Image:SOCR_EBook_Dinov_NonParam_Wilcoxon_022408_Fig2.jpg|600px]]</center> | [[Image:SOCR_EBook_Dinov_NonParam_Wilcoxon_022408_Fig2.jpg|600px]]</center> | ||
| - | The first | + | The first figure shows the index plot of the pH levels for both samples. The second figure shows the sample histograms of these samples, which are clearly not Normal-like. Therefore, the [[AP_Statistics_Curriculum_2007_Infer_2Means_Indep |Independent T-Test]] would not be appropriate to analyze these data. |
| - | Intuitively, we may consider these group differences significantly large, | + | Intuitively, we may consider these group differences significantly large, especially if we look at the [[SOCR_EduMaterials_Activities_BoxPlot | Box-and-Whisker Plots]], but this is a qualitative inference that demands a more quantitative statistical analysis that can back up our intuition. |
<center>[[Image:SOCR_EBook_Dinov_NonParam_Wilcoxon_022408_Fig3.jpg|600px]]</center> | <center>[[Image:SOCR_EBook_Dinov_NonParam_Wilcoxon_022408_Fig3.jpg|600px]]</center> | ||
==The Wilcoxon-Mann-Whitney Test== | ==The Wilcoxon-Mann-Whitney Test== | ||
| - | The | + | The Wilcoxon-Mann-Whitney (WMW) Test (also known as Mann-Whitney U Test, Mann-Whitney-Wilcoxon Test, or Wilcoxon Rank-Sum Test) is a non-parametric test for assessing whether two samples come from the same distribution. The null hypothesis is that the two samples are drawn from a single population, and therefore that their probability distributions are equal. It requires that the two samples are independent, and that the observations are [[AP_Statistics_Curriculum_2007#Types_of_Data |ordinal]] or continuous measurements. |
| - | + | ||
===Calculations=== | ===Calculations=== | ||
| - | + | The ''U'' statistic for the WMW test may be approximated for sample sizes above about 20 using the [[AP_Statistics_Curriculum_2007#Chapter_V:_Normal_Probability_Distribution |Normal Distribution]]. | |
| - | : | + | The ''U'' test is provided as part of [http://socr.ucla.edu/htmls/SOCR_Analyses.html SOCR Analyses] - [[SOCR_EduMaterials_AnalysisActivities_Wilcoxon |see this activity]]. |
| - | + | ||
| - | + | For small samples, we can directly compute the WMW test-statistic as follows. | |
| - | + | ||
| - | + | # Choose the sample for which the ranks seem to be smaller. Call this ''Sample 1'', and call the other sample ''Sample 2.'' | |
| - | + | # Taking each observation in ''Sample 2'', count the number of observations in ''Sample 1'' that are smaller than it (count 0.5 for any that are equal to it). | |
| - | + | # The total of these counts is ''U''. | |
| - | + | For larger samples, a formula can be used: | |
| - | + | # Arrange all the observations into a single ranked series. That is, rank all the observations without regard to which sample they come from. | |
| - | + | # Add up the ranks in ''Sample 1''. The sum of ranks in ''Sample 2'' follows by calculation, since the sum of all the ranks equals ''N'' (''N'' + 1)/2, where ''N'' is the total number of observations. | |
| - | + | ||
| - | + | # "U" is then given by: | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | :<math>U_1=R_1 - {n_1(n_1+1) \over 2} \,\!,</math> | |
| - | < | + | where ''n''<sub>1</sub> is the two sample size for ''Sample 1'', and ''R''<sub>1</sub> is the sum of the ranks in ''Sample 1''. |
| - | + | :Note that there is no specification as to which sample is considered ''Sample 1''. An equally valid formula for ''U'' is | |
| + | ::<math>U_2=R_2 - {n_2(n_2+1) \over 2}. \,\!</math> | ||
| - | < | + | :The sum of the two values is then given by |
| + | ::<math>U_1 + U_2 = R_1 - {n_1(n_1+1) \over 2} + R_2 - {n_2(n_2+1) \over 2}. \,\!</math> | ||
| - | + | : Knowing that ''R''<sub>1</sub> + ''R''<sub>2</sub> = ''N''(''N'' + 1)/2 and ''N'' = ''n''<sub>1</sub> + ''n''<sub>2</sub> , and doing some algebra, we find that the sum is | |
| + | ::<math>U_1 + U_2 = n_1 n_2. \,\!</math> | ||
| - | + | The maximum value of ''U'' is the product of the sample sizes for the two samples. In such a case, the "other" ''U'' would be 0. | |
| - | + | ===The Wilcoxon-Mann-Whitney Test Using SOCR Analyses=== | |
| + | It is much quicker to use [http://socr.ucla.edu/htmls/SOCR_Analyses.html SOCR Analyses] to compute the statistical significance of the sign test. This [[SOCR_EduMaterials_AnalysisActivities_Wilcoxon | SOCR Wilcoxon-Mann-Whitney Test Activity]] may also be helpful in understanding how to use this test in SOCR. We have the following results for the pH data above: | ||
| - | + | <center>[[Image:SOCR_EBook_Dinov_NonParam_Wilcoxon_022408_Fig4.jpg|600px]]</center> | |
| - | [[ | + | |
| - | < | + | Clearly the p-value < 0.05, and therefore our data provides sufficient evidence to reject the null hypothesis. So we assumes that there were significant pH differences between the two soil lots tested in this experiment. |
| - | + | : One-Sided P-Value for Sample2 < Sample1: 0.00040 | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | : Two-Sided P-Value for Sample1 not equal to Sample2: 0.00079 | |
| - | + | ==WMW Test vs. [[AP_Statistics_Curriculum_2007_Infer_2Means_Indep |Independent T-Test]]== | |
| - | + | Both types of tests answer the same question, but treat data differently. | |
| - | : | + | *The WMW test uses rank ordering |
| + | : Positive: Doesn’t depend on normality or population parameters | ||
| + | : Negative: Distribution free lacks power because it doesn't use all the info in the data | ||
| - | + | * The T-test uses the raw measurements | |
| - | + | : Positive: Incorporates all of the data into calculations | |
| + | : Negative: Must meet normality assumption | ||
| + | |||
| + | * Neither test is uniformly superior. If the data are normally distributed we use the T-test. If the data are not normal use the WMW test. | ||
| + | |||
| + | ==Practice Examples== | ||
| + | |||
| + | ===Urinary Fluoride Concentration in Cattle=== | ||
| + | The urinary fluoride concentration (ppm) was measured both for a sample of livestock grazing in an area previously exposed to fluoride pollution and also for a similar sample of livestock grazing in an unpolluted area. | ||
<center> | <center> | ||
| - | {| class="wikitable" style="text-align:center; width: | + | {| class="wikitable" style="text-align:center; width:35%" border="1" |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
|- | |- | ||
| - | | | + | | '''Polluted''' || '''Unpolluted''' |
|- | |- | ||
| - | | | + | | 21.3 || 10.1 |
|- | |- | ||
| - | | | + | | 18.7 || 18.3 |
|- | |- | ||
| - | | | + | | 21.4 || 17.2 |
|- | |- | ||
| - | | | + | | 17.1 || 18.4 |
|- | |- | ||
| - | | | + | | 11.1 || 20.0 |
|- | |- | ||
| - | | 9 || | + | | 20.9 || |
|- | |- | ||
| - | | | + | | 19.7 || |
|} | |} | ||
</center> | </center> | ||
==References== | ==References== | ||
| - | |||
<hr> | <hr> | ||
Current revision as of 20:59, 28 June 2010
Contents |
General Advance-Placement (AP) Statistics Curriculum - Difference of Medians of Two Independent Samples
As we discussed in the paired case, non-parametric statistical methods provide alternatives to the (standard) parametric tests that we saw earlier, and they are applicable when the distribution of the data is unknown.
Motivational Example
Nine observations of surface soil pH were made at two different (independent) locations. Does the data suggest that the true mean soil pH values differs for the two locations? Note that there is no pairing in this design, even though this is a balanced design with 9 observations in each (independent) group. Test using α = 0.05, and be sure to check any necessary assumptions for the validity of your test.
| Location 1 | Location 2 |
| 8.10 | 7.85 |
| 7.89 | 7.30 |
| 8.00 | 7.73 |
| 7.85 | 7.27 |
| 8.01 | 7.58 |
| 7.82 | 7.27 |
| 7.99 | 7.50 |
| 7.80 | 7.23 |
| 7.93 | 7.41 |
We see the clear analogy of this study design to the independent 2-sample designs we saw before. However, if we were to plot these data we can see that their distributions may be different or not even symmetric, unimodal and bell-shaped (i.e., not Normal). Therefore, we cannot use the Independent T-Test to test a Null-hypothesis that the centers of the two distributions (that the 2 samples came from) are identical, using this parametric test.
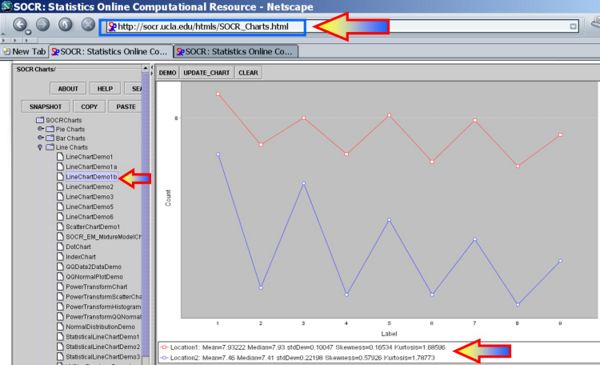
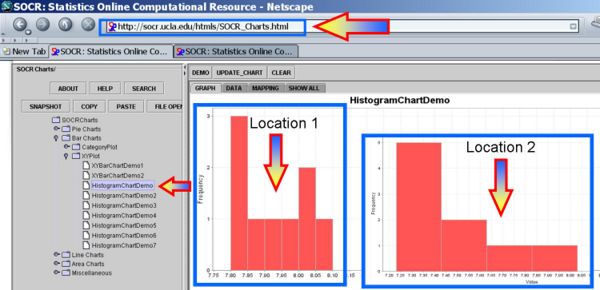
The first figure shows the index plot of the pH levels for both samples. The second figure shows the sample histograms of these samples, which are clearly not Normal-like. Therefore, the Independent T-Test would not be appropriate to analyze these data.
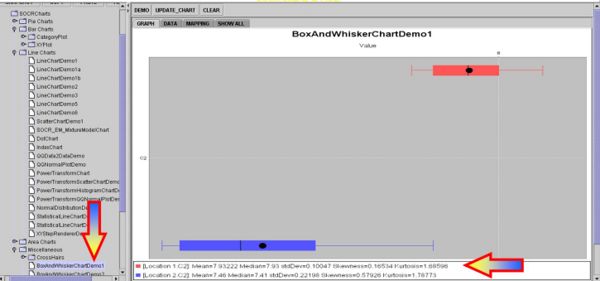
Intuitively, we may consider these group differences significantly large, especially if we look at the Box-and-Whisker Plots, but this is a qualitative inference that demands a more quantitative statistical analysis that can back up our intuition.
The Wilcoxon-Mann-Whitney Test
The Wilcoxon-Mann-Whitney (WMW) Test (also known as Mann-Whitney U Test, Mann-Whitney-Wilcoxon Test, or Wilcoxon Rank-Sum Test) is a non-parametric test for assessing whether two samples come from the same distribution. The null hypothesis is that the two samples are drawn from a single population, and therefore that their probability distributions are equal. It requires that the two samples are independent, and that the observations are ordinal or continuous measurements.
Calculations
The U statistic for the WMW test may be approximated for sample sizes above about 20 using the Normal Distribution.
The U test is provided as part of SOCR Analyses - see this activity.
For small samples, we can directly compute the WMW test-statistic as follows.
- Choose the sample for which the ranks seem to be smaller. Call this Sample 1, and call the other sample Sample 2.
- Taking each observation in Sample 2, count the number of observations in Sample 1 that are smaller than it (count 0.5 for any that are equal to it).
- The total of these counts is U.
For larger samples, a formula can be used:
- Arrange all the observations into a single ranked series. That is, rank all the observations without regard to which sample they come from.
- Add up the ranks in Sample 1. The sum of ranks in Sample 2 follows by calculation, since the sum of all the ranks equals N (N + 1)/2, where N is the total number of observations.
- "U" is then given by:
where n1 is the two sample size for Sample 1, and R1 is the sum of the ranks in Sample 1.
- Note that there is no specification as to which sample is considered Sample 1. An equally valid formula for U is
- The sum of the two values is then given by
- Knowing that R1 + R2 = N(N + 1)/2 and N = n1 + n2 , and doing some algebra, we find that the sum is
The maximum value of U is the product of the sample sizes for the two samples. In such a case, the "other" U would be 0.
The Wilcoxon-Mann-Whitney Test Using SOCR Analyses
It is much quicker to use SOCR Analyses to compute the statistical significance of the sign test. This SOCR Wilcoxon-Mann-Whitney Test Activity may also be helpful in understanding how to use this test in SOCR. We have the following results for the pH data above:
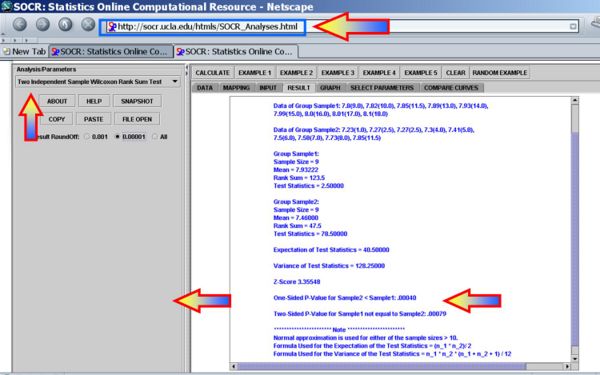
Clearly the p-value < 0.05, and therefore our data provides sufficient evidence to reject the null hypothesis. So we assumes that there were significant pH differences between the two soil lots tested in this experiment.
- One-Sided P-Value for Sample2 < Sample1: 0.00040
- Two-Sided P-Value for Sample1 not equal to Sample2: 0.00079
WMW Test vs. Independent T-Test
Both types of tests answer the same question, but treat data differently.
- The WMW test uses rank ordering
- Positive: Doesn’t depend on normality or population parameters
- Negative: Distribution free lacks power because it doesn't use all the info in the data
- The T-test uses the raw measurements
- Positive: Incorporates all of the data into calculations
- Negative: Must meet normality assumption
- Neither test is uniformly superior. If the data are normally distributed we use the T-test. If the data are not normal use the WMW test.
Practice Examples
Urinary Fluoride Concentration in Cattle
The urinary fluoride concentration (ppm) was measured both for a sample of livestock grazing in an area previously exposed to fluoride pollution and also for a similar sample of livestock grazing in an unpolluted area.
| Polluted | Unpolluted |
| 21.3 | 10.1 |
| 18.7 | 18.3 |
| 21.4 | 17.2 |
| 17.1 | 18.4 |
| 11.1 | 20.0 |
| 20.9 | |
| 19.7 |
References
- SOCR Home page: http://www.socr.ucla.edu
Translate this page: