AP Statistics Curriculum 2007 NonParam 2MedianPair
From Socr
| Line 1: | Line 1: | ||
| - | [[AP_Statistics_Curriculum_2007 | General Advance-Placement (AP) Statistics Curriculum]] - | + | [[AP_Statistics_Curriculum_2007 | General Advance-Placement (AP) Statistics Curriculum]] - Differences of Medians of Two Paired Samples |
| + | |||
| + | Distribution-free (or non-parametric) statistical methods provide alternative to the (standard) [[EBook#Chapter_VIII:_Hypothesis_Testing | parametric tests that we saw earlier]], and are applicable when the distribution of the data is unknown. | ||
| + | |||
| + | ==Motivational Clinical Example== | ||
| + | Whitley and Ball reported <ref>{{cite conference | author= Whitley, E. and Ball, J.| title=Statistics review 6: Nonparametric methods | booktitle= | ||
| + | Crit Care. 2002; 6(6): 509–513 | year=2002 | url=http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=153434}}</ref> on the relative risk of mortality from 16 studies of septic patients. The outcome measure of interest was whether the patients developed complications of acute renal failure. The relative risk calculated in each study compared the risk of dying between patients ''with'' and ''without'' renal failure. A relative risk of 1.0 means no effect, and relative risk <math>\not= 1</math> suggests beneficial or detrimental effect of developing acute renal failure in sepsis. The main goal of the study was to assess the ''cummulative evidence'' in these 16 studies to determine whether developing acute renal failure as a complication of sepsis impacts patient mortality. The data of this study is included below. | ||
| + | |||
| + | <center> | ||
| + | {| class="wikitable" style="text-align:center; width:75%" border="1" | ||
| + | |- | ||
| + | | '''Study''' || '''Relative Risk''' || '''Sign''' (Relative Risk - 1) | ||
| + | |- | ||
| + | | 1 || 0.75 || - | ||
| + | |- | ||
| + | | 2 || 2.03 || + | ||
| + | |- | ||
| + | | 3 || 2.29 || + | ||
| + | |- | ||
| + | | 4 || 2.11 || + | ||
| + | |- | ||
| + | | 5 || 0.80 || - | ||
| + | |- | ||
| + | | 6 || 1.50 || + | ||
| + | |- | ||
| + | | 7 || 0.79 || - | ||
| + | |- | ||
| + | | 8 || 1.01 || + | ||
| + | |- | ||
| + | | 9 || 1.23 || + | ||
| + | |- | ||
| + | | 10 || 1.48 || + | ||
| + | |- | ||
| + | | 11 || 2.45 || + | ||
| + | |- | ||
| + | | 12 || 1.02 || + | ||
| + | |- | ||
| + | | 13 || 1.03 || + | ||
| + | |- | ||
| + | | 14 || 1.30 || + | ||
| + | |- | ||
| + | | 15 || 1.54 || + | ||
| + | |- | ||
| + | | 16 || 1.27 || + | ||
| + | |} | ||
| + | </center> | ||
| + | |||
| + | We see the clear analogy of this study design to the [[AP_Statistics_Curriculum_2007_Infer_2Means_Dep |paired or one-sample studies]] we saw before. However, if we were to plot these data (Relative Risk) we can see that their distribution is hardly symmetric, unimodal and bell-shaped (i.e., not Normal). Therefore, we can not use the [[AP_Statistics_Curriculum_2007_Infer_2Means_Dep |paired T-test]] to test a Null-hypothesis that the mean Relative risk is 1 using this parametric test. | ||
| + | |||
| + | <center>[[Image:SOCR_EBook_Dinov_NonParam_SignTest_022308_Fig1.jpg|600px]]</center> | ||
| - | |||
| - | |||
==Approach== | ==Approach== | ||
| Line 22: | Line 69: | ||
==References== | ==References== | ||
| - | + | <references/> | |
<hr> | <hr> | ||
Revision as of 05:36, 24 February 2008
General Advance-Placement (AP) Statistics Curriculum - Differences of Medians of Two Paired Samples
Distribution-free (or non-parametric) statistical methods provide alternative to the (standard) parametric tests that we saw earlier, and are applicable when the distribution of the data is unknown.
Contents |
Motivational Clinical Example
Whitley and Ball reported <ref>Template:Cite conference</ref> on the relative risk of mortality from 16 studies of septic patients. The outcome measure of interest was whether the patients developed complications of acute renal failure. The relative risk calculated in each study compared the risk of dying between patients with and without renal failure. A relative risk of 1.0 means no effect, and relative risk 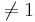 suggests beneficial or detrimental effect of developing acute renal failure in sepsis. The main goal of the study was to assess the cummulative evidence in these 16 studies to determine whether developing acute renal failure as a complication of sepsis impacts patient mortality. The data of this study is included below.
suggests beneficial or detrimental effect of developing acute renal failure in sepsis. The main goal of the study was to assess the cummulative evidence in these 16 studies to determine whether developing acute renal failure as a complication of sepsis impacts patient mortality. The data of this study is included below.
| Study | Relative Risk | Sign (Relative Risk - 1) |
| 1 | 0.75 | - |
| 2 | 2.03 | + |
| 3 | 2.29 | + |
| 4 | 2.11 | + |
| 5 | 0.80 | - |
| 6 | 1.50 | + |
| 7 | 0.79 | - |
| 8 | 1.01 | + |
| 9 | 1.23 | + |
| 10 | 1.48 | + |
| 11 | 2.45 | + |
| 12 | 1.02 | + |
| 13 | 1.03 | + |
| 14 | 1.30 | + |
| 15 | 1.54 | + |
| 16 | 1.27 | + |
We see the clear analogy of this study design to the paired or one-sample studies we saw before. However, if we were to plot these data (Relative Risk) we can see that their distribution is hardly symmetric, unimodal and bell-shaped (i.e., not Normal). Therefore, we can not use the paired T-test to test a Null-hypothesis that the mean Relative risk is 1 using this parametric test.
Approach
TBD
Model Validation
TBD
Computational Resources: Internet-based SOCR Tools
TBD
Examples
TBD
Hands-on Activities
TBD
References
<references/>
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:
