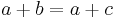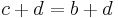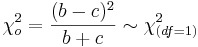AP Statistics Curriculum 2007 NonParam 2PropIndep
From Socr
(→ General Advance-Placement (AP) Statistics Curriculum - Two-Samples Difference of Proportions) |
|||
| (7 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
| - | + | ==[[AP_Statistics_Curriculum_2007 | General Advance-Placement (AP) Statistics Curriculum]] - Two-Samples Difference of Proportions== | |
===Differences of Proportions of Two Independent Samples=== | ===Differences of Proportions of Two Independent Samples=== | ||
If the samples are independent and we are interested in the differences in the proportions of subjects of the same trait (a characteristic of each observation, e.g., gender) we need to use the [[AP_Statistics_Curriculum_2007_Hypothesis_Proportion | standard proportion tests]] | If the samples are independent and we are interested in the differences in the proportions of subjects of the same trait (a characteristic of each observation, e.g., gender) we need to use the [[AP_Statistics_Curriculum_2007_Hypothesis_Proportion | standard proportion tests]] | ||
| - | : For small sample-sizes, we use corrected-proportions (<math>\tilde{p}</math>) that we saw in the [[AP_Statistics_Curriculum_2007_Hypothesis_Proportion | | + | : For small sample-sizes, we use corrected-proportions (<math>\tilde{p}</math>) that we saw in the [[AP_Statistics_Curriculum_2007_Hypothesis_Proportion | ''Independent Sample Tests for Proportions'' section]]. |
| - | : For large samples, we can use the raw-sample proportion (<math>\hat{p}</math>) as in the [[AP_Statistics_Curriculum_2007_Hypothesis_Proportion | | + | : For large samples, we can use the raw-sample proportion (<math>\hat{p}</math>) as in the [[AP_Statistics_Curriculum_2007_Hypothesis_Proportion | ''Independent Sample Tests for Proportions'' section]]. |
===Differences of Proportions of Two Paired-Samples=== | ===Differences of Proportions of Two Paired-Samples=== | ||
| Line 20: | Line 20: | ||
| <math>D^+</math> || <math>D^-</math>|| '''Total''' | | <math>D^+</math> || <math>D^-</math>|| '''Total''' | ||
|- | |- | ||
| - | | rowspan=3| ''' | + | | rowspan=3| '''After Treatment''' || <math>D^+</math> || a=101 || b=59 || a+b=160 |
|- | |- | ||
| <math>D^-</math> || c=121 || d=33 || c+d=154 | | <math>D^-</math> || c=121 || d=33 || c+d=154 | ||
| Line 28: | Line 28: | ||
</center> | </center> | ||
| - | '''Marginal homogeneity''' occurs when the row totals | + | '''Marginal homogeneity''' occurs when the row totals equal to the column totals, ''a'' and ''d'' in each equation can be cancelled; leaving ''b'' equal to ''c'': |
:<math>a+b = a+c \,</math> | :<math>a+b = a+c \,</math> | ||
| Line 39: | Line 39: | ||
:<math>\chi_o^2 = {(b-c)^2 \over b+c} \sim \chi_{(df=1)}^2</math> | :<math>\chi_o^2 = {(b-c)^2 \over b+c} \sim \chi_{(df=1)}^2</math> | ||
| - | The marginal frequencies are not homogeneous if the <math>\chi^2</math> result is significant ''p'' < 0.05. If ''b'' and/or ''c'' are small (''b'' + ''c'' < 20) then <math>\chi^2</math> is not approximated by the Chi- | + | The marginal frequencies are not homogeneous if the <math>\chi^2</math> result is significant ''p'' < 0.05. If ''b'' and/or ''c'' are small (''b'' + ''c'' < 20) then <math>\chi^2</math> is not approximated by the Chi-Square Distribution and a [[AP_Statistics_Curriculum_2007_NonParam_2MedianPair | Sign Test]] should instead be used. |
An interesting observation when interpreting McNemar's test is that the elements of the main diagonal contribute no information whatsoever to the decision if (in the above example) pre- or post-treatment condition is more favorable. | An interesting observation when interpreting McNemar's test is that the elements of the main diagonal contribute no information whatsoever to the decision if (in the above example) pre- or post-treatment condition is more favorable. | ||
| - | < | + | ===General McNemar test of marginal homogeneity for a single category=== |
| + | If we have observed measurements on a K-level categorical variable -- e.g., agreement between two evaluators summarized by a K×K classification table, where each row or column contains the number of individuals rated as part of this group by each evaluator. For instance, two instructors may evaluate students as 1=poor, 2=good and 3=excellent. There could be significant differences in the evaluations of the same students by the 2 instructors. Suppose we are interested in whether the proportions of students rated ''excellent'' by the 2 instructors are the same. Then we'll pool the ''poor'' and ''good'' categories together and form a 2x2 table that we can then use the 2x2 McNemar test statistics on, as shown below. | ||
| + | |||
| + | <center> | ||
| + | {| class="wikitable" title="Title1" style="text-align:center; width:35%" border="1" | ||
| + | |- | ||
| + | | || || colspan="4" align="center"| Evaluator 2 | ||
| + | |- | ||
| + | | || || Poor || Good || Excellent || Total | ||
| + | |- | ||
| + | | rowspan=4 | Evaluator 1 || Poor || 5 || 15 || 4 || 24 | ||
| + | |- | ||
| + | | Good || 16 || 10 || 9 || 35 | ||
| + | |- | ||
| + | | Excellent || 11 || 17 || 13 || 41 | ||
| + | |- | ||
| + | | Total || 32 || 42 || 26 || 100 | ||
| + | |} | ||
| + | |||
| + | {| class="wikitable" title="Title2" style="text-align:center; width:35%" border="1" | ||
| + | |- | ||
| + | | || || colspan="3" align="center"|Evaluator 2 | ||
| + | |- | ||
| + | | || || Poor || Good or Excellent || Total | ||
| + | |- | ||
| + | | rowspan=3 | Evaluator 1 || Poor || a=5 || b=19 || a+b=24 | ||
| + | |- | ||
| + | | Good or Excellent || c=27 || d=49 || c+d=76 | ||
| + | |- | ||
| + | | Total || a+c=32 || b+d=68 || a+b+c+d=100 | ||
| + | |} | ||
| + | </center> | ||
| + | |||
| + | To test '''marginal homogeneity''' for one single category (in this case ''poor evaluation'') means to test row/column marginal homogeneity for the first category (poor). This is achieved by collapsing all rows and columns corresponding to the other categories. | ||
| + | |||
| + | : <math>x_o^2 = {(b-c)^2 \over b+c} = {(-8)^2 \over 46} = 1.39 \sim \chi_{(df=1)}^2</math> | ||
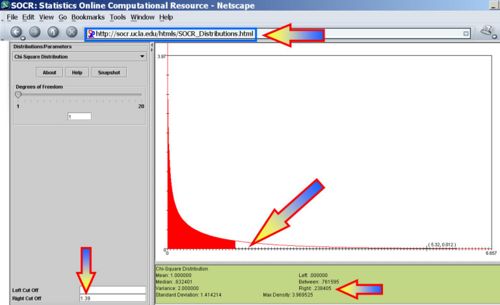
| + | : <math>P(\chi_{(df=1)}^2 > 1.39) = 0.238405</math> and therefore, we do not have sufficient evidence to reject a hull hypotheses that the 2 evaluators were consistent in their ratings of students. | ||
| + | |||
| + | <center>[[Image:SOCR_EBook_Dinov_NonParam_McNemar_041408_Fig1.jpg|500px]]</center> | ||
==References== | ==References== | ||
Current revision as of 17:35, 28 June 2010
Contents |
General Advance-Placement (AP) Statistics Curriculum - Two-Samples Difference of Proportions
Differences of Proportions of Two Independent Samples
If the samples are independent and we are interested in the differences in the proportions of subjects of the same trait (a characteristic of each observation, e.g., gender) we need to use the standard proportion tests
- For small sample-sizes, we use corrected-proportions (
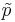 ) that we saw in the Independent Sample Tests for Proportions section.
) that we saw in the Independent Sample Tests for Proportions section.
- For large samples, we can use the raw-sample proportion (
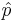 ) as in the Independent Sample Tests for Proportions section.
) as in the Independent Sample Tests for Proportions section.
Differences of Proportions of Two Paired-Samples
If the samples are paired, then we can employ the McNemar's non-parametric test for differences in proportions in matched pair samples. It is most often used when the observed variable is a dichotomous variable (presence or absence of a trait/characteristic for each observation).
Example
Suppose a medical doctor is interested in determining the effect of a drug on a particular disease (D). Suppose the doctor conducts a study and records the frequencies of incidence of the disease (D + and D − ) in a random population before the treatment with the new drug takes place. Then the doctor prescribes the treatment to all subjects and records the incidence of the disease in the rows following the treatment. The test requires the same subjects to be included in the before- and after-treatment measurements (matched pairs).
| Before Treatment | ||||
| D + | D − | Total | ||
| After Treatment | D + | a=101 | b=59 | a+b=160 |
| D − | c=121 | d=33 | c+d=154 | |
| Total | a+c=222 | b+d=92 | a+b+c+d=314 | |
Marginal homogeneity occurs when the row totals equal to the column totals, a and d in each equation can be cancelled; leaving b equal to c:
In this example, marginal homogeneity would mean there was no effect of the treatment.
- The McNemar statistic is shown below:
The marginal frequencies are not homogeneous if the χ2 result is significant p < 0.05. If b and/or c are small (b + c < 20) then χ2 is not approximated by the Chi-Square Distribution and a Sign Test should instead be used.
An interesting observation when interpreting McNemar's test is that the elements of the main diagonal contribute no information whatsoever to the decision if (in the above example) pre- or post-treatment condition is more favorable.
General McNemar test of marginal homogeneity for a single category
If we have observed measurements on a K-level categorical variable -- e.g., agreement between two evaluators summarized by a K×K classification table, where each row or column contains the number of individuals rated as part of this group by each evaluator. For instance, two instructors may evaluate students as 1=poor, 2=good and 3=excellent. There could be significant differences in the evaluations of the same students by the 2 instructors. Suppose we are interested in whether the proportions of students rated excellent by the 2 instructors are the same. Then we'll pool the poor and good categories together and form a 2x2 table that we can then use the 2x2 McNemar test statistics on, as shown below.
| Evaluator 2 | |||||
| Poor | Good | Excellent | Total | ||
| Evaluator 1 | Poor | 5 | 15 | 4 | 24 |
| Good | 16 | 10 | 9 | 35 | |
| Excellent | 11 | 17 | 13 | 41 | |
| Total | 32 | 42 | 26 | 100 | |
| Evaluator 2 | ||||
| Poor | Good or Excellent | Total | ||
| Evaluator 1 | Poor | a=5 | b=19 | a+b=24 |
| Good or Excellent | c=27 | d=49 | c+d=76 | |
| Total | a+c=32 | b+d=68 | a+b+c+d=100 | |
To test marginal homogeneity for one single category (in this case poor evaluation) means to test row/column marginal homogeneity for the first category (poor). This is achieved by collapsing all rows and columns corresponding to the other categories.
-
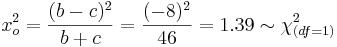
-
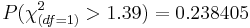 and therefore, we do not have sufficient evidence to reject a hull hypotheses that the 2 evaluators were consistent in their ratings of students.
and therefore, we do not have sufficient evidence to reject a hull hypotheses that the 2 evaluators were consistent in their ratings of students.
References
- SOCR Home page: http://www.socr.ucla.edu
Translate this page: