AP Statistics Curriculum 2007 NonParam ANOVA
From Socr
(→Motivational Example) |
(→The Kruskal-Wallis Test) |
||
| Line 26: | Line 26: | ||
==The Kruskal-Wallis Test== | ==The Kruskal-Wallis Test== | ||
| - | '''Kruskal-Wallis | + | '''Kruskal-Wallis One-Way Analysis of Variance''' by ranks is a non-parametric method for testing equality of two or more population medians. Intuitively, it is identical to a [[AP_Statistics_Curriculum_2007_ANOVA_1Way | One-Way Analysis of Variance]] with the raw data (observed measurements) replaced by their ranks. |
| - | Since it is a non-parametric method, the Kruskal-Wallis | + | Since it is a non-parametric method, the Kruskal-Wallis Test '''does not''' assume a normal population, unlike the analogous one-way ANOVA. However, the test does assume identically-shaped distributions for all groups, except for any difference in their centers (e.g., medians). |
==Calculations== | ==Calculations== | ||
Revision as of 23:11, 10 March 2008
Contents |
General Advance-Placement (AP) Statistics Curriculum - Means of Several Independent Samples
In this section we extend the multi-sample inference which we discussed in the ANOVA section, to the situation where the ANOVA assumptions are invalid. Hence we use a non-parametric analysis to study differences in centrality between two or more populations.
Motivational Example
Suppose four groups of students were randomly assigned to be taught with four different techniques, and their achievement test scores were recorded. Are the distributions of test scores the same, or do they differ in location? The data is presented in the table below.
| Teaching Method | ||||
| Method 1 | Method 2 | Method 3 | Method 4 | |
| Index | 65 | 75 | 59 | 94 |
| 87 | 69 | 78 | 89 | |
| 73 | 83 | 67 | 80 | |
| 79 | 81 | 62 | 88 | |
The small sample sizes and the lack of distribution information of each sample illustrate how ANOVA may not be appropriate for analyzing these types of data.
The Kruskal-Wallis Test
Kruskal-Wallis One-Way Analysis of Variance by ranks is a non-parametric method for testing equality of two or more population medians. Intuitively, it is identical to a One-Way Analysis of Variance with the raw data (observed measurements) replaced by their ranks.
Since it is a non-parametric method, the Kruskal-Wallis Test does not assume a normal population, unlike the analogous one-way ANOVA. However, the test does assume identically-shaped distributions for all groups, except for any difference in their centers (e.g., medians).
Calculations
Let N be the total number of observations, then 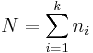 .
.
Let R(Xij) denote the rank assigned to Xij and let Ri be the sum of ranks assigned to the ith sample.
-
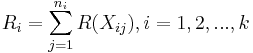 .
.
The SOCR program computes Ri for each sample. The test statistic is defined for the following formulation of hypotheses:
- Ho: All of the k population distribution functions are identical.
- H1: At least one of the populations tends to yield larger observations than at least one of the other populations.
Suppose {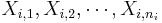 } represents the values of the ith sample, where
} represents the values of the ith sample, where 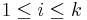 .
.
- Test statistics:
- T =
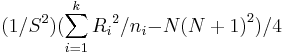 ,
,
- T =
where
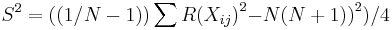 .
.
- Note: If there are no ties, then the test statistic is reduced to:
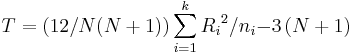 .
.
\end{center}
However, the SOCR implementation allows for the possibility of having ties; so it uses the non-simplified, exact method of computation.
Multiple comparisons have to be done here. For each pair of groups, the following is computed and printed at the Result Panel.
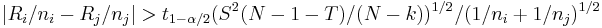 .
.
The SOCR computation employs the exact method instead of the approximate one (Conover 1980), since computation is easy and fast to implement and the exact method is somewhat more accurate.
The Kruskal-Wallis Test using SOCR Analyses
It is much quicker to use SOCR Analyses to compute the statistical significance of this test. This SOCR KruskalWallis Test activity may also be helpful in understanding how to use this test in SOCR.
For the teaching-methods example above, we can easily compute the statistical significance of the differences between the group medians (centers):
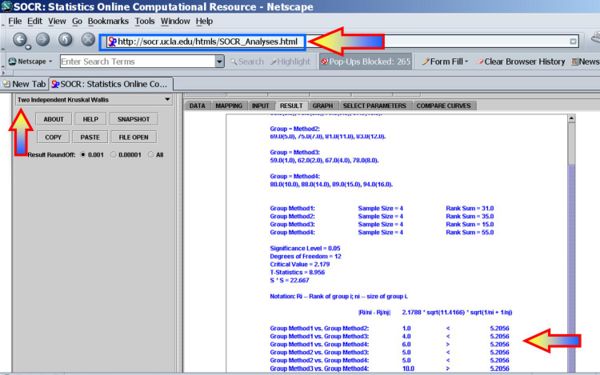
Clearly, there is only one significant group difference between medians, after the multiple testing correction, for the group1 vs. group4 comparison (see below):
- Group Method1 vs. Group Method2: 1.0 < 5.2056
- Group Method1 vs. Group Method3: 4.0 < 5.2056
- Group Method1 vs. Group Method4: 6.0 > 5.2056
- Group Method2 vs. Group Method3: 5.0 < 5.2056
- Group Method2 vs. Group Method4: 5.0 < 5.2056
- Group Method3 vs. Group Method4: 10.0 > 5.2056
Practice Examples
TBD
Notes
- The Friedman Fr test is the rank equivalent of the randomized block design alternative to the two-way analysis of variance F test. The SOCR Friedman Test activity demonstrates how to use SOCR Analyses to compute the Friedman test statistics and p-value.
References
Conover W (1980). Practical Nonparametric Statistics. John Wiley & Sons, New York, second edition.
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:
