AP Statistics Curriculum 2007 NonParam ANOVA
From Socr
Contents |
General Advance-Placement (AP) Statistics Curriculum - Means of Several Independent Samples
In this section we extend the multi-sample inference which we discussed in the ANOVA section, to the situation where the ANOVA assumptions are invalid. Hence we use a non-parametric analysis to study differences in centrality between two or more populations.
Motivational Example
Suppose four groups of students were randomly assigned to be taught with four different techniques, and their achievement test scores were recorded. Are the distributions of test scores the same, or do they differ in location? The data is presented in the table below.
| Teaching Method | ||||
| Method 1 | Method 2 | Method 3 | Method 4 | |
| Index | 65 | 75 | 59 | 94 |
| 87 | 69 | 78 | 89 | |
| 73 | 83 | 67 | 80 | |
| 79 | 81 | 62 | 88 | |
The small sample sizes, and the lack of information about the distribution of each of the four samples, imply that ANOVA may not be appropriate for analyzing these data.
The Kruskal-Wallis Test
Kruskal-Wallis one-way analysis of variance by ranks is a non-parametric method for testing equality of two or more population medians. Intuitively, it is identical to a one-way analysis of variance with the raw data (observed measurements) replaced by their ranks.
Since it is a non-parametric method, the Kruskal-Wallis test does not assume a normal population, unlike the analogous one-way ANOVA. However, the test does assume identically-shaped distributions for all groups, except for any difference in their centers (e.g., medians).
Calculations
- Rank all data from all groups together; i.e., rank the data from 1 to N ignoring group membership. Assign any tied values the average of the ranks they would have received had they not been tied.
- The test statistic is given by:
-
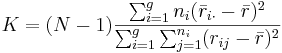 , where:
, where:
- ng is the number of observations in group g
- rij is the rank (among all observations) of observation j from group i
- N is the total number of observations across all groups
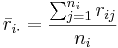 ,
,
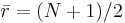 is the average of all the rij.
is the average of all the rij.
- Notice that the denominator of the expression for K is exactly (N − 1)N(N + 1) / 12. Thus
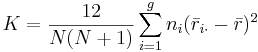 .
.
- A correction for ties can be made by dividing K by
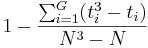 , where G is the number of groupings of different tied ranks, and ti is the number of tied values within group i that are tied at a particular value. This correction usually makes little difference in the value of K unless there are a large number of ties.
, where G is the number of groupings of different tied ranks, and ti is the number of tied values within group i that are tied at a particular value. This correction usually makes little difference in the value of K unless there are a large number of ties.
- Finally, the p-value is approximated by
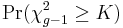 . If some ni's are small (i.e., less than 5) the probability distribution of K can be quite different from this Chi-square distribution.
. If some ni's are small (i.e., less than 5) the probability distribution of K can be quite different from this Chi-square distribution.
The null hypothesis of equal population medians would then be rejected if 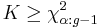 .
.
The Kruskal-Wallis Test using SOCR Analyses
It is much quicker to use SOCR Analyses to compute the statistical significance of this test. This SOCR KruskalWallis Test activity may also be helpful in understanding how to use this test in SOCR.
For the teaching-methods example above, we can easily compute the statistical significance of the differences between the group medians (centers):
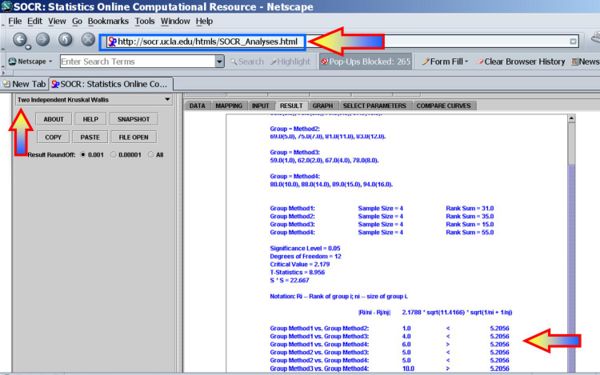
Clearly, there are significant differences between the group medians, even after the multiple testing correction, all groups appear different from each other.
- Group Method1 vs. Group Method2: 1.0 < 5.2056
- Group Method1 vs. Group Method3: 4.0 < 5.2056
- Group Method1 vs. Group Method4: 6.0 > 5.2056
- Group Method2 vs. Group Method3: 5.0 < 5.2056
- Group Method2 vs. Group Method4: 5.0 < 5.2056
- Group Method3 vs. Group Method4: 10.0 > 5.2056
Practice Examples
TBD
Notes
- The Friedman Fr test is the rank equivalent of the randomized block design alternative to the two-way analysis of variance F test.
References
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:
