AP Statistics Curriculum 2007 NonParam VarIndep
From Socr
(→See also) |
|||
| (6 intermediate revisions not shown) | |||
| Line 2: | Line 2: | ||
==Differences of Variances of Independent Samples== | ==Differences of Variances of Independent Samples== | ||
| - | It is frequently necessary to test if ''k'' samples have equal variances. | + | It is frequently necessary to test if ''k'' samples have equal variances. ''Homogeneity of variances'' is often a reference to equal variances across samples. Some statistical tests, for example the [[AP_Statistics_Curriculum_2007_ANOVA_1Way | analysis of variance]], assume that variances are equal across groups or samples. |
==Approach== | ==Approach== | ||
| - | The (modified) Fligner-Killeen test provides the means for studying the homogeneity of variances of ''k'' populations { <math>X_{i,j}</math>, for <math>1\leq i \leq n_j</math> and <math>1\leq j \leq k</math>}. The test jointly ranks the absolute values of <math>|X_{i,j}-\tilde{X_j}|</math> and assigns increasing '''scores''' <math>a_{N,i}=\Phi^{-1}({1 + {i\over N+1} \over 2})</math>, based on the ranks of all observations, see the Conover, Johnson, and Johnson (1981) reference below. | + | The (modified) Fligner-Killeen test provides the means for studying the homogeneity of variances of ''k'' populations { <math>X_{i,j}</math>, for <math>1\leq i \leq n_j</math> and <math>1\leq j \leq k</math>}. The test jointly ranks the absolute values of <math>|X_{i,j}-\tilde{X_j}|</math> and assigns increasing '''scores''' <math>a_{N,i}=\Phi^{-1}({1 + {i\over N+1} \over 2})</math>, based on the ranks of all observations, see the [[AP_Statistics_Curriculum_2007_NonParam_VarIndep#References | Conover, Johnson, and Johnson (1981) reference below]]. |
In this test, <math>\tilde{X_j}</math> is the sample median of the ''j<sup>th</sup>'' population, and <math>\Phi(.)</math> is the [[AP_Statistics_Curriculum_2007_Normal_Std | cumulative distribution function for Normal distribution]]. The Fligner-Killeen test is sometimes also called the ''median-centering Fligner-Killeen test''. | In this test, <math>\tilde{X_j}</math> is the sample median of the ''j<sup>th</sup>'' population, and <math>\Phi(.)</math> is the [[AP_Statistics_Curriculum_2007_Normal_Std | cumulative distribution function for Normal distribution]]. The Fligner-Killeen test is sometimes also called the ''median-centering Fligner-Killeen test''. | ||
| Line 11: | Line 11: | ||
* '''Fligner-Killeen test statistics''': | * '''Fligner-Killeen test statistics''': | ||
: <math>x_o^2 = {\sum_{j=1}^k {n_j(\bar{A_j} -\bar{a})^2} \over V^2}</math>, | : <math>x_o^2 = {\sum_{j=1}^k {n_j(\bar{A_j} -\bar{a})^2} \over V^2}</math>, | ||
| - | : where <math>\bar{A_j}</math> is the mean score for the ''j<sup>th</sup>'' sample, | + | : where <math>\bar{A_j}</math> is the mean score for the ''j<sup>th</sup>'' sample, <math>\bar{a}</math> is the overall mean score of all <math>a_{N,i}</math>, and <math>V^2</math> is the sample variance of all scores. |
That is: | That is: | ||
: <math>N=\sum_{j=1}^k{n_j}</math>, | : <math>N=\sum_{j=1}^k{n_j}</math>, | ||
| - | : <math>\bar{A_j} = {1\over n_j}\sum_{i=1}^{n_j}{a_{N,m_i}}</math>, | + | : <math>\bar{A_j} = {1\over n_j}\sum_{i=1}^{n_j}{a_{N,m_i}}</math>, where <math>a_{N,m_i}</math> is the increasing rank score for the ''i<sup>th</sup>''-observation in the ''j<sup>th</sup>''-sample, |
: <math>\bar{a} = {1\over N}\sum_{i=1}^{N}{a_{N,i}}</math>, | : <math>\bar{a} = {1\over N}\sum_{i=1}^{N}{a_{N,i}}</math>, | ||
: <math>V^2 = {1\over N-1}\sum_{i=1}^{N}{(a_{N,i}-\bar{a})^2}</math>. | : <math>V^2 = {1\over N-1}\sum_{i=1}^{N}{(a_{N,i}-\bar{a})^2}</math>. | ||
| Line 27: | Line 27: | ||
==Computational Resources: Internet-based SOCR Tools== | ==Computational Resources: Internet-based SOCR Tools== | ||
| - | + | * See the [http://www.socr.ucla.edu/htmls/ana/FlignerKilleen_Analysis.html SOCR Fligner-Killeen Analysis applet]. | |
| + | * See the [[SOCR_EduMaterials_AnalysisActivities_FlignerKilleen | SOCR Fligner-Killeen Activity]]. | ||
==Examples== | ==Examples== | ||
Suppose we wanted to study whether the variances in certain time period (e.g., 1981 to 2006) of the consumer-price-indices (CPI) of several items were significantly different. We can use the [[SOCR_Data_Dinov_021808_ConsumerPriceIndex | SOCR CPI Dataset]] to answer this question for the '''Fuel''', '''Oil''', '''Bananas''', '''Tomatoes''', '''Orange Juice''', '''Beef''' and '''Gasoline''' items. | Suppose we wanted to study whether the variances in certain time period (e.g., 1981 to 2006) of the consumer-price-indices (CPI) of several items were significantly different. We can use the [[SOCR_Data_Dinov_021808_ConsumerPriceIndex | SOCR CPI Dataset]] to answer this question for the '''Fuel''', '''Oil''', '''Bananas''', '''Tomatoes''', '''Orange Juice''', '''Beef''' and '''Gasoline''' items. | ||
| + | |||
| + | ==See also== | ||
| + | * [[SOCR_EduMaterials_AnalysisActivities_FlignerKilleen | SOCR Fligner-Killeen Activity]] provides more hands-on examples. | ||
| + | * [[AP_Statistics_Curriculum_2007_Infer_BiVar | Parametric Variance Homogeneity test]]. | ||
| + | * [http://www.socr.ucla.edu/htmls/ana/FlignerKilleen_Analysis.html SOCR Fligner-Killeen Applet]. | ||
<hr> | <hr> | ||
Current revision as of 02:30, 29 November 2008
General Advance-Placement (AP) Statistics Curriculum - Variances of Two Independent Samples
Contents |
Differences of Variances of Independent Samples
It is frequently necessary to test if k samples have equal variances. Homogeneity of variances is often a reference to equal variances across samples. Some statistical tests, for example the analysis of variance, assume that variances are equal across groups or samples.
Approach
The (modified) Fligner-Killeen test provides the means for studying the homogeneity of variances of k populations { Xi,j, for 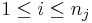 and
and 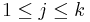 }. The test jointly ranks the absolute values of
}. The test jointly ranks the absolute values of 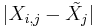 and assigns increasing scores
and assigns increasing scores 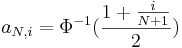 , based on the ranks of all observations, see the Conover, Johnson, and Johnson (1981) reference below.
, based on the ranks of all observations, see the Conover, Johnson, and Johnson (1981) reference below.
In this test, 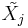 is the sample median of the jth population, and Φ(.) is the cumulative distribution function for Normal distribution. The Fligner-Killeen test is sometimes also called the median-centering Fligner-Killeen test.
is the sample median of the jth population, and Φ(.) is the cumulative distribution function for Normal distribution. The Fligner-Killeen test is sometimes also called the median-centering Fligner-Killeen test.
- Fligner-Killeen test statistics:
-
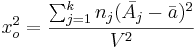 ,
,
- where
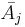 is the mean score for the jth sample,
is the mean score for the jth sample, 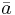 is the overall mean score of all aN,i, and V2 is the sample variance of all scores.
is the overall mean score of all aN,i, and V2 is the sample variance of all scores.
That is:
-
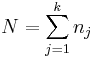 ,
,
-
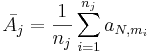 , where
, where 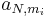 is the increasing rank score for the ith-observation in the jth-sample,
is the increasing rank score for the ith-observation in the jth-sample,
-
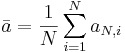 ,
,
-
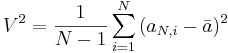 .
.
- Fligner-Killeen probabilities:
For large sample sizes, the modified Fligner-Killeen test statistic has an asymptotic chi-square distribution with (k-1) degrees of freedom
-
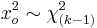 .
.
- Note:
- Conover, Johnson, and Johnson (1981) carried a simulation comparing different variance homogeneity tests and reported that the modified Fligner-Killeen test is most robust against departures from normality.
Computational Resources: Internet-based SOCR Tools
- See the SOCR Fligner-Killeen Analysis applet.
- See the SOCR Fligner-Killeen Activity.
Examples
Suppose we wanted to study whether the variances in certain time period (e.g., 1981 to 2006) of the consumer-price-indices (CPI) of several items were significantly different. We can use the SOCR CPI Dataset to answer this question for the Fuel, Oil, Bananas, Tomatoes, Orange Juice, Beef and Gasoline items.
See also
- SOCR Fligner-Killeen Activity provides more hands-on examples.
- Parametric Variance Homogeneity test.
- SOCR Fligner-Killeen Applet.
Alternative tests of Variance Homogeneity
References
- Conover, W. J., Johnson, M.E., and Johnson M. M. (1981), A comparative study of tests for homogeneity of variances, with applications to the outer continental shelf bidding data. Technometrics 23, 351-361.
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:
