AP Statistics Curriculum 2007 Normal Critical
From Socr
m (→Textbook Prices) |
|||
| (12 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
| - | ==[[AP_Statistics_Curriculum_2007 | General Advance-Placement (AP) Statistics Curriculum]] - | + | ==[[AP_Statistics_Curriculum_2007 | General Advance-Placement (AP) Statistics Curriculum]] - Non-Standard Normal Distribution and Experiments: Finding Critical Values== |
| - | === | + | === Non-Standard Normal Distribution and Experiments: Finding Scores (Critical Values)=== |
| - | + | In addition to being able to [[AP_Statistics_Curriculum_2007_Normal_Prob | compute probability (p) values]], we often need to estimate the critical values of the Normal Distribution for a given p-value. | |
| - | + | ||
| - | == | + | * The back and forth linear transformations converting between Standard and General Normal Distributions are always useful in such analyses (Let ''X'' denotes General (<math>X\sim N(\mu,\sigma^2)</math>) and ''Z'' denotes Standard (<math>Z\sim N(0,1)</math>) Normal random variables): |
| - | + | : <math>Z = {X-\mu \over \sigma}</math> converts general normal scores to standard (Z) values. | |
| + | : <math>X = \mu +Z\sigma \ </math> converts standard scores to general normal values. | ||
| - | + | ===Examples=== | |
| + | This [[Help_pages_for_SOCR_Distributions | Distributions help-page may be useful in understanding SOCR Distribution Applet]]. | ||
| - | === | + | ====[[SOCR_EduMaterials_Activities_Normal_Probability_examples | A large number of Normal distribution examples using SOCR tools is available here]]==== |
| - | + | ||
| - | + | ====Textbook Prices==== | |
| + | Suppose the amount of money that college students spend each semester on textbooks is normally distributed with a mean of $195 and a standard deviation of $20. If we ask a random college students from this population how much she spent on books this semester, what is the maximum dollar amount that would guarantee she spends only as little as 30% of the population? (<math>P(X<184.512)=0.3</math>) | ||
| + | <center>[[Image:SOCR_EBook_Dinov_RV_Normal_013108_Fig12.jpg|500px]]</center> | ||
| - | === | + | You can also do this problem exactly using the [http://socr.ucla.edu/Applets.dir/Normal_T_Chi2_F_Tables.htm SOCR high-precision Nornal Distribution Calculator]. If \(z_o=-0.5243987892920383\), then \(P(-z_o<Z<z_o)=0.4\) and \(P(Z<z_o)=0.3\). Thus, \(x_o=\mu +z_o\sigma=195+(-0.5243987892920383)*20=184.512024214159234\). |
| - | + | <center>[[Image:SOCR_EBook_Dinov_RV_Normal_013108_Fig13.jpg|500px]]</center> | |
| - | === | + | ====Human Weights and Heights==== |
| - | + | Human [http://en.wikipedia.org/wiki/Human_weight weights] and [http://en.wikipedia.org/wiki/Human_height heights] are known to be approximately Normally distributed. Look at the [[SOCR_Data_Dinov_020108_HeightsWeights |SOCR Weighs and Heights Dataset]] and use the [[SOCR_EduMaterials_Activities_Histogram_Graphs | SOCR Charts]] to validate these statements based on this sample dataset. | |
| - | * | + | * Suppose the heights of college women are approximately Normally distributed with a mean of 65 inches and a standard deviation of 2 inches. If a randomly chosen college woman is at the 10<sup>th</sup> percentile (shortest 10% for women) in height for college women, then what is the largest height closest to hers (i.e., what is her estimated height)? |
| - | + | <center>[[Image:SOCR_EBook_Dinov_RV_Normal_013108_Fig14.jpg|500px]]</center> | |
| - | + | ||
| - | + | ||
| - | + | ===[[EBook_Problems_Normal_Critical|Problems]]=== | |
<hr> | <hr> | ||
| + | |||
===References=== | ===References=== | ||
| - | * | + | * [[SOCR_EduMaterials_Activities_Histogram_Graphs | Histogram Plots]] |
| + | * [[SOCR_EduMaterials_Activities_BoxPlot | Box-and-whisker Plots]] | ||
| + | * [[SOCR_EduMaterials_Activities_DotChart |Dotplot]] | ||
| + | * [[SOCR_EduMaterials_Activities_QQChart |Quantile-Quantile Probability Plot]] | ||
| + | * [http://socr.ucla.edu/Applets.dir/Normal_T_Chi2_F_Tables.htm SOCR High-Precision Normal Distribution Calculator] | ||
<hr> | <hr> | ||
Current revision as of 15:50, 3 May 2013
Contents |
General Advance-Placement (AP) Statistics Curriculum - Non-Standard Normal Distribution and Experiments: Finding Critical Values
Non-Standard Normal Distribution and Experiments: Finding Scores (Critical Values)
In addition to being able to compute probability (p) values, we often need to estimate the critical values of the Normal Distribution for a given p-value.
- The back and forth linear transformations converting between Standard and General Normal Distributions are always useful in such analyses (Let X denotes General (
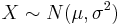 ) and Z denotes Standard (
) and Z denotes Standard (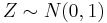 ) Normal random variables):
) Normal random variables):
-
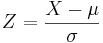 converts general normal scores to standard (Z) values.
converts general normal scores to standard (Z) values.
-
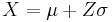 converts standard scores to general normal values.
converts standard scores to general normal values.
Examples
This Distributions help-page may be useful in understanding SOCR Distribution Applet.
A large number of Normal distribution examples using SOCR tools is available here
Textbook Prices
Suppose the amount of money that college students spend each semester on textbooks is normally distributed with a mean of $195 and a standard deviation of $20. If we ask a random college students from this population how much she spent on books this semester, what is the maximum dollar amount that would guarantee she spends only as little as 30% of the population? (P(X < 184.512) = 0.3)
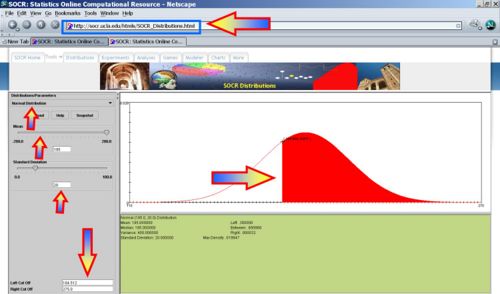
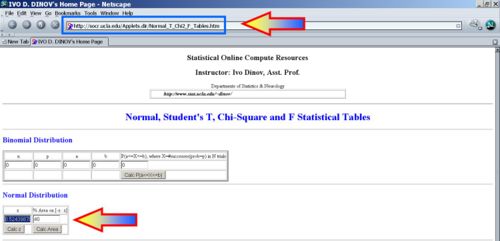
You can also do this problem exactly using the SOCR high-precision Nornal Distribution Calculator. If \(z_o=-0.5243987892920383\), then \(P(-z_o<Z<z_o)=0.4\) and \(P(Z<z_o)=0.3\). Thus, \(x_o=\mu +z_o\sigma=195+(-0.5243987892920383)*20=184.512024214159234\).
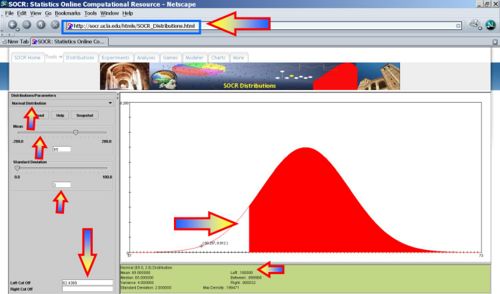
Human Weights and Heights
Human weights and heights are known to be approximately Normally distributed. Look at the SOCR Weighs and Heights Dataset and use the SOCR Charts to validate these statements based on this sample dataset.
- Suppose the heights of college women are approximately Normally distributed with a mean of 65 inches and a standard deviation of 2 inches. If a randomly chosen college woman is at the 10th percentile (shortest 10% for women) in height for college women, then what is the largest height closest to hers (i.e., what is her estimated height)?
Problems
References
- Histogram Plots
- Box-and-whisker Plots
- Dotplot
- Quantile-Quantile Probability Plot
- SOCR High-Precision Normal Distribution Calculator
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:
