AP Statistics Curriculum 2007 Normal Critical
From Socr
| Line 18: | Line 18: | ||
<center>[[Image:SOCR_EBook_Dinov_RV_Normal_013108_Fig13.jpg|500px]]</center> | <center>[[Image:SOCR_EBook_Dinov_RV_Normal_013108_Fig13.jpg|500px]]</center> | ||
| - | + | ====Human Weights and Heights==== | |
| - | + | Human [http://en.wikipedia.org/wiki/Human_weight weights] and [http://en.wikipedia.org/wiki/Human_height heights] are known to be approximately Normally distributed. Look at the [[SOCR_Data_Dinov_020108_HeightsWeights |SOCR Weighs and Heights Dataset and use the [[SOCR_EduMaterials_Activities_Histogram_Graphs | SOCR Charts]] to validate these statements based on this sample dataset. | |
| - | + | ||
| - | + | * Suppose the heights of college women are approximately Normally distributed with a mean of 65 inches and a standard deviation of 2 inches. If a randomly chosen college woman is at the 10<sup>th</sup> percentile (shortest 10% for women) in height for college women, then what is the largest height closest to hers? | |
| - | | | + | <center>[[Image:SOCR_EBook_Dinov_RV_Normal_013108_Fig14.jpg|500px]]</center> |
<hr> | <hr> | ||
Revision as of 00:00, 2 February 2008
Contents |
General Advance-Placement (AP) Statistics Curriculum - Nonstandard Normal Distribution & Experiments: Finding Critical Values
Nonstandard Normal Distribution & Experiments: Finding Scores (Critical Values)
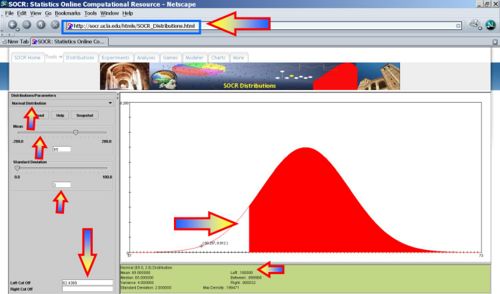
In addition to being able to compute probability (p) values, we often need to estimate the critical values of the Normal distribution for a given p-value.
- The back and forth linear transformations converting between Standard and General Normal distributions are alwasy useful in such analyses (Let X denotes General (
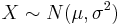 ) and Z denotes Standard (
) and Z denotes Standard (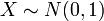 ) Normal random variables):
) Normal random variables):
-
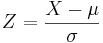 converts general normal scores to standard (Z) values.
converts general normal scores to standard (Z) values.
- X = μ + Zσ converts standard scores to general normal values.
Examples
This Distributions help-page may be useful in understanding SOCR Distribution Applet.
Textbook prices
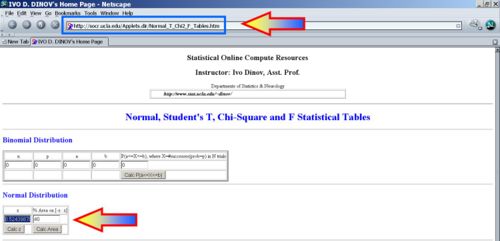
Suppose the amount of money college students spend each semester on textbooks is normally distributed with a mean of $195 and a standard deviation of $20. If we ask a random college students from this population how much he spent on books this semester, what is the maximum dollar amount that would guagantee she spends only as much as 30% of the population? (P(X < 184.512) = 0.3)
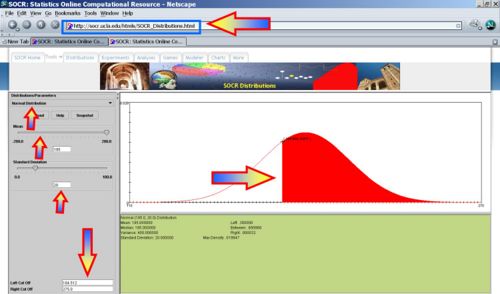
You can also do this problem exactly using the SOCR high-precision Nornal Distribution Calculator. If zo = − 0.5243987892920383, then P( − zo < Z < zo) = 0.4 and P(Z<z_o)=0.3. Thus, xo = μ + zoσ = 195 + ( − 0.5243987892920383) * 20 = 184.512024214159234.
Human Weights and Heights
Human weights and heights are known to be approximately Normally distributed. Look at the [[SOCR_Data_Dinov_020108_HeightsWeights |SOCR Weighs and Heights Dataset and use the SOCR Charts to validate these statements based on this sample dataset.
- Suppose the heights of college women are approximately Normally distributed with a mean of 65 inches and a standard deviation of 2 inches. If a randomly chosen college woman is at the 10th percentile (shortest 10% for women) in height for college women, then what is the largest height closest to hers?
References
- Histogram plots
- Box-and-whisker plots
- Dotplot
- Quantile-Quantile probability plot
- SOCR High-Precision Normal Distribution Calculator
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:
