AP Statistics Curriculum 2007 Normal Critical
From Socr
(→Human Weights and Heights) |
|||
| Line 19: | Line 19: | ||
====Human Weights and Heights==== | ====Human Weights and Heights==== | ||
| - | Human [http://en.wikipedia.org/wiki/Human_weight weights] and [http://en.wikipedia.org/wiki/Human_height heights] are known to be approximately Normally distributed. Look at the [[SOCR_Data_Dinov_020108_HeightsWeights |SOCR Weighs and Heights Dataset and use the [[SOCR_EduMaterials_Activities_Histogram_Graphs | SOCR Charts]] to validate these statements based on this sample dataset. | + | Human [http://en.wikipedia.org/wiki/Human_weight weights] and [http://en.wikipedia.org/wiki/Human_height heights] are known to be approximately Normally distributed. Look at the [[SOCR_Data_Dinov_020108_HeightsWeights |SOCR Weighs and Heights Dataset]] and use the [[SOCR_EduMaterials_Activities_Histogram_Graphs | SOCR Charts]] to validate these statements based on this sample dataset. |
* Suppose the heights of college women are approximately Normally distributed with a mean of 65 inches and a standard deviation of 2 inches. If a randomly chosen college woman is at the 10<sup>th</sup> percentile (shortest 10% for women) in height for college women, then what is the largest height closest to hers? | * Suppose the heights of college women are approximately Normally distributed with a mean of 65 inches and a standard deviation of 2 inches. If a randomly chosen college woman is at the 10<sup>th</sup> percentile (shortest 10% for women) in height for college women, then what is the largest height closest to hers? | ||
Revision as of 00:01, 2 February 2008
Contents |
General Advance-Placement (AP) Statistics Curriculum - Nonstandard Normal Distribution & Experiments: Finding Critical Values
Nonstandard Normal Distribution & Experiments: Finding Scores (Critical Values)
In addition to being able to compute probability (p) values, we often need to estimate the critical values of the Normal distribution for a given p-value.
- The back and forth linear transformations converting between Standard and General Normal distributions are alwasy useful in such analyses (Let X denotes General (
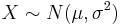 ) and Z denotes Standard (
) and Z denotes Standard (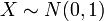 ) Normal random variables):
) Normal random variables):
-
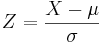 converts general normal scores to standard (Z) values.
converts general normal scores to standard (Z) values.
- X = μ + Zσ converts standard scores to general normal values.
Examples
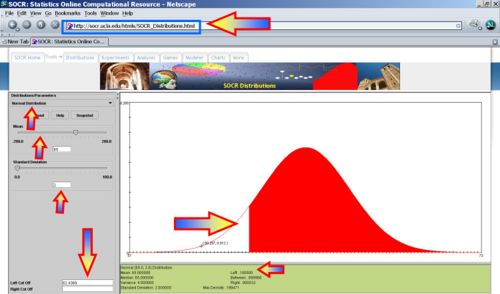
This Distributions help-page may be useful in understanding SOCR Distribution Applet.
Textbook prices
Suppose the amount of money college students spend each semester on textbooks is normally distributed with a mean of $195 and a standard deviation of $20. If we ask a random college students from this population how much he spent on books this semester, what is the maximum dollar amount that would guagantee she spends only as much as 30% of the population? (P(X < 184.512) = 0.3)
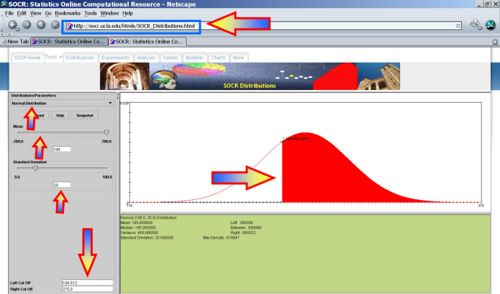
You can also do this problem exactly using the SOCR high-precision Nornal Distribution Calculator. If zo = − 0.5243987892920383, then P( − zo < Z < zo) = 0.4 and P(Z<z_o)=0.3. Thus, xo = μ + zoσ = 195 + ( − 0.5243987892920383) * 20 = 184.512024214159234.
Human Weights and Heights
Human weights and heights are known to be approximately Normally distributed. Look at the SOCR Weighs and Heights Dataset and use the SOCR Charts to validate these statements based on this sample dataset.
- Suppose the heights of college women are approximately Normally distributed with a mean of 65 inches and a standard deviation of 2 inches. If a randomly chosen college woman is at the 10th percentile (shortest 10% for women) in height for college women, then what is the largest height closest to hers?
References
- Histogram plots
- Box-and-whisker plots
- Dotplot
- Quantile-Quantile probability plot
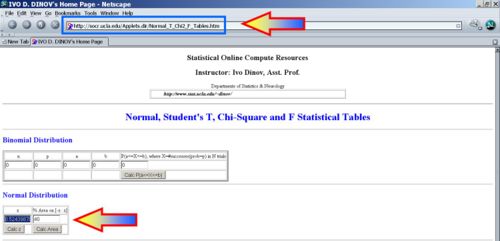
- SOCR High-Precision Normal Distribution Calculator
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:
