AP Statistics Curriculum 2007 Normal Prob
From Socr
m (→Assessing Normality) |
|||
| (30 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
| - | ==[[AP_Statistics_Curriculum_2007 | General Advance-Placement (AP) Statistics Curriculum]] - | + | ==[[AP_Statistics_Curriculum_2007 | General Advance-Placement (AP) Statistics Curriculum]] - Non-Standard Normal Distribution and Experiments: Finding Probabilities== |
| + | |||
| + | Due to the [[AP_Statistics_Curriculum_2007_Limits_CLT |Central Limit Theorem]], the Normal Distribution is perhaps the most important model for studying various quantitative phenomena. Many numerical measurements (e.g., weight, time, etc.) can be well approximated by the normal distribution. While the mechanisms underlying natural processes may often be unknown, the use of the normal model can be theoretically justified by assuming that many small, independent effects are additively contributing to each observation. | ||
=== General Normal Distribution=== | === General Normal Distribution=== | ||
| - | The | + | The (general) Normal Distribution, <math>N(\mu, \sigma^2)</math>, where <math>\mu</math> is the mean and <math>\sigma^2</math> is the variance, is a continuous distribution that has similar exact ''areas'' in terms of symmetric intervals around the origin on x-axis, relative to its mean and variance, as the [[AP_Statistics_Curriculum_2007_Normal_Std |Standard Normal Distribution]]: |
| - | * The area: - | + | * The area: <math>\mu -\sigma < x < \mu+\sigma = 0.8413 - 0.1587 = 0.6826</math> |
| - | * The area: -2 | + | * The area: <math>\mu -2\sigma < x < \mu+2\sigma = 0.9772 - 0.0228 = 0.9544</math> |
| - | * The area: -3 | + | * The area: <math>\mu -3\sigma < x < \mu +3\sigma= 0.9987 - 0.0013 = 0.9974</math> |
| - | <center>[[Image: | + | * Note that the [http://en.wikipedia.org/wiki/Inflection_point inflection points] (<math>f ''(x)=0</math>) of the (general) Normal density function are <math>\pm \sigma</math>. |
| + | <center>[[Image:SOCR_EBook_Dinov_RV_Normal_013108_Fig6.jpg|500px]]</center> | ||
| - | * | + | * General Normal ''density'' function <math>f(x)= {e^{{-(x-\mu)^2} \over 2\sigma^2} \over \sqrt{2 \pi\sigma^2}}.</math> |
| + | * General Normal ''cumulative distribution'' function <math>\Phi(y)= \int_{-\infty}^{y}{{e^{{-(x-\mu)^2} \over 2\sigma^2} \over \sqrt{2 \pi\sigma^2}} dx}.</math> | ||
| - | |||
| - | === | + | * See the special case of [[AP_Statistics_Curriculum_2007#The_Standard_Normal_Distribution | Standard Normal Distribution]] where the mean is set to zero and a variance to one. |
| - | + | ||
| - | * | + | * The relation between the Standard and the General Normal Distribution is provided by these simple linear transformations (Suppose ''X'' denotes General and ''Z'' denotes Standard Normal Random Variables): |
| - | <center>[[Image: | + | : <math>Z = {X-\mu \over \sigma}</math> converts general normal scores to standard (Z) values. |
| - | * | + | : <math>X = \mu +Z\times\sigma</math> converts standard scores to general normal values. |
| - | <center>[[Image: | + | |
| - | * | + | ===Examples=== |
| - | <center>[[Image: | + | |
| - | * | + | ====[[SOCR_EduMaterials_Activities_Normal_Probability_examples | A large number of Normal distribution examples using SOCR tools]]==== |
| - | <center>[[Image: | + | |
| - | * | + | ====Sums and averages of independent Normal random variables==== |
| - | <center>[[Image: | + | |
| + | * Let X1, X2, and X3 represent the heights of 3 random individuals. Suppose the heights are Normally distributed with mean 170cm and standard deviation 20 cm (i.e., X1, X2, X3 ~<math>N(\mu=170, \sigma=20)</math>. ''What is the probability that the total sum T=X1+X2+X3 is less than 500cm? That is, find P(T<500)''. As the [[AP_Statistics_Curriculum_2007_Limits_CLT|X variables are Normal and independent, the total sum, T, will be Normal]](<math>\mu_T, \sigma_T</math>) and we need to find the parameters <math>\mu_T, \sigma_T</math>. | ||
| + | ** <math>\mu_T=E(T)=E(X1+X2+X3) = E(X1)+E(X2)+E(X3)=3\times 170=510.</math> | ||
| + | ** <math>\sigma_T^2 = Var(T) = Var(X1+X2+X3)=Var(X1)+Var(X2)+Var(X3)=</math><math>20^2+20^2+20^2=1,200</math>, and <math>\sigma_T=\sqrt{1,200}=34.64.</math> | ||
| + | ** Thus, T~<math>N(\mu_T=510,\sigma_T=34.64)</math>, and P(T<500)= 0.386380, which can be computed using the [http://socr.ucla.edu/htmls/dist/Normal_Distribution.html SOCR Normal Distribution Calculator] or the [http://socr.ucla.edu/Applets.dir/Z-table.html SOCR Standard Normal Z Table] via the standardizing transformation. | ||
| + | |||
| + | * If A is the average of the 3 heights, A=(X1+X2+X3)/3, ''what is the central 50-th percentile for the variable A''? That is, what are the lower (a1) and upper (a2) bounds that give P(a1<A<a2)=0.5, where a1 and a2 are symmetric with respect to the expected value of A, <math>E(A)=\mu=170</math>)? | ||
| + | ** Note that it suffices to find one of the bounds (say a2) as these bounds are symmetric around the mean, 170. Thus, we are looking for a2, such that P(170<A<a2)=0.25, which is also the same as P(a1<A<170)=0.25. | ||
| + | ** The [[AP_Statistics_Curriculum_2007_Limits_CLT|distribution of the average]] A~<math>N(\mu=170, \sigma)</math>. | ||
| + | ** <math>Var(A) = Var((1/3)(X1+X2+X3))=(1/9)(Var(X1)+Var(X2)+Var(X3))=(1/9)(20^2+20^2+20^2)=133.33</math>, and <math>\sigma = 11.55</math>. Thus, A~<math>N(\mu=170, \sigma=11.55)</math>. | ||
| + | ** As before, we can the [http://socr.ucla.edu/htmls/dist/Normal_Distribution.html SOCR Normal Distribution Calculator] or the [http://socr.ucla.edu/Applets.dir/Z-table.html SOCR Standard Normal Z Table] via the standardizing transformation to compute a2=177.8, and <math>a1=\mu -(a2-\mu)=162.2</math>, as P(162.2<A<170)=P(170<A<177.8)=0.25. | ||
| + | ** Therefore, the central 50-th percentile for the average height is [162.2 : 177.8]. | ||
| + | |||
| + | ====Systolic Arterial Pressure Example==== | ||
| + | This [[Help_pages_for_SOCR_Distributions | Distributions help-page may be useful in understanding SOCR Distribution Applet]]. | ||
| + | |||
| + | Suppose that the average systolic blood pressure (SBP) for a Los Angeles freeway commuter follows a Normal distribution with mean 130 mmHg and standard deviation 20 mmHg. Denote ''X'' to be the random variable representing the SBP measure for a randomly chosen commuter. Then <math>X\sim N(\mu=130, \sigma^2 =20^2)</math>. | ||
| + | |||
| + | * Find the percentage of LA freeway commuters that have a SBP less than 100. That is compute the following probability: ''p=P(X<100)=?'' (p=0.066776) | ||
| + | <center>[[Image:SOCR_EBook_Dinov_RV_Normal_013108_Fig7.jpg|500px]]</center> | ||
| + | |||
| + | * If ''normal SBP'' is defined by the range [110 ; 140], and we take a random sample of 1,000 commuters and measure their SBP, how many would be expected to have ''normal SBP''? (Number = 1,000P(110<X<140)= 1,000*0.532807=532.807). | ||
| + | <center>[[Image:SOCR_EBook_Dinov_RV_Normal_013108_Fig8.jpg|500px]]</center> | ||
| + | |||
| + | * What is the 90<sup>th</sup> percentile for the SBP? That is what is <math>x_o</math>, so that <math>P(X<x_o)=0.9</math>? | ||
| + | <center>[[Image:SOCR_EBook_Dinov_RV_Normal_013108_Fig9.jpg|500px]]</center> | ||
| + | |||
| + | * What is the range of SBP values that contain the central 80% of the SBPs for all commuters? That is what are <math>x_o, x_1</math>, so that <math>P(x_0<X<x_1)=0.8</math> and <math>{x_o+x_1\over2}=\mu=130</math> (i.e., they are symmetric around the mean)? (<math>x_o=104, x_1=156</math>) | ||
| + | <center>[[Image:SOCR_EBook_Dinov_RV_Normal_013108_Fig10.jpg|500px]]</center> | ||
| + | |||
| + | ===Assessing Normality=== | ||
| + | How can we tell if data collected from a process or experiment we observe is normally distributed? There are several methods for ''checking normality'': | ||
| + | * Symmetry: Are the [[AP_Statistics_Curriculum_2007_EDA_Center |mean and median]] of the dataset equal (Mean = Median)? Use the [[AP_Statistics_Curriculum_2007_Distrib_MeanVar#Notable_Moments | skewness measure]]. | ||
| + | * Flatness: Is the data distribution as flat as the Normal distribution? Use the [[AP_Statistics_Curriculum_2007_Distrib_MeanVar#Notable_Moments |kurtosis measure]]. | ||
| + | * Check the data [[SOCR_EduMaterials_Activities_Histogram_Graphs | histogram]], [[SOCR_EduMaterials_Activities_BoxPlot | box-and-whisker]] and [[SOCR_EduMaterials_Activities_DotChart |dotplot]] for bias (skewness), asymmetry, outliers, etc. | ||
| + | * Empirical Rule - check the percent of data that falls within 1, 2 and 3 [[AP_Statistics_Curriculum_2007_EDA_Var | SD]]s from the mean (should be approximately 68%, 95% and 99.7%). | ||
| + | * Or we can do a [[SOCR_EduMaterials_Activities_QQChart |Quantile-Quantile Probability plot]] comparing the quantiles of the data against their Normal distribution counterparts. | ||
| + | <center>[[Image:SOCR_EBook_Dinov_RV_Normal_013108_Fig11.jpg|500px]]</center> | ||
| + | |||
| + | * ''Why do we care if the data is normally distributed? Having evidence that the data we are analyzing is normally distributed allows us to use the (General) Normal distribution as a model to calculate the probabilities of various events and assess significant observations.'' | ||
| + | |||
| + | * Example: Suppose we are given the heights for 11 women. | ||
| + | ** First we need to show that there is no evidence suggesting that the Normal and Data distributions are significantly distinct. | ||
| + | ** Then, we want to use the normal distribution to make inference on women heights. If the height of a randomly chosen woman is measured, how likely is that she'll be taller than 60 inches? 70 inches? Between 55 and 65 inches? | ||
| + | <center> | ||
| + | {| class="wikitable" style="text-align:center; width:75%" border="1" | ||
| + | |- | ||
| + | | Height (in.) || 61.0 || 62.5 || 63.0 || 64.0 || 64.5 || 65.0 || 66.5 || 67.0 || 68.0 || 68.5 || 70.5 | ||
| + | |}</center> | ||
| + | |||
| + | * [http://en.wikipedia.org/wiki/Standard_normal_distribution#Normality_tests There are also a number of quantitative methods (statistical tests) to assess normality]. | ||
| + | |||
| + | ===[[EBook_Problems_Normal_Prob|Problems]]=== | ||
<hr> | <hr> | ||
| + | |||
===References=== | ===References=== | ||
| + | * [[SOCR_EduMaterials_Activities_Histogram_Graphs | Histogram Plots]] | ||
| + | * [[SOCR_EduMaterials_Activities_BoxPlot | Box-and-Whisker Plots]] | ||
| + | * [[SOCR_EduMaterials_Activities_DotChart |Dotplot]] | ||
| + | * [[SOCR_EduMaterials_Activities_QQChart |Quantile-Quantile Probability Plot]] | ||
<hr> | <hr> | ||
Current revision as of 15:48, 3 May 2013
Contents |
General Advance-Placement (AP) Statistics Curriculum - Non-Standard Normal Distribution and Experiments: Finding Probabilities
Due to the Central Limit Theorem, the Normal Distribution is perhaps the most important model for studying various quantitative phenomena. Many numerical measurements (e.g., weight, time, etc.) can be well approximated by the normal distribution. While the mechanisms underlying natural processes may often be unknown, the use of the normal model can be theoretically justified by assuming that many small, independent effects are additively contributing to each observation.
General Normal Distribution
The (general) Normal Distribution, N(μ,σ2), where μ is the mean and σ2 is the variance, is a continuous distribution that has similar exact areas in terms of symmetric intervals around the origin on x-axis, relative to its mean and variance, as the Standard Normal Distribution:
- The area: μ − σ < x < μ + σ = 0.8413 − 0.1587 = 0.6826
- The area: μ − 2σ < x < μ + 2σ = 0.9772 − 0.0228 = 0.9544
- The area: μ − 3σ < x < μ + 3σ = 0.9987 − 0.0013 = 0.9974
- Note that the inflection points (f''(x) = 0) of the (general) Normal density function are
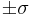 .
.

- General Normal density function
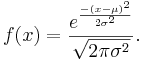
- General Normal cumulative distribution function
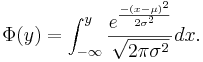
- See the special case of Standard Normal Distribution where the mean is set to zero and a variance to one.
- The relation between the Standard and the General Normal Distribution is provided by these simple linear transformations (Suppose X denotes General and Z denotes Standard Normal Random Variables):
-
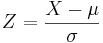 converts general normal scores to standard (Z) values.
converts general normal scores to standard (Z) values.
-
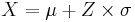 converts standard scores to general normal values.
converts standard scores to general normal values.
Examples
A large number of Normal distribution examples using SOCR tools
Sums and averages of independent Normal random variables
- Let X1, X2, and X3 represent the heights of 3 random individuals. Suppose the heights are Normally distributed with mean 170cm and standard deviation 20 cm (i.e., X1, X2, X3 ~N(μ = 170,σ = 20). What is the probability that the total sum T=X1+X2+X3 is less than 500cm? That is, find P(T<500). As the X variables are Normal and independent, the total sum, T, will be Normal(μT,σT) and we need to find the parameters μT,σT.
-
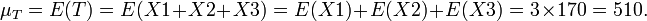
-
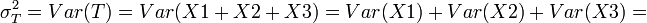 202 + 202 + 202 = 1,200, and
202 + 202 + 202 = 1,200, and 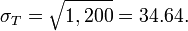
- Thus, T~N(μT = 510,σT = 34.64), and P(T<500)= 0.386380, which can be computed using the SOCR Normal Distribution Calculator or the SOCR Standard Normal Z Table via the standardizing transformation.
-
- If A is the average of the 3 heights, A=(X1+X2+X3)/3, what is the central 50-th percentile for the variable A? That is, what are the lower (a1) and upper (a2) bounds that give P(a1<A<a2)=0.5, where a1 and a2 are symmetric with respect to the expected value of A, E(A) = μ = 170)?
- Note that it suffices to find one of the bounds (say a2) as these bounds are symmetric around the mean, 170. Thus, we are looking for a2, such that P(170<A<a2)=0.25, which is also the same as P(a1<A<170)=0.25.
- The distribution of the average A~N(μ = 170,σ).
- Var(A) = Var((1 / 3)(X1 + X2 + X3)) = (1 / 9)(Var(X1) + Var(X2) + Var(X3)) = (1 / 9)(202 + 202 + 202) = 133.33, and σ = 11.55. Thus, A~N(μ = 170,σ = 11.55).
- As before, we can the SOCR Normal Distribution Calculator or the SOCR Standard Normal Z Table via the standardizing transformation to compute a2=177.8, and a1 = μ − (a2 − μ) = 162.2, as P(162.2<A<170)=P(170<A<177.8)=0.25.
- Therefore, the central 50-th percentile for the average height is [162.2 : 177.8].
Systolic Arterial Pressure Example
This Distributions help-page may be useful in understanding SOCR Distribution Applet.
Suppose that the average systolic blood pressure (SBP) for a Los Angeles freeway commuter follows a Normal distribution with mean 130 mmHg and standard deviation 20 mmHg. Denote X to be the random variable representing the SBP measure for a randomly chosen commuter. Then 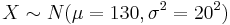 .
.
- Find the percentage of LA freeway commuters that have a SBP less than 100. That is compute the following probability: p=P(X<100)=? (p=0.066776)
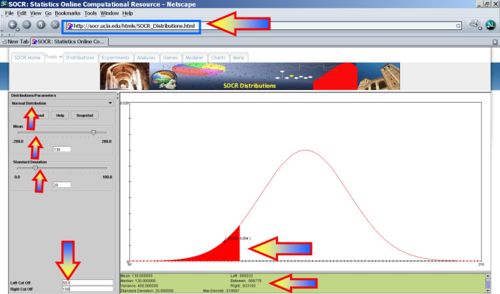
- If normal SBP is defined by the range [110 ; 140], and we take a random sample of 1,000 commuters and measure their SBP, how many would be expected to have normal SBP? (Number = 1,000P(110<X<140)= 1,000*0.532807=532.807).
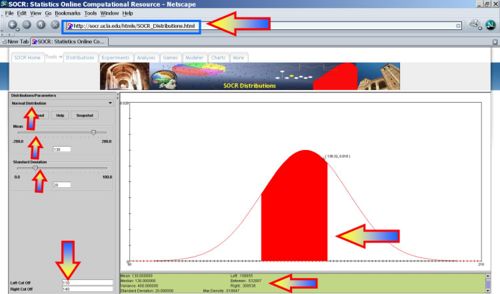
- What is the 90th percentile for the SBP? That is what is xo, so that P(X < xo) = 0.9?
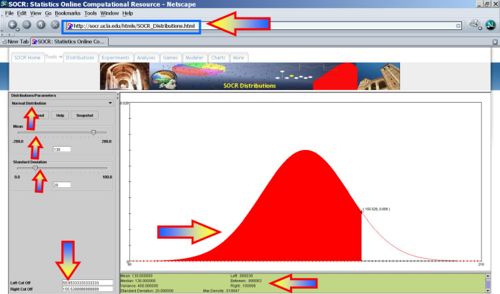
- What is the range of SBP values that contain the central 80% of the SBPs for all commuters? That is what are xo,x1, so that P(x0 < X < x1) = 0.8 and
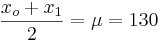 (i.e., they are symmetric around the mean)? (xo = 104,x1 = 156)
(i.e., they are symmetric around the mean)? (xo = 104,x1 = 156)
Assessing Normality
How can we tell if data collected from a process or experiment we observe is normally distributed? There are several methods for checking normality:
- Symmetry: Are the mean and median of the dataset equal (Mean = Median)? Use the skewness measure.
- Flatness: Is the data distribution as flat as the Normal distribution? Use the kurtosis measure.
- Check the data histogram, box-and-whisker and dotplot for bias (skewness), asymmetry, outliers, etc.
- Empirical Rule - check the percent of data that falls within 1, 2 and 3 SDs from the mean (should be approximately 68%, 95% and 99.7%).
- Or we can do a Quantile-Quantile Probability plot comparing the quantiles of the data against their Normal distribution counterparts.
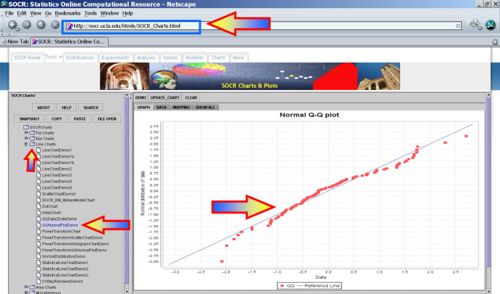
- Why do we care if the data is normally distributed? Having evidence that the data we are analyzing is normally distributed allows us to use the (General) Normal distribution as a model to calculate the probabilities of various events and assess significant observations.
- Example: Suppose we are given the heights for 11 women.
- First we need to show that there is no evidence suggesting that the Normal and Data distributions are significantly distinct.
- Then, we want to use the normal distribution to make inference on women heights. If the height of a randomly chosen woman is measured, how likely is that she'll be taller than 60 inches? 70 inches? Between 55 and 65 inches?
| Height (in.) | 61.0 | 62.5 | 63.0 | 64.0 | 64.5 | 65.0 | 66.5 | 67.0 | 68.0 | 68.5 | 70.5 |
Problems
References
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:
