AP Statistics Curriculum 2007 Normal Prob
From Socr
| Line 1: | Line 1: | ||
==[[AP_Statistics_Curriculum_2007 | General Advance-Placement (AP) Statistics Curriculum]] - Nonstandard Normal Distribution & Experiments: Finding Probabilities== | ==[[AP_Statistics_Curriculum_2007 | General Advance-Placement (AP) Statistics Curriculum]] - Nonstandard Normal Distribution & Experiments: Finding Probabilities== | ||
| - | === | + | === General Normal Distribution=== |
| - | + | The standard normal distribution is a continuous distribution where the following exact ''areas'' are bound between the Standard Normal Density function and the x-axis on the symmetric intervals around the origin: | |
| - | <center>[[Image: | + | * The area: -1 < z < 1 = 0.8413 - 0.1587 = 0.6826 |
| + | * The area: -2.0 < z < 2.0 = 0.9772 - 0.0228 = 0.9544 | ||
| + | * The area: -3.0 < z < 3.0 = 0.9987 - 0.0013 = 0.9974 | ||
| + | <center>[[Image:SOCR_EBook_Dinov_RV_Normal_013108_Fig0.jpg|500px]]</center> | ||
| - | = | + | * Standard Normal density function <math>f(x)= {e^{-x^2} \over \sqrt{2 \pi}}.</math> |
| - | + | ||
| - | * | + | * The Standard Normal distribution is also a special case of the [[AP_Statistics_Curriculum_2007_Normal_Prob | more general normal distribution]] where the mean is set to zero and a variance to one. The Standard Normal distribution is often called the ''bell curve'' because the graph of its probability density resembles a bell. |
| - | === | + | ===Experiments=== |
| - | + | Suppose we decide to test the state of 100 used batteries. To do that, we connect each battery to a volt-meter by randomly attaching the positive (+) and negative (-) battery terminals to the corresponding volt-meter's connections. Electrical current always flows from + to -, i.e., the current goes in the direction of the voltage drop. Depending upon which way the battery is connected to the volt-meter we can observe positive or negative voltage recordings (voltage is just a difference, which forces current to flow from higher to the lower voltage.) Denote <math>X_i</math>={measured voltage for battery i} - this is random variable 0 and assume the distribution of all <math>X_i</math> is Standard Normal, <math>X_i \sim N(0,1)</math>. Use the Normal Distribution (with mean=0 and variance=1) in the [http://socr.ucla.edu/htmls/SOCR_Distributions.html SOCR Distribution applet] to address the following questions. This [[Help_pages_for_SOCR_Distributions | Distributions help-page may be useful in understanding SOCR Distribution Applet]]. How many batteries, from the sample of 100, can we expect to have? | |
| - | + | * Absolute Voltage > 1? P(X>1) = 0.1586, thus we expect 15-16 batteries to have voltage exceeding 1. | |
| - | + | <center>[[Image:SOCR_EBook_Dinov_RV_Normal_013108_Fig1.jpg|500px]]</center> | |
| - | + | * |Absolute Voltage| > 1? P(|X|>1) = 1- 0.682689=0.3173, thus we expect 31-32 batteries to have absolute voltage exceeding 1. | |
| - | == | + | <center>[[Image:SOCR_EBook_Dinov_RV_Normal_013108_Fig2.jpg|500px]]</center> |
| - | * | + | * Voltage < -2? P(X<-2) = 0.0227, thus we expect 2-3 batteries to have voltage less than -2. |
| - | + | <center>[[Image:SOCR_EBook_Dinov_RV_Normal_013108_Fig3.jpg|500px]]</center> | |
| - | == | + | * Voltage <= -2? P(X<=-2) = 0.0227, thus we expect 2-3 batteries to have voltage less than or equal to -2. |
| - | + | <center>[[Image:SOCR_EBook_Dinov_RV_Normal_013108_Fig3.jpg|500px]]</center> | |
| - | + | * -1.7537 < Voltage < 0.8465? P(-1.7537 < X < 0.8465) = 0.761622, thus we expect 76 batteries to have voltage in this range. | |
| - | * | + | <center>[[Image:SOCR_EBook_Dinov_RV_Normal_013108_Fig4.jpg|500px]]</center> |
| - | + | ||
| - | == | + | |
| - | + | ||
| - | + | ||
| - | * | + | |
<hr> | <hr> | ||
===References=== | ===References=== | ||
| - | |||
<hr> | <hr> | ||
Revision as of 20:19, 31 January 2008
Contents |
General Advance-Placement (AP) Statistics Curriculum - Nonstandard Normal Distribution & Experiments: Finding Probabilities
General Normal Distribution
The standard normal distribution is a continuous distribution where the following exact areas are bound between the Standard Normal Density function and the x-axis on the symmetric intervals around the origin:
- The area: -1 < z < 1 = 0.8413 - 0.1587 = 0.6826
- The area: -2.0 < z < 2.0 = 0.9772 - 0.0228 = 0.9544
- The area: -3.0 < z < 3.0 = 0.9987 - 0.0013 = 0.9974

- Standard Normal density function
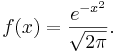
- The Standard Normal distribution is also a special case of the more general normal distribution where the mean is set to zero and a variance to one. The Standard Normal distribution is often called the bell curve because the graph of its probability density resembles a bell.
Experiments
Suppose we decide to test the state of 100 used batteries. To do that, we connect each battery to a volt-meter by randomly attaching the positive (+) and negative (-) battery terminals to the corresponding volt-meter's connections. Electrical current always flows from + to -, i.e., the current goes in the direction of the voltage drop. Depending upon which way the battery is connected to the volt-meter we can observe positive or negative voltage recordings (voltage is just a difference, which forces current to flow from higher to the lower voltage.) Denote Xi={measured voltage for battery i} - this is random variable 0 and assume the distribution of all Xi is Standard Normal, 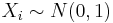 . Use the Normal Distribution (with mean=0 and variance=1) in the SOCR Distribution applet to address the following questions. This Distributions help-page may be useful in understanding SOCR Distribution Applet. How many batteries, from the sample of 100, can we expect to have?
. Use the Normal Distribution (with mean=0 and variance=1) in the SOCR Distribution applet to address the following questions. This Distributions help-page may be useful in understanding SOCR Distribution Applet. How many batteries, from the sample of 100, can we expect to have?
- Absolute Voltage > 1? P(X>1) = 0.1586, thus we expect 15-16 batteries to have voltage exceeding 1.
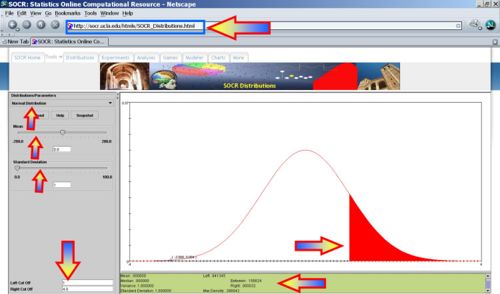
- |Absolute Voltage| > 1? P(|X|>1) = 1- 0.682689=0.3173, thus we expect 31-32 batteries to have absolute voltage exceeding 1.
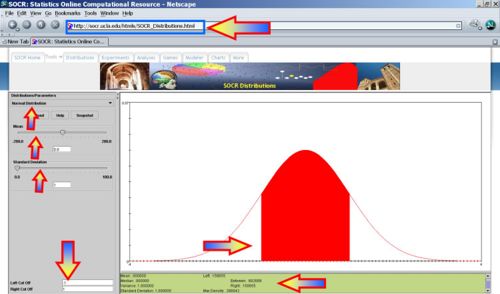
- Voltage < -2? P(X<-2) = 0.0227, thus we expect 2-3 batteries to have voltage less than -2.
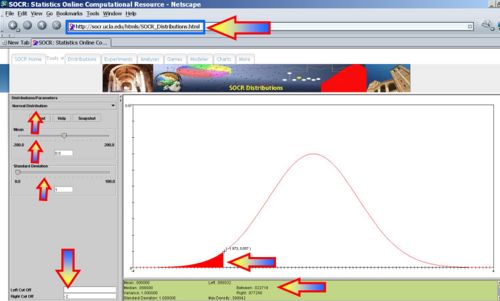
- Voltage <= -2? P(X<=-2) = 0.0227, thus we expect 2-3 batteries to have voltage less than or equal to -2.

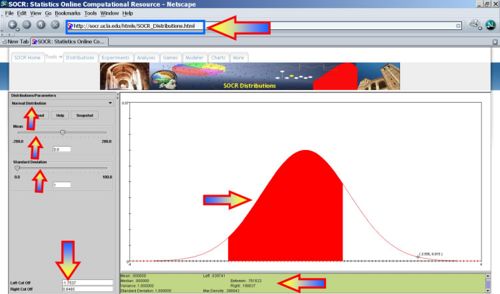
- -1.7537 < Voltage < 0.8465? P(-1.7537 < X < 0.8465) = 0.761622, thus we expect 76 batteries to have voltage in this range.
References
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:
