AP Statistics Curriculum 2007 Normal Prob
From Socr
Contents |
General Advance-Placement (AP) Statistics Curriculum - Nonstandard Normal Distribution & Experiments: Finding Probabilities
Due to the Central Limit Theorem, the normal distribution is perhaps the most important model for studying various quantitative phenomena. Many numerical measurements (e.g., weight, time, etc.) can be well approximated by the normal distribution. While the mechanisms underlying natural processes may often be unknown, the use of the normal model can be theoretically justified by assuming that many small, independent effects are additively contributing to each observation.
General Normal Distribution
The (general) normal distribution is a continuous distribution that has similar exact areas, bound in terms of its mean, like the Standard Normal distribution and the x-axis on the symmetric intervals around the origin:
- The area: μ − σ < x < μ + σ = 0.8413 − 0.1587 = 0.6826
- The area: μ − 2σ < x < μ + 2σ = 0.9772 − 0.0228 = 0.9544
- The area: μ − 3σ < x < μ + 3σ = 0.9987 − 0.0013 = 0.9974

- General Normal density function
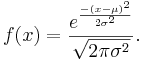
- See the special case of Standard Normal distribution where the mean is set to zero and a variance to one.
- The relation between the Standard and the General Normal distribution is provided by these simple linear transformations (Supposed X denotes General and Z denotes Standard Normal random variables):
-
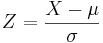 converts general normal scores to standard (Z) values.
converts general normal scores to standard (Z) values.
- X = μ + Zσ converts standard scores to general normal values.
Experiments
TBD
This Distributions help-page may be useful in understanding SOCR Distribution Applet. How many batteries, from the sample of 100, can we expect to have?
- Absolute Voltage > 1? P(X>1) = 0.1586, thus we expect 15-16 batteries to have voltage exceeding 1.
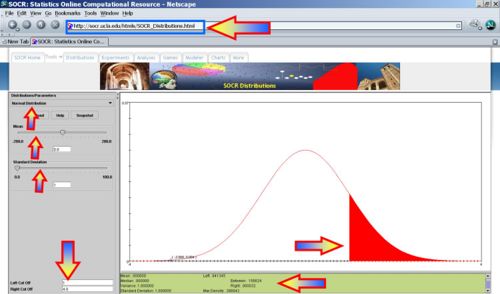
- |Absolute Voltage| > 1? P(|X|>1) = 1- 0.682689=0.3173, thus we expect 31-32 batteries to have absolute voltage exceeding 1.
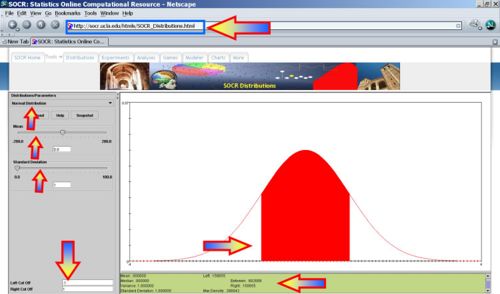
- Voltage < -2? P(X<-2) = 0.0227, thus we expect 2-3 batteries to have voltage less than -2.
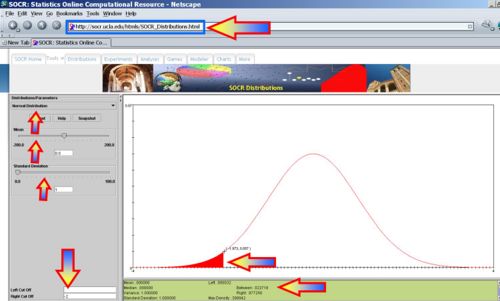
- Voltage <= -2? P(X<=-2) = 0.0227, thus we expect 2-3 batteries to have voltage less than or equal to -2.

- -1.7537 < Voltage < 0.8465? P(-1.7537 < X < 0.8465) = 0.761622, thus we expect 76 batteries to have voltage in this range.
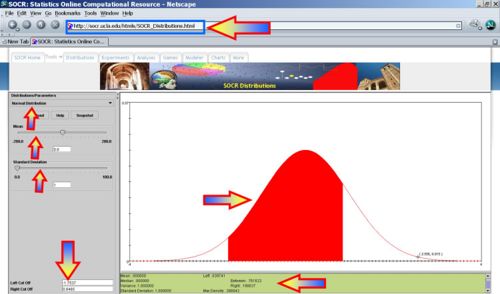
References
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:
