AP Statistics Curriculum 2007 Normal Std
From Socr
(→Appendix) |
m (→Standard Normal Distribution) |
||
| (8 intermediate revisions not shown) | |||
| Line 5: | Line 5: | ||
* Standard Normal ''density'' function <math>f(x)= {e^{-x^2 \over 2} \over \sqrt{2 \pi}}.</math> | * Standard Normal ''density'' function <math>f(x)= {e^{-x^2 \over 2} \over \sqrt{2 \pi}}.</math> | ||
* Standard Normal ''cumulative distribution'' function <math>\Phi(y)= \int_{-\infty}^{y}{{e^{-x^2 \over 2} \over \sqrt{2 \pi}} dx}.</math> | * Standard Normal ''cumulative distribution'' function <math>\Phi(y)= \int_{-\infty}^{y}{{e^{-x^2 \over 2} \over \sqrt{2 \pi}} dx}.</math> | ||
| - | * Why are these two functions, <math>f(x), \Phi(y)</math> well-defined density and distribution functions, i.e., <math>\int_{-\infty}^{\infty} {f(x)dx}=1</math>? See the appendix below. | + | * Why are these two functions, <math>f(x), \Phi(y)</math> well-defined density and distribution functions, i.e., <math>\int_{-\infty}^{\infty} {f(x)dx}=1</math>? [[AP_Statistics_Curriculum_2007_Normal_Std#Appendix|See the appendix below]]. |
Note that the following exact ''areas'' are bound between the Standard Normal Density Function and the x-axis on these symmetric intervals around the origin: | Note that the following exact ''areas'' are bound between the Standard Normal Density Function and the x-axis on these symmetric intervals around the origin: | ||
| Line 39: | Line 39: | ||
:: <math>x=r\cos(\theta)</math> | :: <math>x=r\cos(\theta)</math> | ||
:: <math>x=r\cos(\theta)</math>, <math>0\le \theta\le 2\pi</math> | :: <math>x=r\cos(\theta)</math>, <math>0\le \theta\le 2\pi</math> | ||
| - | :: Hence, <math>x^2+w^2=r^2</math>, <math>e^{-x^2 \over 2} \times e^{-w^2 \over 2} =e^{-r^2 \over 2}</math>, | + | :: Hence, |
| - | :: <math>dx=\cos(\theta)dr</math> | + | ::: <math>x^2+w^2=r^2</math>, |
| - | :: <math>dy=r\cos(\theta)dr</math> | + | ::: <math>e^{-x^2 \over 2} \times e^{-w^2 \over 2} =e^{-r^2 \over 2}</math>, |
| - | : Therefore, <math>A^2=\int_{0}^{\infty} {\int_{0}^{2\pi} {{e^{-r^2 \over 2} \over 2 \pi} | + | ::: <math>dx=\cos(\theta)dr</math>, and |
| - | : <math>A^2= | + | ::: <math>dy=r\cos(\theta)dr</math>. |
| - | : <math>\int_{0}^{2\pi} {\cos^2(\theta)d\theta}=\int_{0}^{2\pi} {\frac{1+\cos(2\theta)}{2}d\theta}=\pi</math> | + | : Therefore, <math>A^2=\int_{0}^{\infty} {\int_{0}^{2\pi} {{e^{-r^2 \over 2} \over 2 \pi}\cos^2(\theta)rdrd\theta}}</math>, and |
| + | : <math>A^2=\int_{0}^{\infty} {\int_{0}^{2\pi} {{e^{-r^2 \over 2} \over 2 \pi}d{\frac{r^2}{2}}d\theta}}=\int_{0}^{\infty} {{e^{-r^2 \over 2} \over \pi}d{\frac{r^2}{2}}} \times \int_{0}^{2\pi} {\cos^2(\theta)d\theta}=1</math>, since | ||
| + | :: <math>\int_{0}^{2\pi} {\cos^2(\theta)d\theta}=\int_{0}^{2\pi} {\frac{1+\cos(2\theta)}{2}d\theta}=\pi</math>, and | ||
| + | :: <math>\int_{0}^{\infty} {e^{-w}dw}=1</math>. | ||
<hr> | <hr> | ||
Current revision as of 16:28, 8 February 2012
Contents |
General Advance-Placement (AP) Statistics Curriculum - Standard Normal Variables and Experiments
Standard Normal Distribution
The Standard Normal Distribution is a continuous distribution with the following density:
- Standard Normal density function
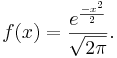
- Standard Normal cumulative distribution function

- Why are these two functions, f(x),Φ(y) well-defined density and distribution functions, i.e.,
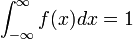 ? See the appendix below.
? See the appendix below.
Note that the following exact areas are bound between the Standard Normal Density Function and the x-axis on these symmetric intervals around the origin:
- The area: -1.0 < x < 1.0 = 0.8413 - 0.1587 = 0.6826
- The area: -2.0 < x < 2.0 = 0.9772 - 0.0228 = 0.9544
- The area: -3.0 < x < 3.0 = 0.9987 - 0.0013 = 0.9974
- Note that the inflection points (f''(x) = 0)of the Standard Normal density function are
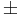 1.
1.

- The Standard Normal distribution is also a special case of the more general normal distribution where the mean is set to zero and the variance is set to one. The Standard Normal distribution is often called the bell curve because the graph of its probability density resembles a bell.
Experiments
Suppose we decide to test the state of 100 used batteries. To do that, we connect each battery to a volt-meter by randomly attaching the positive (+) and negative (-) battery terminals to the corresponding volt-meter's connections. Electrical current always flows from + to -, i.e., the current goes in the direction of the voltage drop. Depending upon which way the battery is connected to the volt-meter we can observe positive or negative voltage recordings (voltage is just a difference, which forces current to flow from higher to the lower voltage.) Denote Xi={measured voltage for battery i} - this is random variable with mean of 0 and unitary variance. Assume the distribution of all Xi is Standard Normal, 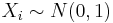 . Use the Normal Distribution (with mean=0 and variance=1) in the SOCR Distribution applet to address the following questions. This Distributions help-page may be useful in understanding SOCR Distribution Applet. How many batteries, from the sample of 100, can we expect to have?
. Use the Normal Distribution (with mean=0 and variance=1) in the SOCR Distribution applet to address the following questions. This Distributions help-page may be useful in understanding SOCR Distribution Applet. How many batteries, from the sample of 100, can we expect to have?
- Absolute Voltage > 1? P(X>1) = 0.1586, thus we expect 15-16 batteries to have voltage exceeding 1.
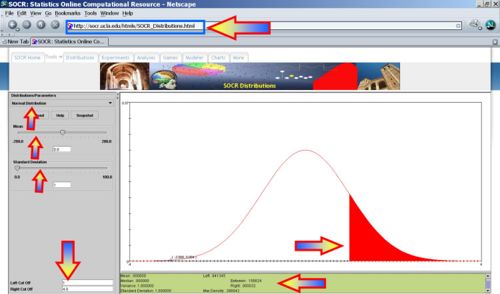
- |Absolute Voltage| > 1? P(|X|>1) = 1- 0.682689=0.3173, thus we expect 31-32 batteries to have absolute voltage exceeding 1.
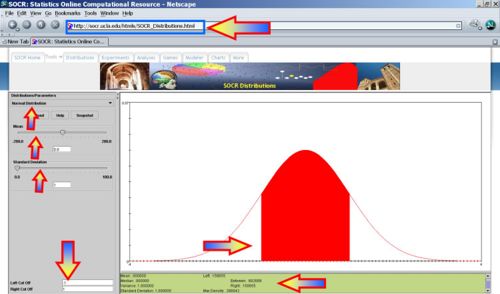
- Voltage < -2? P(X<-2) = 0.0227, thus we expect 2-3 batteries to have voltage less than -2.
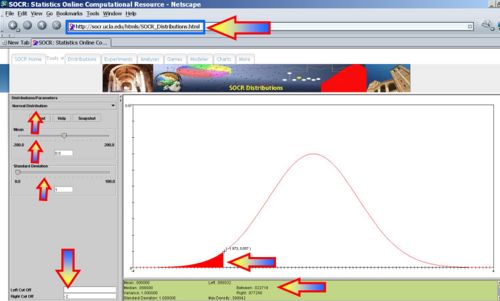
- Voltage <= -2? P(X<=-2) = 0.0227, thus we expect 2-3 batteries to have voltage less than or equal to -2.

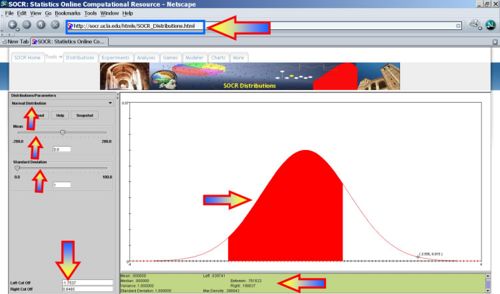
- -1.7537 < Voltage < 0.8465? P(-1.7537 < X < 0.8465) = 0.761622, thus we expect 76 batteries to have voltage in this range.
Problems
Appendix
The derivation below illustrates why the standard normal density function, 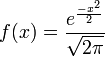 , represents a well-defined density function, i.e.,
, represents a well-defined density function, i.e., 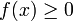 and
and 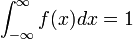 .
.
- Clearly the exponential function
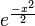 is always non-negative (in fact it's strictly positive for each real value argument).
is always non-negative (in fact it's strictly positive for each real value argument).
- To show that
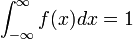 , let
, let 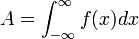 . Then
. Then 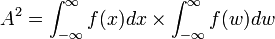 . Thus,
. Thus,
-
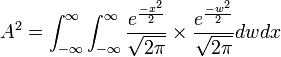 ,
,
- Change variables from Cartesian to polar coordinates:
- x = rcos(θ)
- x = rcos(θ),
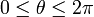
- Hence,
- x2 + w2 = r2,
-
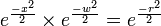 ,
,
- dx = cos(θ)dr, and
- dy = rcos(θ)dr.
- Therefore,
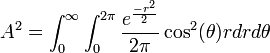 , and
, and
-
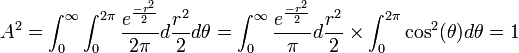 , since
, since
-
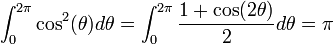 , and
, and
-
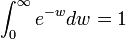 .
.
-
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:
