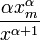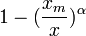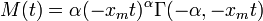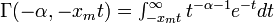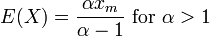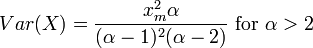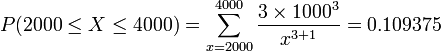AP Statistics Curriculum 2007 Pareto
From Socr
Pareto Distribution
Definition: Pareto distribution is a skewed, heavy-tailed distribution that is sometimes used to model that distribution of incomes. The basis of the distribution is that a high proportion of a population has low income while only a few people have very high incomes.
Probability density function: For 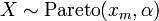 , the Pareto probability density function is given by
, the Pareto probability density function is given by
where
- xm is the minimum possible value of X
- α is a positive parameter which determines the concentration of data towards the mode
- x is a random variable (x > xm)
Cumulative density function: The Pareto cumulative distribution function is given by
where
- xm is the minimum possible value of X
- α is a positive parameter which determines the concentration of data towards the mode
- x is a random variable (x > xm)
Moment generating function: The Pareto moment-generating function is
where
Expectation: The expected value of Pareto distributed random variable x is
Variance: The Pareto variance is
Applications
The Pareto distribution is sometimes expressed more simply as the “80-20 rule”, which describes a range of situations. In customer support, it means that 80% of problems come from 20% of customers. In economics, it means 80% of the wealth is controlled by 20% of the population. Examples of events that may be modeled by Pareto distribution include:
- The sizes of human settlements (few cities, many villages)
- The file size distribution of Internet traffic which uses the TCP protocol (few larger files, many smaller files)
- Hard disk drive error rates
- The values of oil reserves in oil fields (few large fields, many small fields)
- The length distribution in jobs assigned supercomputers (few large ones, many small ones)
- The standardized price returns on individual stocks
- The sizes of sand particles
- The sizes of meteorites
- The number of species per genus
- The areas burned in forest fires
- The severity of large casualty losses for certain businesses, such as general liability, commercial auto, and workers compensation
Example
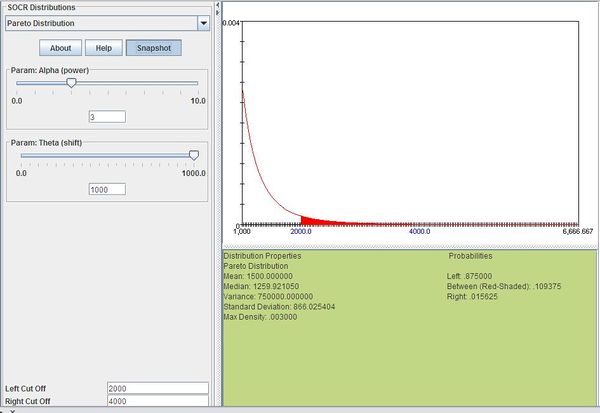
Suppose that the income of a certain population has a Pareto distribution with α = 3 and xm = 1000. Compute the proportion of the population with incomes between 2000 and 4000.
We can compute this as follows:
The figure below shows this result using SOCR distributions