AP Statistics Curriculum 2007 Prob Basics
From Socr
| Line 56: | Line 56: | ||
* Draw Ven diagram pictures of these composite events. | * Draw Ven diagram pictures of these composite events. | ||
| - | * '''Mutually exclusive''' events cannot occur at the same time (<math>A \cap B=0</math>. | + | * '''Mutually exclusive''' events cannot occur at the same time (<math>A \cap B=0</math>). |
===Axioms of probability=== | ===Axioms of probability=== | ||
| - | * First axiom: The probability of an event is a non-negative real number: <math>P(E)\geq 0 | + | * '''First axiom''': The probability of an event is a non-negative real number: <math>P(E)\geq 0</math> <math>\forall E\subseteq S</math>, where <math>S</math> is the sample space. |
| - | * Second axiom: This is the assumption of '''unit measure''': that the probability that some elementary event in the entire sample space will occur is 1. More specifically, there are no elementary events outside the sample space: <math>P( | + | * '''Second axiom''': This is the assumption of '''unit measure''': that the probability that some elementary event in the entire sample space will occur is 1. More specifically, there are no elementary events outside the sample space: <math>P(S) = 1</math>. This is often overlooked in some mistaken probability calculations; if you cannot precisely define the whole sample space, then the probability of any subset cannot be defined either. |
| - | * Third axiom: This is the assumption of additivity: Any | + | * '''Third axiom''': This is the assumption of additivity: Any countable sequence of pair-wise disjoint events <math>E_1, E_2, ...</math> satisfies <math>P(E_1 \cup E_2 \cup \cdots) = \sum_i P(E_i).</math> |
| - | * Note: For a finite sample space, a sequence of number <math>\left \{p_1, p_2, p_3, …, p_n \right \}</math> is a probability distribution for a sample space <math>S = \left \{s_1, s_2, s_3, …, s_n \right \}</math>, if the probability of the outcome <math>s_k</math>, <math>p(s_k) = p_k</math>, for each <math>1\ | + | * Note: For a finite sample space, a sequence of number <math>\left \{ p_1, p_2, p_3, …, p_n \right \}</math> is a probability distribution for a sample space <math>S = \left \{ s_1, s_2, s_3, …, s_n \right \}</math>, if the probability of the outcome <math>s_k</math>, <math>p(s_k) = p_k</math>, for each <math>1 \leq k \leq n</math>, all <math>p_k \geq 0</math> and <math>\sum_{k=1}^n{p_k}=1</math>. |
Revision as of 03:28, 29 January 2008
Contents |
General Advance-Placement (AP) Statistics Curriculum - Fundamentals of Probability Theory
Fundamentals of Probability Theory
Probability theory plays role in all studies of natural processes across scientific disciplines. The need for a theoretical probabilistic foundation is obvious since natural variation effects all measurements, observations and findings about different phenomena. Probability theory provides the basic techniques for statistical inference.
Random Sampling
A simple random sample of n items is a sample in which every member of the population has an equal chance of being selected and the members of the sample are chosen independently.
- Example: Consider a class of students as the population under study. If we select a sample of size 5, each possible sample of size 5 must have the same chance of being selected. When a sample is chosen randomly it is the process of selection that is random. How could we randomly select five members from this class randomly? Random sampling from finite (or countable) populations is well-defined. On the contrary, random sampling of uncountable populations is only allowed under the Axiom of Choice.
- Random Number Generation using SOCR: You can use SOCR Modeler to construct random samples of any size from a large number of distribution families.
- Questions:
- How would you go about randomly selecting five students from a class of 100?
- How representative of the population is the sample likely to be? The sample won’t exactly resemble the population as there will be some chance variation. This discrepancy is called chance error due to sampling.
- Definition: Sampling bias is non-randomness that refers to some members having a tendency to be selected more readily than others. When the sample is biased the statistics turn out to be poor estimates.
Hands-on activities
- Monty Hall (Three-Door) Problem: Go to SOCR Games and select the Monty Hall Game. Click in the Information button to get the instructions on using the applet. Run the game 10 times with one of two strategies:
- Stay-home strategy - choose one card first, as the computer reveals one of the donkey cards, you always stay with the card you originally chose.
- Swap strategy - choose one card first, as the computer reveals one of the donkey cards, you always swap your original guess and go with the third face-down card!
- You can try the Monty Hall Experiment, as well. There you can run a very large number of trials automatically and empirically observe the outcomes. Notice that your chance to win doubles if you use the swap-strategy. Why is that?
- See the SOCR Monty Hall Activity.
Law of Large Numbers
When studying the behavior of coin tosses, the law of large numbers implies that the relative proportion (relative frequency) of heads-to-tails in a coin toss experiment becomes more and more stable as the number of tosses increases. This regards the relative frequencies, not absolute counts of #H and #T.
- There are two widely held misconceptions about what the law of large numbers about coin tosses
- Differences between the actual numbers of heads & tails become more and more variable with increase of the number of tosses – a seq. of 10 heads doesn’t increase the chance of a tail on the next trial.
- Coin toss results are independent and fair, and the outcome behavior is unpredictable.
Types of probabilities
Probability models have two essential components: sample space and probabilities.
- Sample space (S) for a random experiment is the set of all possible outcomes of the experiment.
- An event is a collection of outcomes.
- An event occurs if any outcome making up that event occurs.
- Probabilities for each event in the sample space.
Where do the outcomes and the probabilities come from?
- Probabilities may come from models – say mathematical/physical description of the sample space and the chance of each event. Construct a fair die tossing game.
- Probabilities may be derived from data – data observations determine our probability distribution. Say we toss a coin 100 times and the observed Head/Tail counts are used as probabilities.
- Subjective Probabilities – combining data and psychological factors to design a reasonable probability table (e.g., gambling, stock market).
Event Manipulations
Just like we develop rules for numeric arithmetic, we like to use certain event-manipulation rules (event-arithmetic).
- Complement: The complement of an event A, denoted Ac or A', occurs if and only if A does not occur.
-
 , read "A or B", contains all outcomes in A or B (or both).
, read "A or B", contains all outcomes in A or B (or both).
-
 , read "A and B", contains all outcomes which are in both A and B.
, read "A and B", contains all outcomes which are in both A and B.
- Draw Ven diagram pictures of these composite events.
- Mutually exclusive events cannot occur at the same time (
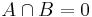 ).
).
Axioms of probability
- First axiom: The probability of an event is a non-negative real number:
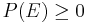
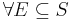 , where S is the sample space.
, where S is the sample space.
- Second axiom: This is the assumption of unit measure: that the probability that some elementary event in the entire sample space will occur is 1. More specifically, there are no elementary events outside the sample space: P(S) = 1. This is often overlooked in some mistaken probability calculations; if you cannot precisely define the whole sample space, then the probability of any subset cannot be defined either.
- Third axiom: This is the assumption of additivity: Any countable sequence of pair-wise disjoint events E1,E2,... satisfies
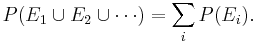
- Note: For a finite sample space, a sequence of number Failed to parse (lexing error): \left \{ p_1, p_2, p_3, …, p_n \right \}
is a probability distribution for a sample space Failed to parse (lexing error): S = \left \{ s_1, s_2, s_3, …, s_n \right \}
, if the probability of the outcome sk, p(sk) = pk, for each 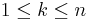 , all
, all 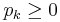 and
and 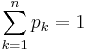 .
.
References
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:
