AP Statistics Curriculum 2007 Prob Count
From Socr
Contents |
General Advance-Placement (AP) Statistics Curriculum - Counting Principles in Probability Theory
Counting Principles in Probability Theory
There are many useful counting principles to compute the number of ways that certain arrangements of objects can be formed. Examples of such problems are counting combinations or permutations of objects. For a given collection of objects {ai}, counting methods help us describe protocols for computing numbers of arrangements of these objects when taken n at a time. For instance the number of different possible orderings of a deck of n cards is 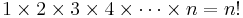 .
.
Permutations
Permutation is the rearrangement of objects or symbols into distinguishable sequences. Each unique ordering is called a permutation. For example, with the numbers {1, 2, 3, 4, 5, 6}, each possible ordering consists of a complete list of the numerals, without repetitions. There are 6!=720 total number of permutations of these numerals, one of which is: {6, 5, 4, 3, 2, 1}.
Permutations with repetitions
When the ordering of objects matters, and an object can be chosen more than once, the number of permutations is nr, where n is the number of objects from which you can choose and r is the number of objects we can choose (repetitions allowed). For example, if you have the letters A, B, C, and D and you wish to discover the number of ways to arrange them in three letter patterns, then there are 43 or 64 arrangements. Note that in this case:
- order matters (e.g., A-B is different from B-A, both are included as possibilities);
- an object can be chosen more than once (A-A possible).
This is because for the first slot you can choose any of the four values, for the second slot you can choose any of the four, and for the final slot you can choose any of the four letters. Multiplying them together gives the total.
Permutations without repetitions
When the order matters and each object can be chosen only once, then the number of permutations is 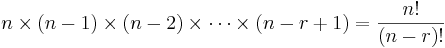 , where n is the number of objects from which you can choose, r is the number to be chosen and
, where n is the number of objects from which you can choose, r is the number to be chosen and 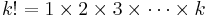 is the factorial notation. For example, if we have 5 people and we choose 3 out of the 5, we have 5!/(5 − 3)! = 60 permutations.
is the factorial notation. For example, if we have 5 people and we choose 3 out of the 5, we have 5!/(5 − 3)! = 60 permutations.
- If n = r (meaning the number of chosen elements is equal to the number of elements to choose from; we pick all 5 people) then the number of permutation becomes
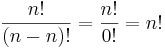 , with 0! = 1 (by definition).
, with 0! = 1 (by definition).
- If we have 5 people and want to arrange them all, the number of possible arrangements (permutations) will be 5! or 5 × 4 × 3 × 2 × 1 = 120 ways. The reason for this is that you can choose from 5 for the initial slot, then you are left with only 4 to choose from for the second slot etc. Multiplying them together gives the total of 120.
Hands-on permutation activity
This SOCR Matching Experiment demonstrates the concept of permutation. This experiment allows us to randomly permute n balls, numbered 1 to n. A match occurs whenever the ball number and the position number agree. The matches are shown in red. The number of matches N is recorded on each update. The distribution and moments of N are shown in the distribution graph and the distribution table. The parameter n can be varied with a scroll bar.
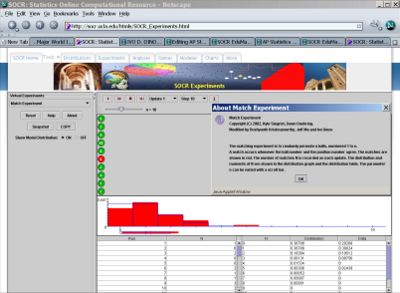
Combinations
An ordered collection of objects is a permutation. A combination is an un-ordered collection of unique objects. Given S, the set of all possible unique elements, a combination is a subset of the elements of S. The order of the elements in a combination is not important (two lists with the same elements in different orders are considered to be the same combination). Also, the elements cannot be repeated in a combination (every element appears uniquely once); i.e., we sample without replacement/repetition. Combinations are defined by the elements contained in them, thus the set {1,1,2} is the same as {2,1,1}. For example, from a 52-card deck any 5 cards can form a valid combination (a hand). The order of the cards doesn't matter and there can be no repetition of cards.
Combinations without repetitions
When the order does not matter and each object can be chosen only once, the number of combinations is the binomial coefficient: 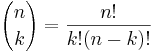 , where n is the number of objects from which you can choose and k is the number of chosen objects. For example, if you have ten numbers and wish to choose 5 you would have 10!/(5!(10 − 5)!) = 252 ways to choose. The binomial coefficient is also used to calculate the number of permutations in a lottery, as the order of the lottary numbers is irrelevant. You can use this combinations calculator to compute the combinations for
, where n is the number of objects from which you can choose and k is the number of chosen objects. For example, if you have ten numbers and wish to choose 5 you would have 10!/(5!(10 − 5)!) = 252 ways to choose. The binomial coefficient is also used to calculate the number of permutations in a lottery, as the order of the lottary numbers is irrelevant. You can use this combinations calculator to compute the combinations for  .
.
Combinations with repetitions
When the order does not matter and an object can be chosen more than once, then the number of combinations is 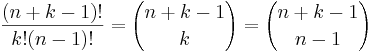 , where n is the number of objects from which you can choose and k is the number to be chosen. For example, if you have ten types of doughnuts (n) on a menu to choose from and you want three doughnuts (k) there are (10 + 3 − 1)! / 3!(10 − 1)! = 220 ways to choose.
, where n is the number of objects from which you can choose and k is the number to be chosen. For example, if you have ten types of doughnuts (n) on a menu to choose from and you want three doughnuts (k) there are (10 + 3 − 1)! / 3!(10 − 1)! = 220 ways to choose.
Hands-on activity
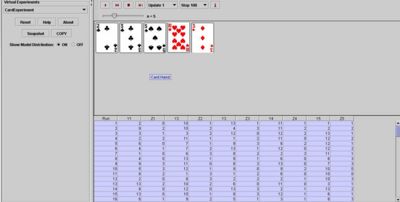
The SOCR Card Experiment allow us to see how the number of combinations may be used to estimate probabilities of various events (in terms of card hand outcomes). Suppose we are interested in the probability that all 5 cards in a randomly drawn hand are of the same suit (flush).
- Theoretical calculation: The exact probability of a flush (all 5 cards are from the same suit) is computed as follows: The number of flush hands is
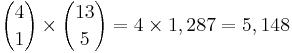 , which reflects the number of ways to select one of the 4 suits
, which reflects the number of ways to select one of the 4 suits  and the number of ways to select 5 from the 13 available card denominations
and the number of ways to select 5 from the 13 available card denominations  . The total number of 5-card poker hands is
. The total number of 5-card poker hands is 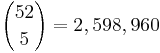 . Therefore, the probability
. Therefore, the probability 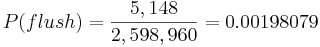 .
.
- Approximation: And we can also use the Card Experiment to estimate this probability. For example, we can run the experiment 100 times. Let T be the number of 5-card hands that had all cards of the same suit (i.e., Zi = Zj, for all
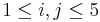 ). Then Z/100 gives a simulation-based estimate of the probability of the complex event of interest (at least one pair). Note that the values of Zi are clubs (0), diamonds (1), hearts (2) and spades (3). Thus, T is the number of rows, in the output table, that have all Z-columns having the same value (0, 1, 2, or 3). In one experiment of 100 runs, we observed one 5-card hand where all cards had the same suit. Therefore the approximate probability of a flush (the event that in a randomly chosen 5-card hand, all cards are of the same suit) is 1/100 = 0.01. This can be done by copying from the SOCR Card Applet all the rows of the output table (CNT-C) and pasting these data in an Excel spreadsheet. Then use the following function IF(MIN(C2, E2, G2, I2, K2)-MAX(C2, E2, G2,I2, K2)=0,1,0), to construct a new column (L) that looks at the Z (suit) columns and assigns 1 (5 matching suits, flush) or 0 (no flush) for each 5-card hand. At the end, the sum of the values in this column (=SUM(L2:L101)) will represent the frequency of occurrence of a flush in the sample (in this case one-hundred 5-card hands).
). Then Z/100 gives a simulation-based estimate of the probability of the complex event of interest (at least one pair). Note that the values of Zi are clubs (0), diamonds (1), hearts (2) and spades (3). Thus, T is the number of rows, in the output table, that have all Z-columns having the same value (0, 1, 2, or 3). In one experiment of 100 runs, we observed one 5-card hand where all cards had the same suit. Therefore the approximate probability of a flush (the event that in a randomly chosen 5-card hand, all cards are of the same suit) is 1/100 = 0.01. This can be done by copying from the SOCR Card Applet all the rows of the output table (CNT-C) and pasting these data in an Excel spreadsheet. Then use the following function IF(MIN(C2, E2, G2, I2, K2)-MAX(C2, E2, G2,I2, K2)=0,1,0), to construct a new column (L) that looks at the Z (suit) columns and assigns 1 (5 matching suits, flush) or 0 (no flush) for each 5-card hand. At the end, the sum of the values in this column (=SUM(L2:L101)) will represent the frequency of occurrence of a flush in the sample (in this case one-hundred 5-card hands).
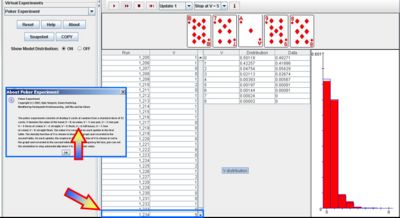
- Alternative Approximation: And we can also use the Poker Experiment to estimate the probability of a flush (V=5). Choose a stopping criterion of V=5 (this is flush). Then run the experiment. It will stop the first time you observe a flush. Therefore, 1/(number of experiments) is an estimate of the desired probability of observing a flush (see image below).
References
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:
