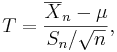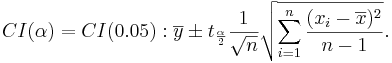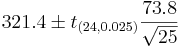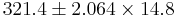AP Statistics Curriculum 2007 StudentsT
From Socr
m (→Approach III (Approximate)) |
|||
| (15 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
==[[AP_Statistics_Curriculum_2007 | General Advance-Placement (AP) Statistics Curriculum]] - Student's T Distribution== | ==[[AP_Statistics_Curriculum_2007 | General Advance-Placement (AP) Statistics Curriculum]] - Student's T Distribution== | ||
| - | Very frequently in practice we do | + | Very frequently in practice, we do not know the population variance. Therefore we need to estimate it using the sample-variance. This requires us to introduce the T-distribution, which is a one-parameter distribution connecting <math>Cauchy=T_{(df=1)} \longrightarrow T_{(df)}\longrightarrow N(0,1)=T_{(df=\infty)}</math>. |
[[Image:SOCR_Distribution_StudentT_density.JPG|200px|thumbnail|right]] | [[Image:SOCR_Distribution_StudentT_density.JPG|200px|thumbnail|right]] | ||
| Line 16: | Line 16: | ||
is normally distributed with mean 0 and variance 1, since the sample mean <math>\scriptstyle \overline{X}_n </math> is normally distributed with mean <math> \mu</math> and standard deviation <math>\scriptstyle\sigma/\sqrt{n}</math>. | is normally distributed with mean 0 and variance 1, since the sample mean <math>\scriptstyle \overline{X}_n </math> is normally distributed with mean <math> \mu</math> and standard deviation <math>\scriptstyle\sigma/\sqrt{n}</math>. | ||
| - | Gosset studied a related quantity under the pseudonym ''Student'' | + | Gosset studied a related quantity under the pseudonym ''Student'', |
:<math>T=\frac{\overline{X}_n-\mu}{S_n / \sqrt{n}},</math> | :<math>T=\frac{\overline{X}_n-\mu}{S_n / \sqrt{n}},</math> | ||
which differs from ''Z'' in that the (unknown) population standard deviation <math>\scriptstyle \sigma</math> is replaced by the sample standard deviation <math>S_n</math>. Technically, <math>\scriptstyle(n-1)S_n^2/\sigma^2</math> has a [http://en.wikipedia.org/wiki/Chi-square_distribution Chi-square distribution <math>\scriptstyle\chi_{n-1}^2</math> distribution]. Gosset's work showed that ''T'' has a specific [http://en.wikipedia.org/wiki/Student%27s_t_distribution probability density function], which approaches Normal(0,1) as the degree of freedom (df=sample-size -1) increases. | which differs from ''Z'' in that the (unknown) population standard deviation <math>\scriptstyle \sigma</math> is replaced by the sample standard deviation <math>S_n</math>. Technically, <math>\scriptstyle(n-1)S_n^2/\sigma^2</math> has a [http://en.wikipedia.org/wiki/Chi-square_distribution Chi-square distribution <math>\scriptstyle\chi_{n-1}^2</math> distribution]. Gosset's work showed that ''T'' has a specific [http://en.wikipedia.org/wiki/Student%27s_t_distribution probability density function], which approaches Normal(0,1) as the degree of freedom (df=sample-size -1) increases. | ||
| Line 26: | Line 26: | ||
===Example=== | ===Example=== | ||
| - | Suppose a researcher wants to examine [http://gateway.nlm.nih.gov/MeetingAbstracts/102282532.html CD4 counts for HIV(+) patients] seen at his clinic. She randomly selects a sample of n = 25 HIV(+) patients and measures their CD4 levels (cells/uL). Suppose she obtains the following results and we are interested in calculating a 95% (<math>\alpha=0. | + | Suppose a researcher wants to examine [http://gateway.nlm.nih.gov/MeetingAbstracts/102282532.html CD4 counts for HIV(+) patients] seen at his clinic. She randomly selects a sample of n = 25 HIV(+) patients and measures their CD4 levels (cells/uL). Suppose she obtains the following results and we are interested in calculating a 95% (<math>\alpha=0.05</math>) confidence interval for <math>\mu</math>: |
<center> | <center> | ||
| Line 43: | Line 43: | ||
: <math>n = 25</math> | : <math>n = 25</math> | ||
| - | : <math>CI(\alpha)=CI(0. | + | : <math>CI(\alpha)=CI(0.05): \overline{y} \pm t_{\alpha\over 2} {1\over \sqrt{n}} \sqrt{\sum_{i=1}^n{(x_i-\overline{x})^2\over n-1}}.</math> |
: <math>321.4 \pm t_{(24, 0.025)}{73.8\over \sqrt{25}}</math> | : <math>321.4 \pm t_{(24, 0.025)}{73.8\over \sqrt{25}}</math> | ||
| Line 64: | Line 64: | ||
*A biologist obtained body weights of male reindeer from a herd during the seasonal round-up. He measured the weight of a random sample of 102 reindeer in the herd, and found the sample mean and standard deviation to be 54.78 kg and 8.83 kg, respectively. Suppose these data come from a normal distribution. Calculate a 99% confidence interval. | *A biologist obtained body weights of male reindeer from a herd during the seasonal round-up. He measured the weight of a random sample of 102 reindeer in the herd, and found the sample mean and standard deviation to be 54.78 kg and 8.83 kg, respectively. Suppose these data come from a normal distribution. Calculate a 99% confidence interval. | ||
| - | * Suppose the proportion of blood type O in the population is 0.44. If we take a random sample of 12 subjects and make a note of their blood types | + | * Suppose the proportion of blood type O in the population is 0.44. If we take a random sample of 12 subjects and make a note of their blood types. What is the probability that exactly 6 subjects have type O blood type in the sample? |
| + | ====Approach I (exact)==== | ||
| + | : <math>P(X=6)=</math>? Where <math>X\sim B(12, 0.44)</math> | ||
| + | : <math>P(X=6)={12\choose 6}p^6(1-p)^{6}=\frac{12!}{6!(6)!}0.44^6 0.56^6=0.2068</math>, using SOCR Binomial [http://socr.ucla.edu/htmls/SOCR_Distributions.html interactive GUI] or [http://socr.ucla.edu/Applets.dir/Normal_T_Chi2_F_Tables.htm calculator]. | ||
| - | + | ====Approach II (Approximate)==== | |
| - | : <math> | + | : <math>X \sim B(n=12, p=0.44)</math>. |
| + | : <math>X (approx.) \sim N [\mu = n p = 5.28; \sigma=\sqrt{(np(1-p))}=1.7]</math>. <math>P(X=6) \approx P(Z_1\leq Z \leq Z_2)</math>, where <math>Z = {{X-5.28} \over {1.7}}</math> and <math>X_1=5.5</math>, <math>X_2=6.5</math>. So, <math>P(X=6)\approx P(Z_1 \leq Z \leq Z_2)=0.211.</math> | ||
| - | + | ====Approach III (Approximate)==== | |
| - | + | : <math>X \sim B(n=12, p=0.44)</math>. The sample proportion is <math>\hat{p} = X/n \approx N [m = p = 0.44; (p(1-p)/n)1/2=0.1433]</math>. Thus, <math>P(X=6) = P(\hat{p}=0.5) \approx P(p_1 \leq \hat{p} \leq p_2)</math>, where <math>p_1=0.5-1/24</math> and <math>p_2=0.5+1/24</math>. Note that approach II is very similar to approach III, however, the former uses the total sum of successes (X), whereas the latter employs the proportion (X/n). This is why the left-right additive term of 0.5 in approach II becomes a 0.5*(1/12) = 1/24 in the III approximation. Finally, standardize each of the 2 limits (<math>p_1</math> and <math>p_2</math>), using the <math>Z = (p-0.44)/0.1433</math> transformation, to get | |
| - | + | :<math>P(X=6) \approx P(p_1 \leq \hat{p} \leq p_2) = P(Z_1 \leq Z \leq Z_2) = 0.211.</math> | |
| - | + | ||
| - | <math>P(X=6) \approx P(p_1 \leq \hat{p} \leq p_2) = P(Z_1 \leq Z \leq Z_2) = 0.211.</math> | + | |
<hr> | <hr> | ||
| - | === | + | ===[[EBook_Problems_StudentsT|Problems]]=== |
<hr> | <hr> | ||
Current revision as of 00:18, 11 March 2011
Contents |
General Advance-Placement (AP) Statistics Curriculum - Student's T Distribution
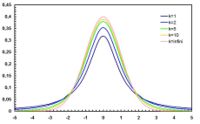
Very frequently in practice, we do not know the population variance. Therefore we need to estimate it using the sample-variance. This requires us to introduce the T-distribution, which is a one-parameter distribution connecting 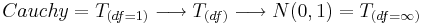 .
.
Student's T Distribution
The Student's t-distribution arises in the problem of estimating the mean of a normally distributed population when the sample size is small and the population variance is unknown. It is the basis of the popular Student's t-tests for the statistical significance of the difference between two sample means, and for confidence intervals for the difference between two population means.
Suppose X1, ..., Xn are independent random variables that are Normally distributed with expected value μ and variance σ2. Let
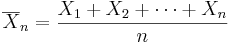 be the sample mean, and
be the sample mean, and
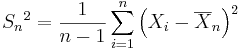 be the sample variance. We already discussed the following statistic:
be the sample variance. We already discussed the following statistic:
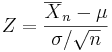
is normally distributed with mean 0 and variance 1, since the sample mean 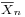 is normally distributed with mean μ and standard deviation
is normally distributed with mean μ and standard deviation 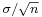 .
.
Gosset studied a related quantity under the pseudonym Student,
which differs from Z in that the (unknown) population standard deviation 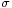 is replaced by the sample standard deviation Sn. Technically,
is replaced by the sample standard deviation Sn. Technically, 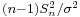 has a Chi-square distribution
has a Chi-square distribution 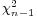 distribution. Gosset's work showed that T has a specific probability density function, which approaches Normal(0,1) as the degree of freedom (df=sample-size -1) increases.
distribution. Gosset's work showed that T has a specific probability density function, which approaches Normal(0,1) as the degree of freedom (df=sample-size -1) increases.
Computing with T-distribution
- You can see the discretized T-table or
- Use the interactive SOCR T-distribution or
- Use the high precision T-distribution calculator.
Example
Suppose a researcher wants to examine CD4 counts for HIV(+) patients seen at his clinic. She randomly selects a sample of n = 25 HIV(+) patients and measures their CD4 levels (cells/uL). Suppose she obtains the following results and we are interested in calculating a 95% (α = 0.05) confidence interval for μ:
| Variable | N | N* | Mean | SE of Mean | StDev | Minimum | Q1 | Median | Q3 | Maximum |
| CD4 | 25 | 0 | 321.4 | 14.8 | 73.8 | 208.0 | 261.5 | 325.0 | 394.0 | 449.0 |
What do we know from the background information?
-
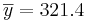
- s = 73.8
- SE = 14.8
- n = 25
- [290.85,351.95]
CI Interpretation
Still, does this CI (290.85, 351.95) mean anything to us? Consider the following information: The U.S. Government classification of AIDS has three official categories of CD4 counts – asymptomatic = greater than or equal to 500 cells/uL
- AIDS related complex (ARC) = 200-499 cells/uL
- AIDS = less than 200 cells/uL
- Now how can we interpret our CI?
SOCR CI Experiments
The SOCR Confidence Interval Experiment provides empirical evidence that the definition and the construction protocol for Confidence intervals are consistent.
Activities
- A biologist obtained body weights of male reindeer from a herd during the seasonal round-up. He measured the weight of a random sample of 102 reindeer in the herd, and found the sample mean and standard deviation to be 54.78 kg and 8.83 kg, respectively. Suppose these data come from a normal distribution. Calculate a 99% confidence interval.
- Suppose the proportion of blood type O in the population is 0.44. If we take a random sample of 12 subjects and make a note of their blood types. What is the probability that exactly 6 subjects have type O blood type in the sample?
Approach I (exact)
- P(X = 6) = ? Where
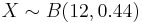
-
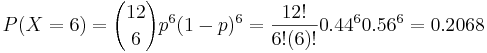 , using SOCR Binomial interactive GUI or calculator.
, using SOCR Binomial interactive GUI or calculator.
Approach II (Approximate)
-
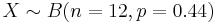 .
.
-
![X (approx.) \sim N [\mu = n p = 5.28; \sigma=\sqrt{(np(1-p))}=1.7]](/socr/uploads/math/2/6/5/265cf923bc3a2f5a8e92e3350da33f86.png) .
. 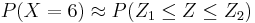 , where
, where 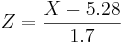 and X1 = 5.5, X2 = 6.5. So,
and X1 = 5.5, X2 = 6.5. So, 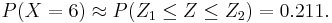
Approach III (Approximate)
-
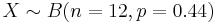 . The sample proportion is
. The sample proportion is ![\hat{p} = X/n \approx N [m = p = 0.44; (p(1-p)/n)1/2=0.1433]](/socr/uploads/math/5/c/5/5c524d421f33b9661b8b50122f7ea6c6.png) . Thus,
. Thus, 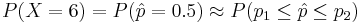 , where p1 = 0.5 − 1 / 24 and p2 = 0.5 + 1 / 24. Note that approach II is very similar to approach III, however, the former uses the total sum of successes (X), whereas the latter employs the proportion (X/n). This is why the left-right additive term of 0.5 in approach II becomes a 0.5*(1/12) = 1/24 in the III approximation. Finally, standardize each of the 2 limits (p1 and p2), using the Z = (p − 0.44) / 0.1433 transformation, to get
, where p1 = 0.5 − 1 / 24 and p2 = 0.5 + 1 / 24. Note that approach II is very similar to approach III, however, the former uses the total sum of successes (X), whereas the latter employs the proportion (X/n). This is why the left-right additive term of 0.5 in approach II becomes a 0.5*(1/12) = 1/24 in the III approximation. Finally, standardize each of the 2 limits (p1 and p2), using the Z = (p − 0.44) / 0.1433 transformation, to get
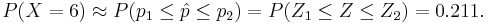
Problems
- SOCR Home page: http://www.socr.ucla.edu
Translate this page: