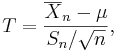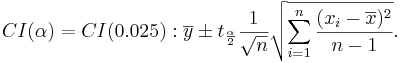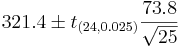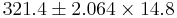AP Statistics Curriculum 2007 StudentsT
From Socr
Contents |
General Advance-Placement (AP) Statistics Curriculum - Student's T Distribution
Very frequently in practice we do now know the population variance and therefore need to estimate it using the sample-variance. This requires us to introduce the T-distribution, which is a one-parameter distribution connecting 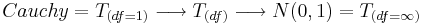 .
.
Student's T Distribution
The Student's t-distribution arises in the problem of estimating the mean of a normally distributed population when the sample size is small and the population variance is unknown. It is the basis of the popular Student's t-tests for the statistical significance of the difference between two sample means, and for confidence intervals for the difference between two population means.
Suppose X1, ..., Xn are independent random variables that are Normally distributed with expected value μ and variance σ2. Let
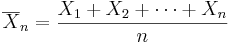 be the sample mean, and
be the sample mean, and
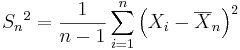 be the sample variance. We already discussed the following statistic:
be the sample variance. We already discussed the following statistic:
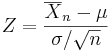
is normally distributed with mean 0 and variance 1, since the sample mean 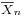 is normally distributed with mean μ and standard deviation
is normally distributed with mean μ and standard deviation 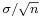 .
.
Gosset studied a related quantity under the pseudonym Student),
which differs from Z in that the (unknown) population standard deviation 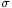 is replaced by the sample standard deviation Sn. Technically,
is replaced by the sample standard deviation Sn. Technically, 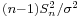 has a Chi-square distribution
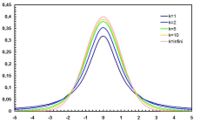
has a Chi-square distribution 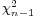 distribution. Gosset's work showed that T has a specific probability density function, which approaches Normal(0,1) as the degree of freedom (df=sample-size -1) increases.
distribution. Gosset's work showed that T has a specific probability density function, which approaches Normal(0,1) as the degree of freedom (df=sample-size -1) increases.
Computing with T-distribution
- You can see the discretized T-table or
- Use the interactive SOCR T-distribution or
- Use the high precision T-distribution calculator.
Example
Suppose a researcher wants to examine CD4 counts for HIV(+) patients seen at his clinic. She randomly selects a sample of n = 25 HIV(+) patients and measures their CD4 levels (cells/uL). Suppose she obtains the following results and we are interested in calculating a 95% (α = 0.025) confidence interval for μ:
| Variable | N | N* | Mean | SE of Mean | StDev | Minimum | Q1 | Median | Q3 | Maximum |
| CD4 | 25 | 0 | 321.4 | 14.8 | 73.8 | 208.0 | 261.5 | 325.0 | 394.0 | 449.0 |
What do we know from the background information?
-
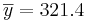
- s = 73.8
- SE = 14.8
- n = 25
- [290.85,351.95]
CI Interpretation
Still, does this CI (290.85, 351.95) mean anything to us? Consider the following information: The U.S. Government classification of AIDS has three official categories of CD4 counts – asymptomatic = greater than or equal to 500 cells/uL
- AIDS related complex (ARC) = 200-499 cells/uL
- AIDS = less than 200 cells/uL
- Now how can we interpret our CI?
SOCR CI Experiments
The SOCR Confidence Interval Experiment provides empirical evidence that the definition and the construction protocol for Confidence intervals are consistent.
Activities
- A biologist obtained body weights of male reindeer from a herd during the seasonal round-up. He measured the weight of a random sample of 102 reindeer in the herd, and found the sample mean and standard deviation to be 54.78 kg and 8.83 kg, respectively. Suppose these data come from a normal distribution. Calculate a 99% confidence interval.
- Suppose the proportion of blood type O in the population is 0.44. If we take a random sample of 12 subjects and make a note of their blood types what is the probability that exactly 6 subjects have type O blood type in the sample?
- Approach I (exact!) : P(X = 6) = ? Where
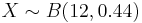
- Approach I (exact!) : P(X = 6) = ? Where
-
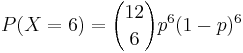 , with
, with 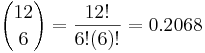 , using SOCR Binomial interactive GUI or calculator.
, using SOCR Binomial interactive GUI or calculator.
- Approach II (Approximate):
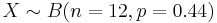
- Approach II (Approximate):
-
![X (approx.) \sim N [m = n p = 5.28; (np(1-p))1/2=1.7]](/socr/uploads/math/0/2/8/028fdbfd6dd80bef3c2072ff7e570ed0.png) .
. 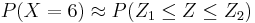 , where Failed to parse (lexing error): Z = (X – 5.28)/1.7
, where Failed to parse (lexing error): Z = (X – 5.28)/1.7
and X1 = 5.5, X2 = 6.5. So,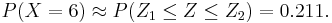
- Approach III (Approximate):
 The sample proportion is
The sample proportion is ![\hat{p} = X/n \approx N [m = p = 0.44; (p(1-p)/n)1/2=0.1433]](/socr/uploads/math/5/c/5/5c524d421f33b9661b8b50122f7ea6c6.png) Thus,
Thus, 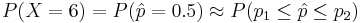 , where Failed to parse (lexing error): p_1=0.5 – 1/24
, where Failed to parse (lexing error): p_1=0.5 – 1/24
- Approach III (Approximate):
and p2 = 0.5 + 1 / 24. Standardize Z = (p − 0.44) / 0.1433 to get:
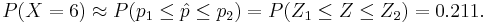
References
- SOCR Home page: http://www.socr.ucla.edu
Translate this page: