AP Statistics Curriculum 2007 Uniform
From Socr
| Line 119: | Line 119: | ||
* SOCR Home page: http://www.socr.ucla.edu | * SOCR Home page: http://www.socr.ucla.edu | ||
| - | {{translate|pageName=http://wiki.stat.ucla.edu/socr/index.php/ | + | {{translate|pageName=http://wiki.stat.ucla.edu/socr/index.php/AP_Statistics_Curriculum_2007_Uniform}} |
Current revision as of 20:18, 7 July 2011
Contents |
General Advance-Placement (AP) Statistics Curriculum - Uniform Distribution
Uniform Distribution
In the continuous uniform distribution, all intervals of the same length are equally probable. The distribution is defined by two parameters, a and b, which are the minimum and maximum values of the interval. For example, U[3,6] is the uniform distribution from 3 to 6. In the discrete uniform distribution, there are n equally spaced values, each of which have the same 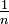 probability of being observed.
probability of being observed.
Continuous Uniform Distribution
PDF:
![\begin{cases}
\frac{1}{b - a} & \text{for } x \in [a,b] \\
0 & \text{otherwise}
\end{cases}](/socr/uploads/math/f/b/5/fb58762fb8e4aac0baa635ca7c01e65e.png)
CDF:
![\begin{cases}
0 & \text{for } x \le a \\
\frac{x-a}{b-a} & \text{for } x \in [a,b] \\
1 & \text{for } x \ge b
\end{cases}](/socr/uploads/math/5/d/4/5d4d74273bca95256fa860612db73c3d.png)
Mean:
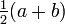
Median:
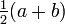
Mode:
any value in [a,b]
Variance:
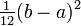
Support:
![x \in [a,b]](/socr/uploads/math/8/2/9/8290bddba5acf9822dcbf61f4ac67d1b.png)
Moment Generating Function:
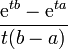
Discrete Uniform Distribution
PDF:
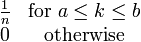
CDF:
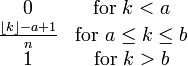
Mean:
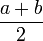
Median:
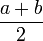
Mode:
N/A
Variance:
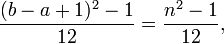
Support:
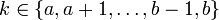
Moment Generating Function:
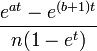
Applications
Generation of random numbers. Random numbers are often generated from a uniform distribution U[0,1]
In R, to generate 5 random integers from [1:10] with replacement:
> sample(1:10, 5, replace = TRUE)
Example (Continuous)
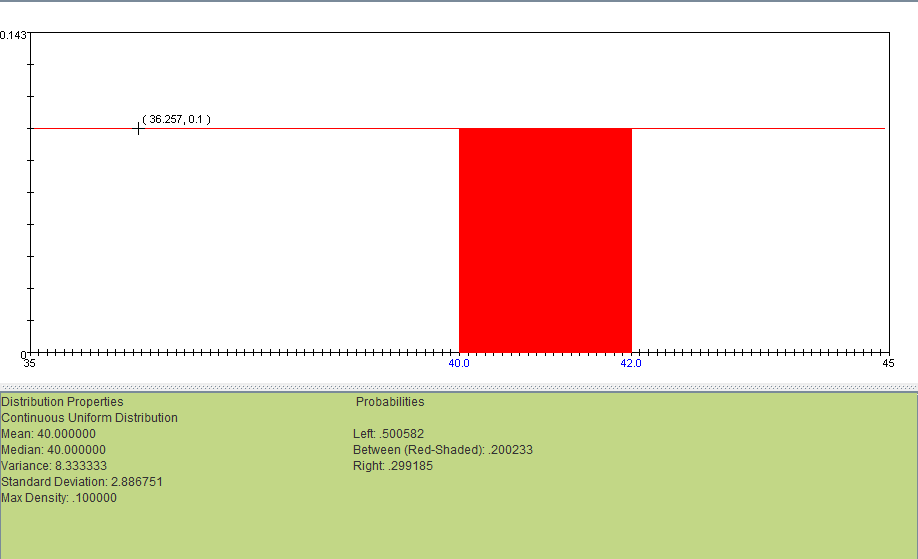
It is known that the time to complete an oil change at a certain dealership is random and takes between 35 to 45 minutes. If you take your car to this dealership to get an oil change, what is the probability that it will take between 40 to 42 minutes?
Answer:
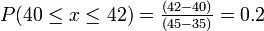
Example (Discrete)
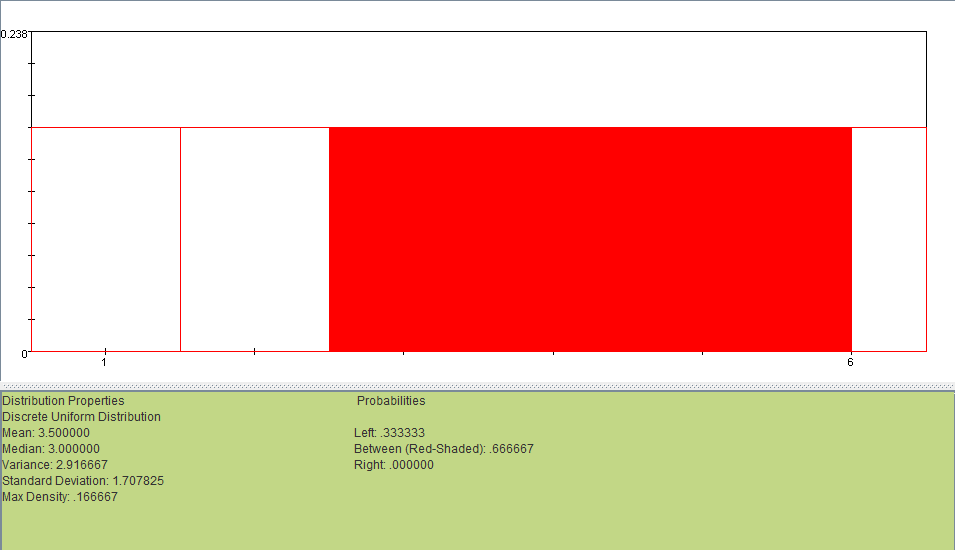
If you throw a fair six sided die, what is the probability that you get a number greater than 2?
Answer:
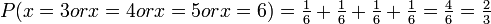
SOCR Links
http://www.distributome.org/ -> SOCR -> Distributions -> Distributome
http://www.distributome.org/ -> SOCR -> Distributions -> Continuous Uniform Distribution
http://www.distributome.org/ -> SOCR -> Distributions -> Discrete Uniform Distribution
http://www.distributome.org/ -> SOCR -> Functors -> Continuous Uniform Distribution
http://www.distributome.org/ -> SOCR -> Functors -> Discrete Uniform Distribution
http://www.distributome.org/ -> SOCR -> Experiments -> Uniform Estimate Experiment
http://www.distributome.org/ -> SOCR -> Experiments -> Uniform E-Estimate Experiment
SOCR Uniform Distributions calculators:
 http://socr.ucla.edu/htmls/dist/ContinuousUniform_Distribution.html
http://socr.ucla.edu/htmls/dist/ContinuousUniform_Distribution.html
 http://socr.ucla.edu/htmls/dist/DiscreteUniform_Distribution.html
http://socr.ucla.edu/htmls/dist/DiscreteUniform_Distribution.html
- SOCR Home page: http://www.socr.ucla.edu
Translate this page: