EBook Problems
From Socr
(→Testing a Claim about a Mean: Small Samples) |
(→Testing a Claim about a Proportion) |
||
| Line 189: | Line 189: | ||
==[[AP_Statistics_Curriculum_2007_Hypothesis_Proportion |Testing a Claim about a Proportion]]== | ==[[AP_Statistics_Curriculum_2007_Hypothesis_Proportion |Testing a Claim about a Proportion]]== | ||
When the sample size is large, the sampling distribution of the sample proportion <math>\hat{p}</math> is approximately Normal, by [[AP_Statistics_Curriculum_2007_Limits_CLT | CLT]]. This helps us formulate hypothesis testing protocols and compute the appropriate statistics and p-values to assess significance. | When the sample size is large, the sampling distribution of the sample proportion <math>\hat{p}</math> is approximately Normal, by [[AP_Statistics_Curriculum_2007_Limits_CLT | CLT]]. This helps us formulate hypothesis testing protocols and compute the appropriate statistics and p-values to assess significance. | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
===[[EBook_Problems_Hypothesis_Proportion | Problems]]=== | ===[[EBook_Problems_Hypothesis_Proportion | Problems]]=== | ||
Revision as of 07:46, 27 November 2008
Probability and Statistics EBook Practice Problems
The problems provided below may be useful for practicing the concepts, methods and analysis protocols, and for self-evaluation of learning of the materials presented in the EBook.
I. Introduction to Statistics
The Nature of Data and Variation
Although natural phenomena in real life are unpredictable, the designs of experiments are bound to generate data that varies because of intrinsic (internal to the system) or extrinsic (due to the ambient environment) effects. How many natural processes or phenomena in real life can we describe that have an exact mathematical closed-form description and are completely deterministic? How do we model the rest of the processes that are unpredictable and have random characteristics?
Problems
Uses and Abuses of Statistics
Statistics is the science of variation, randomness and chance. As such, statistics is different from other sciences, where the processes being studied obey exact deterministic mathematical laws. Statistics provides quantitative inference represented as long-time probability values, confidence or prediction intervals, odds, chances, etc., which may ultimately be subjected to varying interpretations. The phrase Uses and Abuses of Statistics refers to the notion that in some cases statistical results may be used as evidence to seemingly opposite theses. However, most of the time, common principles of logic allow us to disambiguate the obtained statistical inference.
Problems
Design of Experiments
Design of experiments is the blueprint for planning a study or experiment, performing the data collection protocol and controlling the study parameters for accuracy and consistency. Data, or information, is typically collected in regard to a specific process or phenomenon being studied to investigate the effects of some controlled variables (independent variables or predictors) on other observed measurements (responses or dependent variables). Both types of variables are associated with specific observational units (living beings, components, objects, materials, etc.)
Problems
Statistics with Tools (Calculators and Computers)=
All methods for data analysis, understanding or visualizing are based on models that often have compact analytical representations (e.g., formulas, symbolic equations, etc.) Models are used to study processes theoretically. Empirical validations of the utility of models are achieved by inputting data and executing tests of the models. This validation step may be done manually, by computing the model prediction or model inference from recorded measurements. This process may be possible by hand, but only for small numbers of observations (<10). In practice, we write (or use existent) algorithms and computer programs that automate these calculations for better efficiency, accuracy and consistency in applying models to larger datasets.
Problems
II. Describing, Exploring, and Comparing Data
Types of Data
There are two important concepts in any data analysis - Population and Sample. Each of these may generate data of two major types - Quantitative or Qualitative measurements.
Problems
Summarizing Data with Frequency Tables
There are two important ways to describe a data set (sample from a population) - Graphs or Tables.
Problems
Pictures of Data
There are many different ways to display and graphically visualize data. These graphical techniques facilitate the understanding of the dataset and enable the selection of an appropriate statistical methodology for the analysis of the data.
Problems
Measures of Central Tendency
There are three main features of populations (or sample data) that are always critical in understanding and interpreting their distributions - Center, Spread and Shape. The main measures of centrality are Mean, Median and Mode(s).
Problems
Measures of Variation
There are many measures of (population or sample) spread, e.g., the range, the variance, the standard deviation, mean absolute deviation, etc. These are used to assess the dispersion or variation in the population.
Problems
Measures of Shape
The shape of a distribution can usually be determined by looking at a histogram of a (representative) sample from that population; Frequency Plots, Dot Plots or Stem and Leaf Displays may be helpful.
Problems
Statistics
Variables can be summarized using statistics - functions of data samples.
Problems
Graphs and Exploratory Data Analysis
Graphical visualization and interrogation of data are critical components of any reliable method for statistical modeling, analysis and interpretation of data.
Problems
III. Probability
Probability is important in many studies and disciplines because measurements, observations and findings are often influenced by variation. In addition, probability theory provides the theoretical groundwork for statistical inference.
Fundamentals
Some fundamental concepts of probability theory include random events, sampling, types of probabilities, event manipulations and axioms of probability.
Problems
Rules for Computing Probabilities
There are many important rules for computing probabilities of composite events. These include conditional probability, statistical independence, multiplication and addition rules, the law of total probability and the Bayesian rule.
Problems
Probabilities Through Simulations
Many experimental setting require probability computations of complex events. Such calculations may be carried out exactly, using theoretical models, or approximately, using estimation or simulations.
Problems
Counting
There are many useful counting principles (including permutations and combinations) to compute the number of ways that certain arrangements of objects can be formed. This allows counting-based estimation of probabilities of complex events.
Problems
IV. Probability Distributions
There are two basic types of processes that we observe in nature - Discrete and Continuous. We begin by discussing several important discrete random processes, emphasizing the different distributions, expectations, variances and applications. In the next chapter, we will discuss their continuous counterparts. The complete list of all SOCR Distributions is available here.
Random Variables
To simplify the calculations of probabilities, we will define the concept of a random variable which will allow us to study uniformly various processes with the same mathematical and computational techniques.
Problems
Expectation (Mean) and Variance
The expectation and the variance for any discrete random variable or process are important measures of Centrality and Dispersion. This section also presents the definitions of some common population- or sample-based moments.
Problems
Bernoulli and Binomial Experiments
The Bernoulli and Binomial processes provide the simplest models for discrete random experiments.
Problems
Multinomial Experiments
Multinomial processes extend the Binomial experiments for the situation of multiple possible outcomes.
Problems
Geometric, Hypergeometric and Negative Binomial
The Geometric, Hypergeometric and Negative Binomial distributions provide computational models for calculating probabilities for a large number of experiment and random variables. This section presents the theoretical foundations and the applications of each of these discrete distributions.
Problems
Poisson Distribution
The Poisson distribution models many different discrete processes where the probability of the observed phenomenon is constant in time or space. Poisson distribution may be used as an approximation to the Binomial distribution.
Problems
V. Normal Probability Distribution
The Normal Distribution is perhaps the most important model for studying quantitative phenomena in the natural and behavioral sciences - this is due to the Central Limit Theorem. Many numerical measurements (e.g., weight, time, etc.) can be well approximated by the normal distribution.
The Standard Normal Distribution
The Standard Normal Distribution is the simplest version (zero-mean, unit-standard-deviation) of the (General) Normal Distribution. Yet, it is perhaps the most frequently used version because many tables and computational resources are explicitly available for calculating probabilities.
Problems
Nonstandard Normal Distribution: Finding Probabilities
In practice, the mechanisms underlying natural phenomena may be unknown, yet the use of the normal model can be theoretically justified in many situations to compute critical and probability values for various processes.
Problems
Nonstandard Normal Distribution: Finding Scores (Critical Values)
In addition to being able to compute probability (p) values, we often need to estimate the critical values of the Normal Distribution for a given p-value.
Problems
VI. Relations Between Distributions
In this chapter, we will explore the relations between different distributions. This knowledge will help us to compute difficult probabilities using reasonable approximations and identify appropriate probability models, graphical and statistical analysis tools for data interpretation. The complete list of all SOCR Distributions is available here and the SOCR Distributome applet provides an interactive graphical interface for exploring the relations between different distributions.
The Central Limit Theorem
The exploration of the relation between different distributions begins with the study of the sampling distribution of the sample average. This will demonstrate the universally important role of normal distribution.
Problems
Law of Large Numbers
Suppose the relative frequency of occurrence of one event whose probability to be observed at each experiment is p. If we repeat the same experiment over and over, the ratio of the observed frequency of that event to the total number of repetitions converges towards p as the number of experiments increases. Why is that and why is this important?
Problems
Normal Distribution as Approximation to Binomial Distribution
Normal Distribution provides a valuable approximation to Binomial when the sample sizes are large and the probability of successes and failures are not close to zero.
Problems
Poisson Approximation to Binomial Distribution
Poisson provides an approximation to Binomial Distribution when the sample sizes are large and the probability of successes or failures is close to zero.
Problems
Binomial Approximation to Hypergeometric
Binomial Distribution is much simpler to compute, compared to Hypergeometric, and can be used as an approximation when the population sizes are large (relative to the sample size) and the probability of successes is not close to zero.
Problems
Normal Approximation to Poisson
The Poisson can be approximated fairly well by Normal Distribution when λ is large.
Problems
VII. Point and Interval Estimates
Estimation of population parameters is critical in many applications. Estimation is most frequently carried in terms of point-estimates or interval (range) estimates for population parameters that are of interest.
Method of Moments and Maximum Likelihood Estimation
There are many ways to obtain point (value) estimates of various population parameters of interest, using observed data from the specific process we study. The method of moments and the maximum likelihood estimation are among the most popular ones frequently used in practice.
Problems
Estimating a Population Mean: Large Samples
This section discusses how to find point and interval estimates when the sample-sizes are large.
Problems
Estimating a Population Mean: Small Samples
Next, we discuss point and interval estimates when the sample-sizes are small. Naturally, the point estimates are less precise and the interval estimates produce wider intervals, compared to the case of large-samples.
Problems
Student's T distribution
The Student's T-Distribution arises in the problem of estimating the mean of a normally distributed population when the sample size is small and the population variance is unknown.
Problems
Estimating a Population Proportion
Normal Distribution is appropriate model for proportions, when the sample size is large enough. In this section, we demonstrate how to obtain point and interval estimates for population proportion.
Problems
Estimating a Population Variance
In many processes and experiments, controlling the amount of variance is of critical importance. Thus the ability to assess variation, using point and interval estimates, facilitates our ability to make inference, revise manufacturing protocols, improve clinical trials, etc.
Problems
VIII. Hypothesis Testing
Hypothesis Testing is a statistical technique for decision making regarding populations or processes based on experimental data. It quantitatively answers the possibility that chance alone might be responsible for the observed discrepancy between a theoretical model and the empirical observations.
Fundamentals of Hypothesis Testing
In this section, we define the core terminology necessary to discuss Hypothesis Testing (Null and Alternative Hypotheses, Type I and II errors, Sensitivity, Specificity, Statistical Power, etc.)
Problems
Testing a Claim about a Mean: Large Samples
As we already saw how to construct point and interval estimates for the population mean in the large sample case, we now show how to do hypothesis testing in the same situation.
Problems
Testing a Claim about a Mean: Small Samples
We continue with the discussion on inference for the population mean for small samples.
Problems
Testing a Claim about a Proportion
When the sample size is large, the sampling distribution of the sample proportion 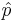 is approximately Normal, by CLT. This helps us formulate hypothesis testing protocols and compute the appropriate statistics and p-values to assess significance.
is approximately Normal, by CLT. This helps us formulate hypothesis testing protocols and compute the appropriate statistics and p-values to assess significance.
Problems
Testing a Claim about a Standard Deviation or Variance
The significance testing for the variation or the standard deviation of a process, a natural phenomenon or an experiment is of paramount importance in many fields. This chapter provides the details for formulating testable hypotheses, computation, and inference on assessing variation.
Problems
IX. Inferences from Two Samples
In this chapter, we continue our pursuit and study of significance testing in the case of having two populations. This expands the possible applications of one-sample hypothesis testing we saw in the previous chapter.
Inferences About Two Means: Dependent Samples
We need to clearly identify whether samples we compare are Dependent or Independent in all study designs. In this section, we discuss one specific dependent-samples case - Paired Samples.
Problems
Inferences About Two Means: Independent Samples
Independent Samples designs refer to experiments or observations where all measurements are individually independent from each other within their groups and the groups are independent. In this section, we discuss inference based on independent samples.
Problems
Comparing Two Variances
In this section, we compare variances (or standard deviations) of two populations using randomly sampled data.
Problems
Inferences about Two Proportions
This section presents the significance testing and inference on equality of proportions from two independent populations.
Problems
X. Correlation and regression
Many scientific applications involve the analysis of relationships between two or more variables involved in a process of interest. We begin with the simplest of all situations where Bivariate Data (X and Y) are measured for a process and we are interested on determining the association, relation or an appropriate model for these observations (e.g., fitting a straight line to the pairs of (X,Y) data).
Correlation
The Correlation between X and Y represents the first bivariate model of association which may be used to make predictions.
1. A positive correlation between two variables X and Y means that if X increases, this will cause the value of Y to increase.
- (a) This is always true.
- (b) This is sometimes true.
- (c) This is never true.
2. The correlation between high school algebra and geometry scores was found to be + 0.8. Which of the following statements is not true?
- (a) Most of the students who have above average scores in algebra also have above average scores in geometry.
- (b) Most people who have above average scores in algebra will have below average scores in geometry
- (c) If we increase a student's score in algebra (ie. with extra tutoring in algebra), then the student's geometry scores will always increase accordingly.
- (d) Most students who have below average scores in algebra also have below average scores in geometry.
3. Researchers discover that the correlation between miles ran per week and cardiovascular endurance is +0.75. They also discover that the correlation between hours spent watching television per week and cardiovascular endurance is -0.75. What is the conclusion that best characterizes the result of this study?
Choose one answer.
- (a) Most people who spend a lot of hours watching television have low cardiovascular endurance.
- (b) Most people who have good cardiovascular endurance spend a lot of time running and little time watching television.
- (c) Based on the correlation, if you increase your running hours per week, your cardiovascular endurance will decrease.
- (d) Based on the correlation, if you increases your television watching time, your cardiovascular endurance will decrease.
- (e) Most people with a lot of miles ran per week have high cardiovascular endurance.
4. The correlation between working out and body fat was found to be exactly -1.0. Which of the following would not be true about the corresponding scatterplot?
Choose one answer.
- (a) The slope of the best line of fit should be -1.0.
- (b) All the points would lie along a perfect straight line, with no deviation at all.
- (c) The best fitting line would have a downhill (negative) slope.
- (d) 100% of the variance in body fat can be predicted from workout.
5. Suppose that the correlation between working out and body fat was found to be exactly -1.0. Which of the following would NOT be true, about the corresponding scatterplot?
Choose one answer.
- (a) All points would lie along a straight line, with no deviation at all.
- (b) 100% of the variance in body fat can be predicted from the workout.
- (c) The slope of the linear model is -1.0.
- (d) The best fitting line would have a negative slope.
6. A recent article in an educational research journal reports a correlation of +0.8 between math achievement and overall math aptitude. It also reports a correlation of -0.8 between math achievement and a math anxiety test. Which of the following interpretations is the most correct?
Choose one answer
- (a) You cannot compare a positive and a negative correlation.
- (b) The correlation of +0.8 indicates a stronger relationship than the correlation of -0.8.
- (c) The correlation of +0.8 is just as strong as the correlation of -0.8.
- (d) It is impossible to tell which correlation is stronger.
7. Psychologists have shown that there is a relationship between stress levels and productivity. As stress levels increase, productivity also increases up to a certain point, and after that productivity decreases as stress levels increase. Suppose you were given this data for a random sample of 200 adults. If you calculated the Pearson coefficient of correlation, what would you expect to find?
Choose one answer.
- (a) I would expect r to be between -0.50 to -0.70.
- (b) I would expect r to be -1.
- (c) I would expect r to be between 0.50 and 0.70.
- (d) I would expect r to be +1.
- (e) I would expect r to be zero.
8. If the correlation coefficient is 0.80, then:
Choose one answer.
- (a) The explanatory variable is usually less than the response variable.
- (b) The explanatory variable is usually more than the response variable.
- (c) None of the statements are correct.
- (d) Below-average values of the explanatory variable are more often associated with below-average values of the response variable.
- (e) Below-average values of the explanatory variable are more often associated with above-average values of the response variable.
9. Given the following data, what is the best estimate for the coefficient of correlation between the ages of the husbands and wives?
There are 50 couples (husband and wife). The age range for men is from 50 to 70 years old. The age range for women is from 48 to 68 years old. For all of the couples, the husband is two years older than the wife. For instance, in one couple the husband is 50 years old and the wife is 48 years old.
Choose one answer.
- (a) The coefficient of correlation between the age of husband and wife is equal to +1.
- (b) We need the actual data to compute the coefficient of correlatin between the age of the husband and wife.
- (c) The coefficient of correlation between the age of husband and wife is equal to zero.
- (d) The coefficient of correlation between the age of husband and wife is equal to +0.50.
- (e) The coefficient of correlation between the age of husband and wife is equal to -1.
Problems
Regression
We are now ready to discuss the modeling of linear relations between two variables using Regression Analysis. This section demonstrates this methodology for the SOCR California Earthquake dataset.
1. Use the information from the Heights of Fathers and Sons to write the linear model that best predicts the height of the son from the height of the father.
Choose one answer.
- (a) Son's height = 35 + 0.5*Father's height'
- (b) Son's height = 1.00 + 1.00* Father's height
- (c) The model cannot be determined without the actual data
- (d) Son's height = 0.5 + 35*Father's height
2. A congressional report investigates the relationship between income of parents and educational attainment of their daughters. Data are from a sample of families with daughters age 18-24. Average parental income is $29,300, average educational attainment of the daughters is 13.1 years of schooling completed, and the correlation is 0.37.
The regression line for predicting daughter’s education from parental income is reported as: Predicted education = 0.000617*(income) + 8.1
Is the following statement true or false? "The above line is the regression line to predict education from income."
- (a)True.
- (b)False.
3. Heights of Fathers and Sons
In the early 1900's when Francis Galton and Karl Pearson measured 1078 pairs of fathers and their grown-up sons, they calculated that the mean height for fathers was about 68 inches with deviation of 3 inches. For their sons, the mean height was 69 inches with deviation of 3 inches. (The actual numbers are slightly smaller, but we will work with these values to keep the calculations simple.) The correlation coefficient was 0.50. Use the information to calculate the slope of the linear model that predicts the height of the son from the height of the father.
Choose one answer.
- (a) 0.50
- (b) The slope cannot be determined without the actual data
- (c) 35.00
- (d) 3/3 = 1.00
4. The National Highway Safety Administration is interested in the effect of seat belt use on saving lives. One study reported statistics on children under the age of 5 who were involved in motor vehicles accidents in which at least one fatality occurred. 7,060 such accidents between 1985 and 1989 were studied. Of those who survived, 1129 weren't wearing a seat belt, 432 were wearing an adult seat belt and 733 had a children's carseat belt. Of those with fatalities, 509 had no belt, 73 had an adult seat belt, and 139 had a children's carseat belt.
Are seat belt status and the outcome of the accidents independent?
Choose one answer.
- (a) Yes
- (b) No
- (c) Can't tell with the information provided
5. Suppose that wildlife researchers monitor the local alligator population by taking aerial photograhs on a regular schedule. They determine that the best fitting linear model to predict weight in pounds from the length of the gators inches is:
Weight = -393 + 5.9*Length with r2 = 0.836.
Which of the following statements is true?
Choose one answer.
- (a) A gator that is about 10 inches above average in length is about 59 pounds above the average weight of these gators.
- (b) The correlation between a gator's length and weight is 0.836.
- (c) The correlation between a gator's height and weight cannot be determined without the actual data.
- (d) The correlation between a gator's height and weigth is about -0.914.
Problems
Variation and Prediction Intervals
In this section, we discuss point and interval estimates about the slope of linear models.
1. Two researchers are going to take a sample of data from the same population of physics students. Researcher A will select a random sample of students from among all students taking physics. Researcher B's sample will consist only of the students in her class. Both researchers will construct a 95% confidence interval for the mean score on the physics final exam using their own sample data. Which researcher's method has a 95% chance of capturing the true mean of the population of all students taking physics?
Choose one answer.
- (a) Research B
- (b) Researcher A
- (c) Both methods have a 95% chance of capturing the true mean
- (d) Neither
2. A random sample of 150 UCLA students found that 35% of the respondants wanted a elevator to replace Bruin Walk. A 95% confidence interval for the percentage of all UCLA students who feel this way is approximately:
Choose one answer.
- (a) (24%, 46%)
- (b) (32%, 38%)
- (c) The sample size is too small to compute a confidence interval.
- (d) (27%, 43%)
3. According to Terry Prachett, the short unit of time in the multiverse is the New York second, defined as the time interval between the light turning green and the cab behind you honking. A magazine took a poll of 100 New Yorkers and found that 90 people agree with that statement wholeheartedly. Which of the following is a 90% confidence interval for the proportion of people who agree with that statement?
Choose one answer.
- (a) 0.9 +\- 0.50
- (b) 0.9 +\- .05
- (c) 0.9 +\- .03
- (d) 0.9 +\- .06
4. A national poll found that 62% of all Americans agreed that more attention should be paid to mental health of war veterans. If a simple random sample of 326 people was used to make a 95% confidence interval of (0.57,0.67), what is the margin of error?
Choose one answer.
- (a) 0.03
- (b) 0.05
- (c) 0.12
- (d) In order to calculate the margin of error, we need the p-value of the population.
5. Hermione Granger is on a mission this year to complain about the astronomical cost of wizarding books to the Hogwart board of administrators. Given that the population mean for book cost is 10 and a standard deviation of 2 galleons, If Hermione were to take a simple random sample of 49 students and make a 68% confidence interval, what would be the range of values for the sample mean or Xbar?
Choose one answer.
- (a) 8 and 12 galleons
- (b) 9.4 and 10.6 galleons
- (c) 6 and 14 Galleons
- (d) 9.7 and 10.3 galleons
6. A 95% confidence interval indicates that:
Choose one answer:
- (a) 95% of the intervals constructed using this process based on samples from this population will include the population mean
- (b) 95% of the time the interval will include the sample mean
- (c) 95% of the possible population means will be included by the interval
- (d) 95% of the possible sample means will be included by the interval
7. Suppose we want to find out if a coin is not fair. To test this hypothesis we flip the coin 100 times, and in 63 out of 100 flips we get heads. We construct the confidence interval and find it to be (.53,.73). Interpret this confidence interval.
Choose one answer.
- (a) 95 is the Z score that corresponds to our distribution of sample means
- (b) Confidence is something you learn at fraternity parties
- (c) 95% of the time the true proportion of flips that are heads is between .53 and .73
- (d) If we were to repeat this expirement over and over again, 95 times out of 100 our Confidence interval would cover the true proportion of flips that are heads
8. A 95% confidence interval is calculated for a sample of weights of 100 randomly selected pigs, and is (42 pounds, 48 pounds). Will the sample mean weight fall within the confidence interval?
Choose one answer.
- (a) Yes
- (b) We need more information to determine if this is true.
- (c) No
9. The average number of fruit candies in a large bag is estimated. The 95% confidence interval is (40, 48). Based on this information, you know that the best estimate of the population mean is:
Choose one answer.
- (a) 43
- (b) 40
- (c) 45
- (d) none of the above.
- (e) 44
10. Suppose we plan to take a random sample of adults in the U.S. and determine the percent of them who have attended church in the last 30 days. We calculate a 90% confidence interval for the proportion of all adults in the U.S. who attended church in the last 30 days. Which of the following changes in our plans would result in a wider confidence interval? Check all that apply.
Choose one answer.
- (a) Using an 85% confidence level.
- (b) Using a 95% confidence level.
- (c) Using a larger sample.
- (d) Using a smaller sample.
11. Kevin has always, ever since he was a wee lad, wondered what proportion of the candies in M&M chocolate candies bags are yellow. However, his persistent calls to the M&M headquarter were of no avail. Now that he wields the awesome power of being a TA for Stat 10, he makes each of his 200 students go buy a M&M bag, count the colors, and compute a 99% confidence intervals for the yellow candy proportion. Assume that each M&M bag is a random sample, approximately how many of the 200 confidence intervals will not capture the true population proportion for yellow M&M's?
Choose one answer.
- (a) Not enough information for an answer
- (b) 0 to 4
- (c) 4 to 8
- (d) 12 to 14
- (e) 8 to 12
12. A 95% confidence interval for the proportion of U.S. adults who favor the death penalty is given by (0.03, 0.09). Is the following statement true or false?
"There is a 95% probability that an adult in the US is in favor of the death penalty."
- (a) True
- (b) False
Problems
Multiple Regression
Now, we are interested in determining linear regressions and multilinear models of the relationships between one dependent variable Y and many independent variables Xi.
Problems
XI. Analysis of Variance (ANOVA)
One-Way ANOVA
We now expand our inference methods to study and compare k independent samples. In this case, we will be decomposing the entire variation in the data into independent components.
Problems
Two-Way ANOVA
Now we focus on decomposing the variance of a dataset into (independent/orthogonal) components when we have two (grouping) factors. This procedure called Two-Way Analysis of Variance.
Problems
XII. Non-Parametric Inference
To be valid, many statistical methods impose (parametric) requirements about the format, parameters and distributions of the data to be analyzed. For instance, the Independent T-Test requires the distributions of the two samples to be Normal, whereas Non-Parametric (distribution-free) statistical methods are often useful in practice, and are less-powerful.
Differences of Medians (Centers) of Two Paired Samples
The Sign Test and the Wilcoxon Signed Rank Test are the simplest non-parametric tests which are also alternatives to the One-Sample and Paired T-Test. These tests are applicable for paired designs where the data is not required to be normally distributed.
Problems
Differences of Medians (Centers) of Two Independent Samples
The Wilcoxon-Mann-Whitney (WMW) Test (also known as Mann-Whitney U Test, Mann-Whitney-Wilcoxon Test, or Wilcoxon rank-sum Test) is a non-parametric test for assessing whether two samples come from the same distribution.
Problems
Differences of Proportions of Two Samples
Depending upon whether the samples are dependent or independent, we use different statistical tests.
Problems
Differences of Means of Several Independent Samples
We now extend the multi-sample inference which we discussed in the ANOVA section, to the situation where the ANOVA assumptions are invalid.
Problems
Differences of Variances of Independent Samples (Variance Homogeneity)
There are several tests for variance equality in k samples. These tests are commonly known as tests for Homogeneity of Variances.
Problems
XIII. Multinomial Experiments and Contingency Tables
Multinomial Experiments: Goodness-of-Fit
The Chi-Square Test is used to test if a data sample comes from a population with specific characteristics.
Problems
Contingency Tables: Independence and Homogeneity
The Chi-Square Test may also be used to test for independence (or association) between two variables.
Problems
References
Translate this page:
