Formulas
From Socr
(Difference between revisions)
(added Chi PDF) |
|||
| Line 1: | Line 1: | ||
This [[Main_Page | SOCR Wiki]] page contains a number of formulas, mathematical expressions and symbolic representations that are used in varieties of SOCR resources. Usage is defined as a reference by image, text, TeX, URL, etc. For instance the [http://socr.ucla.edu/htmls/SOCR_Distributome.html SOCR Distributome project] uses these formulas to represent PDFs, CDFs, transformations, etc. | This [[Main_Page | SOCR Wiki]] page contains a number of formulas, mathematical expressions and symbolic representations that are used in varieties of SOCR resources. Usage is defined as a reference by image, text, TeX, URL, etc. For instance the [http://socr.ucla.edu/htmls/SOCR_Distributome.html SOCR Distributome project] uses these formulas to represent PDFs, CDFs, transformations, etc. | ||
| + | |||
| + | ==Probability Density Functions (PDFs)== | ||
* [[AP_Statistics_Curriculum_2007_Normal_Std |Standard Normal]] PDF: <math>f(x)= {e^{-x^2} \over \sqrt{2 \pi}}</math> | * [[AP_Statistics_Curriculum_2007_Normal_Std |Standard Normal]] PDF: <math>f(x)= {e^{-x^2} \over \sqrt{2 \pi}}</math> | ||
| Line 9: | Line 11: | ||
* [[AP_Statistics_Curriculum_2007_Distrib_Poisson | Poisson]] PDF: <math>\frac{e^{-\lambda} \lambda^k}{k!}\!</math> | * [[AP_Statistics_Curriculum_2007_Distrib_Poisson | Poisson]] PDF: <math>\frac{e^{-\lambda} \lambda^k}{k!}\!</math> | ||
* [http://en.wikipedia.org/wiki/Chi_distribution Chi] PDF: <math>\frac{2^{1-k/2}x^{k-1}e^{-x^2/2}}{\Gamma(k/2)}</math> | * [http://en.wikipedia.org/wiki/Chi_distribution Chi] PDF: <math>\frac{2^{1-k/2}x^{k-1}e^{-x^2/2}}{\Gamma(k/2)}</math> | ||
| + | |||
| + | ==Transformations== | ||
| + | * TBD | ||
| + | |||
| + | <hr> | ||
| + | * SOCR Home page: http://www.socr.ucla.edu | ||
| + | |||
| + | {{translate|pageName=http://wiki.stat.ucla.edu/socr/index.php?title=Formulas}} | ||
Revision as of 19:32, 24 April 2008
This SOCR Wiki page contains a number of formulas, mathematical expressions and symbolic representations that are used in varieties of SOCR resources. Usage is defined as a reference by image, text, TeX, URL, etc. For instance the SOCR Distributome project uses these formulas to represent PDFs, CDFs, transformations, etc.
Probability Density Functions (PDFs)
- Standard Normal PDF:
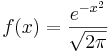
- General Normal PDF:
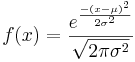
- Chi-Square PDF:
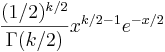
- Gamma PDF:
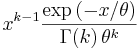
- Beta PDF:
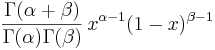
- Student's T PDF:
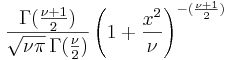
- Poisson PDF:
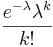
- Chi PDF:
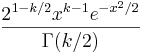
Transformations
- TBD
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:
