Formulas
From Socr
(Difference between revisions)
(→Transformations) |
(→Transformations) |
||
| Line 16: | Line 16: | ||
* [[AP_Statistics_Curriculum_2007_Normal_Prob | Standard Normal to General Normal Transformation]]: <math>\mu+\sigma\times X</math> | * [[AP_Statistics_Curriculum_2007_Normal_Prob | Standard Normal to General Normal Transformation]]: <math>\mu+\sigma\times X</math> | ||
* [[AP_Statistics_Curriculum_2007_Normal_Prob | General Normal to Standard Normal Transformation]]: <math>X-\mu \over \sigma</math> | * [[AP_Statistics_Curriculum_2007_Normal_Prob | General Normal to Standard Normal Transformation]]: <math>X-\mu \over \sigma</math> | ||
| - | * [http://en.wikipedia.org/wiki/Normal_distribution Standard Normal to Chi Transformation | + | * [http://en.wikipedia.org/wiki/Normal_distribution Standard Normal to Chi Transformation]: <math>|\ X |</math> |
| + | * [http://en.wikipedia.org/wiki/Normal_distribution Standard Normal to Chi-Square Transformation]: <math>\sum_{k=1}^{\nu} X_k^2</math> | ||
Revision as of 20:24, 24 April 2008
This SOCR Wiki page contains a number of formulas, mathematical expressions and symbolic representations that are used in varieties of SOCR resources. Usage is defined as a reference by image, text, TeX, URL, etc. For instance the SOCR Distributome project uses these formulas to represent PDFs, CDFs, transformations, etc.
Probability Density Functions (PDFs)
- Standard Normal PDF:
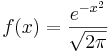
- General Normal PDF:
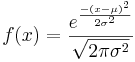
- Chi-Square PDF:
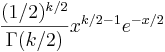
- Gamma PDF:
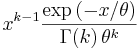
- Beta PDF:
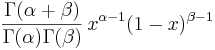
- Student's T PDF:
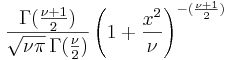
- Poisson PDF:
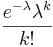
- Chi PDF:
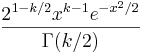
- Cauchy PDF:
![\frac{1}{\pi\gamma \left[1 + \left(\frac{x-x_0}{\gamma}\right)^2\right]}](/socr/uploads/math/a/9/2/a9260c6814d86ac3231f3934db752577.png)
Transformations
- Standard Normal to General Normal Transformation:
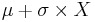
- General Normal to Standard Normal Transformation:
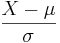
- Standard Normal to Chi Transformation:
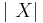
- Standard Normal to Chi-Square Transformation:
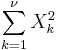
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:
