Formulas
From Socr
(Difference between revisions)
m (→Transformations) |
(→Probability Density Functions (PDFs): added Multinomial) |
||
| Line 17: | Line 17: | ||
\mbox{0 otherwise} \end{cases} </math> | \mbox{0 otherwise} \end{cases} </math> | ||
* [http://socr.ucla.edu/htmls/dist/Binomial_Distribution.html Binomial] PMF: <math> \begin{pmatrix} n \\ k \end{pmatrix} p^k (1-p)^{n-k}</math> | * [http://socr.ucla.edu/htmls/dist/Binomial_Distribution.html Binomial] PMF: <math> \begin{pmatrix} n \\ k \end{pmatrix} p^k (1-p)^{n-k}</math> | ||
| + | * [http://socr.ucla.edu/htmls/dist/Multinomiall_Distribution.html Multinomial] PMF: <math>f(x_1, x_2, \cdots, x_k)={n\choose x_1,x_2,\cdots, x_k}p_1^{x_1}p_2^{x_2}\cdots p_k^{x_k}</math>, where <math>\forall x_1+x_2+\cdots+x_k=n</math>, and <math>\forall p_1+p_2+\cdots+p_k=1</math>. | ||
* [http://socr.ucla.edu/htmls/dist/NegativeBinomial_Distribution.html Negative Binomial] PMF: <math> \begin{pmatrix} k + r - 1 \\ k \end{pmatrix} p^r(1-p)^k </math> | * [http://socr.ucla.edu/htmls/dist/NegativeBinomial_Distribution.html Negative Binomial] PMF: <math> \begin{pmatrix} k + r - 1 \\ k \end{pmatrix} p^r(1-p)^k </math> | ||
* [http://socr.ucla.edu/htmls/dist/Geometric_Distribution.html Geometric] PMF: <math> \begin{pmatrix} 1-p \end{pmatrix} ^{k-1}p </math> | * [http://socr.ucla.edu/htmls/dist/Geometric_Distribution.html Geometric] PMF: <math> \begin{pmatrix} 1-p \end{pmatrix} ^{k-1}p </math> | ||
Revision as of 22:24, 23 October 2009
Probability Density Functions (PDFs)
- Standard Normal PDF:
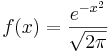
- General Normal PDF:
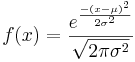
- Chi-Square PDF:
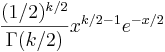
- Gamma PDF:
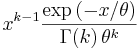
- Beta PDF:
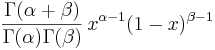
- Student's T PDF:
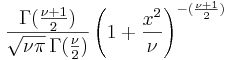
- Poisson PDF:
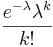
- Chi PDF:
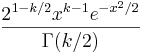
- Cauchy PDF:
![\frac{1}{\pi\gamma \left[1 + \left(\frac{x-x_0}{\gamma}\right)^2\right]}](/socr/uploads/math/a/9/2/a9260c6814d86ac3231f3934db752577.png)
- Exponential PDF:
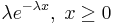
- F Distribution PDF:
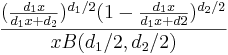
- Bernoulli PMF:
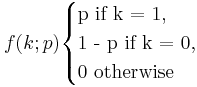
- Binomial PMF:
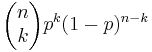
- Multinomial PMF:
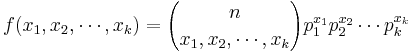 , where
, where  , and
, and 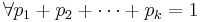 .
.
- Negative Binomial PMF:
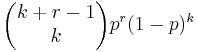
- Geometric PMF:
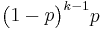
- Erlang PDF:
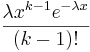
- Laplace PDF:
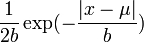
- Continuous Uniform PDF:
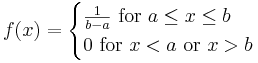
- Discrete Uniform PMF:
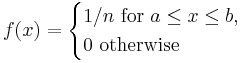
- Logarithmic PDF:
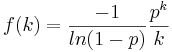
- Logistic PDF:
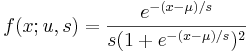
- Logistic-Exponential PDF:
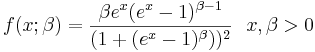
- Power Function PDF:
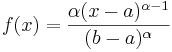
- Benford's Law:
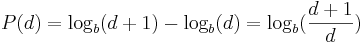
- Pareto PDF:
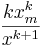
- Non-Central Student T PDF:
![f(t)=\frac{\nu^{\nu/2}e^{-\nu\mu^2/2(t^2+\nu)}} {\sqrt{\pi}\Gamma(\nu/2)2^{(\nu-1)/2}(t^2+\nu)^{(\nu+1)/2}} \times\int\limits_0^\infty x^\nu\exp\left[-\frac{1}{2}\left(x-\frac{\mu t}{\sqrt{t^2+\nu}}\right)^2\right]dx](/socr/uploads/math/e/3/7/e37a9ea8dea4ca3d0d7d55f76aaa430b.png)
- ArcSine PDF:
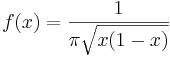
- Circle PDF:
![f(x)={2\sqrt{r^2 - x^2}\over \pi r^2 }, \forall x \in [-r , r]](/socr/uploads/math/4/5/a/45a7876ef35972bf28385be926c52b62.png)
- U-Quadratic PDF:
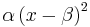
- Standard Uniform PDF:
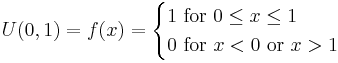
- Zipf:
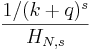
- Inverse Gamma:
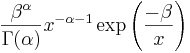
- Fisher-Tippett:
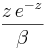
where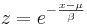
- Gumbel:
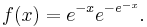
- HyperGeometric:
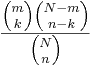
- Log-Normal:
![\frac{1}{x\sigma\sqrt{2\pi}}\exp\left[-\frac{\left(\ln(x)-\mu\right)^2}{2\sigma^2}\right]](/socr/uploads/math/b/3/f/b3f2a95779f28c24a5a265ba6498ceec.png)
- Gilbrats:
![\frac{1}{\sigma\sqrt{2\pi}}\exp\left[-\frac{\left(\ln(x)\right)^2}{2\sigma^2}\right]](/socr/uploads/math/d/0/3/d03d955b51d917ba307deef3c7e277a0.png)
- Hyperbolic Secant:
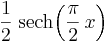
- Gompertz:
![b e^{-bx} e^{-\eta e^{-bx}}\left[1 + \eta\left(1 - e^{-bx}\right)\right]](/socr/uploads/math/4/e/f/4efe11d1016f67a67761bf1697fb5a9b.png)
- Standard Cauchy:
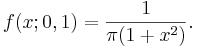
Transformations
- Standard Normal to General Normal Transformation:
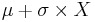
- General Normal to Standard Normal Transformation:
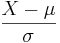
- Standard Normal to Chi Transformation:
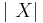
- Standard Normal to Chi-Square Transformation:
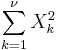
- Gamma to General Normal Transformation:
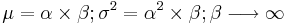
- Gamma to Exponential Transformation: The special case of
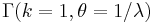 is equivalent to exponential Exp(λ).
is equivalent to exponential Exp(λ).
- Gamma to Beta Transformation:
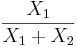 .
.
- Student's T to Standard Normal Transformation:
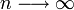
- Student's T to Cauchy Transformation:
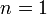
- Cauchy to General Cauchy Transformation:
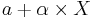
- General Cauchy to Cauchy Transformation:
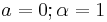
- Fisher's F to Student's T:
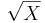
- Student's T to Fisher's F: X2
- Bernoulli to Binomial Transformation:
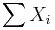 (iid)
(iid)
- Binomial to Bernoulli Transformation:
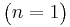
- Binomial to General Normal Transformation:
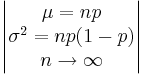
- Binomial to Poisson Transformation:
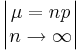
- Negative Binomial to Geometric Transformation:
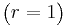
- Erlang to Exponential Transformation:
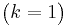
- Erlang to Chi-Square Transformation:
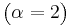
- Laplace to Exponential Transformation:
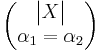
- Exponential to Laplace Transformation:

- Beta to Arcsine Transformation:
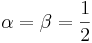
- Noncentral Student's T to Normal Transformation:
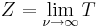
- Noncentral Student's T to Student's T Transformation:
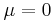
- Standard Uniform to Pareto Transformation:
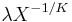
- Standard Uniform to Benford Transformation:
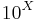
- Standard Uniform to Exponential Transformation:
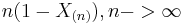
- Standard Uniform to Log Logistic Transformation:
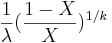
- Standard Uniform to Standard Triangular Transformation: X1 − X2
- Standard Uniform to Logistic Exponential Transformation:
![\frac{log[1+(\frac{X}{1-X})^{1/K}]}{\lambda}](/socr/uploads/math/b/b/1/bb14e96da3be11b8bee63fcfbb54fefa.png)
- Standard Uniform to Beta Transformation: If X has a standard uniform distribution,
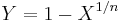 has a beta distribution
has a beta distribution
- Beta to Standard Uniform Transformation: β = γ = 1
- Continuous Uniform to Standard Uniform Transformation:
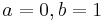
- Pareto to Exponential:
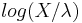
- Logistic Exponential to Exponential:
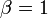
- Zipf to Discrete Uniform:
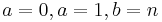
- Discrete Uniform to Rectangular:
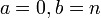
- Poisson to Normal:
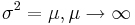
- Binomial to Poisson:
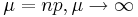
- Gamma to Inverted Gamma:
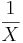
- Fisher-Tippett to Gumbel:
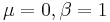
- Hypergeometric to Binomial:
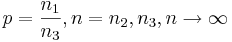
- Log-Normal to Normal:
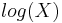
- Normal to Log-Normal:
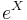
- Log-Normal to Gibrat's:
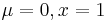
- Cauchy to Standard Cauchy:
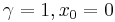
- Standard Cauchy to Cauchy:
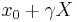
- Standard Cauchy to Hyperbolic Secant:
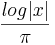
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:
