SOCR Activity ANOVA FlignerKilleen MeatConsumption
From Socr
| Line 162: | Line 162: | ||
==[[AP_Statistics_Curriculum_2007_EDA_Pics|Exploratory data analyses (EDA)]]== | ==[[AP_Statistics_Curriculum_2007_EDA_Pics|Exploratory data analyses (EDA)]]== | ||
| - | + | In the following analysis, we will aim to perform an analysis of variance (ANOVA) to compare the meat consumption amounts between different countries and/or across time. Note that the data points for each country-meat type combination are from the various years. Typically, we would expect the amount not to change between the years (especially in this 7-year timespan). Even if it did, in assuming homoscedasticity, we are making the assumption that any increase or decrease is constant between countries. Applying the Fligner-Killeen test will help us decide if this assumption is valid. | |
| + | Look at the bar graphs listed below and note which of them seem to vary more than the others between the years. | ||
| - | <center>[[Image: | + | <center>[[Image:SOCR_Activity_ANOVA_FlignerKilleen_MeatConsumption_Fig2.png|500px]]</center> |
| + | <center>[[Image:SOCR_Activity_ANOVA_FlignerKilleen_MeatConsumption_Fig3.png|500px]]</center> | ||
| + | <center>[[Image:SOCR_Activity_ANOVA_FlignerKilleen_MeatConsumption_Fig4.png|500px]]</center> | ||
| + | <center>[[Image:SOCR_Activity_ANOVA_FlignerKilleen_MeatConsumption_Fig5.png|500px]]</center> | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
==Quantitative data analysis (QDA)== | ==Quantitative data analysis (QDA)== | ||
Revision as of 22:41, 21 February 2013
SOCR Educational Materials - Activities - SOCR Meat Consumption Activity – ANOVA assumptions about the variance homogeneity Activity
Motivation and Goals
In many developed countries, when people imagine their next meal, they focus on one specific part: the meat. That choice of meat, however, varies from country to country due to the popularity and availability of various domesticated animals. Furthermore, the amount of meat eaten has a surprising degree of variability across time, cultures and geographic regions.
The following activity will study the effects of that variance on the statistical analyses. Specifically, we will consider how deviations from homoscedasticity (also known as equivalence of variance or variance homogeneity) can lead to making some incomplete or even incorrect conclusions. To do so, we will employ the Fligner-Killeen method to analyze some real meet consumption data.
Summary
This activity uses a reduced version of the open-source meat-consumption dataset. All data comes from the US Census Bureau.
This dataset summarizes the meat consumption, by animal type, of various countries (the European Union (EU) is being treated as a single country in this case). For simplicity, records from countries that did provide consumption measures for all meat types and all years were removed from the data set.
Data
Data Description
- Number of cases: 147
- Variables
- Country: The country or world region in question
- Brazil
- China
- European Union
- Japan
- Mexico
- Russia
- United States
- Meat: The type of meat
- Beef
- Pork
- Poultry
- Years Represented (2000 – 2006)
- Country: The country or world region in question
- Values are in thousands of metric tons
Data Summaries
Chicken/Poultry
| Year | Brazil | China | Europe | Japan | Mexico | Russia | UnitedStates | YearAverage | YearSD |
|---|---|---|---|---|---|---|---|---|---|
| 2000 | 5110 | 9393 | 6934 | 1772 | 2163 | 1320 | 11474 | 5452.286 | 3990.459 |
| 2001 | 5341 | 9237 | 7359 | 1797 | 2311 | 1588 | 11558 | 5598.714 | 3942.57 |
| 2002 | 5873 | 9556 | 7417 | 1830 | 2424 | 1697 | 12270 | 5866.714 | 4134.211 |
| 2003 | 5742 | 9963 | 7312 | 1841 | 2627 | 1680 | 12540 | 5957.857 | 4234.565 |
| 2004 | 5992 | 9931 | 7280 | 1713 | 2713 | 1675 | 13080 | 6054.857 | 4379.591 |
| 2005 | 6612 | 10088 | 7596 | 1880 | 2871 | 2139 | 13430 | 6373.714 | 4388.111 |
| 2006 | 6853 | 10371 | 7380 | 1908 | 3005 | 2382 | 13754 | 6521.857 | 4448.974 |
| Country_Average | 5931.857 | 9791.286 | 7325.429 | 1820.143 | 2587.714 | 1783 | 12586.57 | ||
| Country_SD | 629.6543 | 407.0908 | 200.4826 | 66.03895 | 304.2404 | 357.6777 | 886.5564 |
Pork
| Year | Brazil | China | Europe | Japan | Mexico | Russia | UnitedStates | YearAverage | YearSD |
|---|---|---|---|---|---|---|---|---|---|
| 2000 | 1827 | 40378 | 19242 | 2228 | 1252 | 2019 | 8455 | 10771.57 | 14570.99 |
| 2001 | 1919 | 41829 | 19317 | 2268 | 1298 | 2076 | 8389 | 11013.71 | 15049.33 |
| 2002 | 1975 | 43238 | 19746 | 2377 | 1349 | 2453 | 8685 | 11403.29 | 15502.7 |
| 2003 | 1957 | 45054 | 20043 | 2373 | 1423 | 2420 | 8816 | 11726.57 | 16145.49 |
| 2004 | 1979 | 46648 | 19773 | 2562 | 1556 | 2337 | 8817 | 11953.14 | 16648.16 |
| 2005 | 1949 | 49703 | 19768 | 2507 | 1556 | 2476 | 8669 | 12375.43 | 17714.83 |
| 2006 | 2191 | 51809 | 20015 | 2450 | 1580 | 2637 | 8640 | 12760.29 | 18438.64 |
| Country_Average | 1971 | 45522.71 | 19700.57 | 2395 | 1430.571 | 2345.429 | 8638.714 | ||
| Country_SD | 110 | 4159.521 | 312.355 | 121.3013 | 135.3808 | 223.0148 | 164.5121 |
Beef
| Year | Brazil | China | Europe | Japan | Mexico | Russia | UnitedStates | YearAverage | YearSD |
|---|---|---|---|---|---|---|---|---|---|
| 2000 | 6102 | 5284 | 8106 | 1585 | 2309 | 2246 | 12502 | 5447.714 | 3922.316 |
| 2001 | 6191 | 5434 | 7658 | 1419 | 2341 | 2400 | 12351 | 5399.143 | 3835.093 |
| 2002 | 6437 | 5818 | 8187 | 1319 | 2409 | 2450 | 12737 | 5622.429 | 4016.753 |
| 2003 | 6273 | 6274 | 8315 | 1366 | 2308 | 2378 | 12340 | 5607.714 | 3933.847 |
| 2004 | 6400 | 6703 | 8292 | 1182 | 2368 | 2308 | 12667 | 5702.857 | 4077.861 |
| 2005 | 6774 | 7026 | 8194 | 1200 | 2419 | 2503 | 12663 | 5825.571 | 4056.693 |
| 2006 | 6939 | 7395 | 8270 | 1173 | 2509 | 2370 | 12830 | 5926.571 | 4148.408 |
| Country_Average | 6445.143 | 6276.286 | 8146 | 1320.571 | 2380.429 | 2379.286 | 12584.29 | ||
| Country_SD | 307.1685 | 806.2036 | 226.9295 | 151.2138 | 71.75388 | 85.31259 | 190.4396 |
Raw Dataset
| Country | Meat | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 |
|---|---|---|---|---|---|---|---|---|
| Brazil | Beef | 6102 | 6191 | 6437 | 6273 | 6400 | 6774 | 6939 |
| Brazil | Pork | 1827 | 1919 | 1975 | 1957 | 1979 | 1949 | 2191 |
| Brazil | Poultry | 5110 | 5341 | 5873 | 5742 | 5992 | 6612 | 6853 |
| China | Beef | 5284 | 5434 | 5818 | 6274 | 6703 | 7026 | 7395 |
| China | Pork | 40378 | 41829 | 43238 | 45054 | 46648 | 49703 | 51809 |
| China | Poultry | 9393 | 9237 | 9556 | 9963 | 9931 | 10088 | 10371 |
| EuropeanUnion | Beef | 8106 | 7658 | 8187 | 8315 | 8292 | 8194 | 8270 |
| EuropeanUnion | Pork | 19242 | 19317 | 19746 | 20043 | 19773 | 19768 | 20015 |
| EuropeanUnion | Poultry | 6934 | 7359 | 7417 | 7312 | 7280 | 7596 | 7380 |
| Japan | Beef | 1585 | 1419 | 1319 | 1366 | 1182 | 1200 | 1173 |
| Japan | Pork | 2228 | 2268 | 2377 | 2373 | 2562 | 2507 | 2450 |
| Japan | Poultry | 1772 | 1797 | 1830 | 1841 | 1713 | 1880 | 1908 |
| Mexico | Beef | 2309 | 2341 | 2409 | 2308 | 2368 | 2419 | 2509 |
| Mexico | Pork | 1252 | 1298 | 1349 | 1423 | 1556 | 1556 | 1580 |
| Mexico | Poultry | 2163 | 2311 | 2424 | 2627 | 2713 | 2871 | 3005 |
| Russia | Beef | 2246 | 2400 | 2450 | 2378 | 2308 | 2503 | 2370 |
| Russia | Pork | 2019 | 2076 | 2453 | 2420 | 2337 | 2476 | 2637 |
| Russia | Poultry | 1320 | 1588 | 1697 | 1680 | 1675 | 2139 | 2382 |
| UnitedStates | Beef | 12502 | 12351 | 12737 | 12340 | 12667 | 12663 | 12830 |
| UnitedStates | Pork | 8455 | 8389 | 8685 | 8816 | 8817 | 8669 | 8640 |
| UnitedStates | Poultry | 11474 | 11558 | 12270 | 12540 | 13080 | 13430 | 13754 |
Exploratory data analyses (EDA)
In the following analysis, we will aim to perform an analysis of variance (ANOVA) to compare the meat consumption amounts between different countries and/or across time. Note that the data points for each country-meat type combination are from the various years. Typically, we would expect the amount not to change between the years (especially in this 7-year timespan). Even if it did, in assuming homoscedasticity, we are making the assumption that any increase or decrease is constant between countries. Applying the Fligner-Killeen test will help us decide if this assumption is valid. Look at the bar graphs listed below and note which of them seem to vary more than the others between the years.
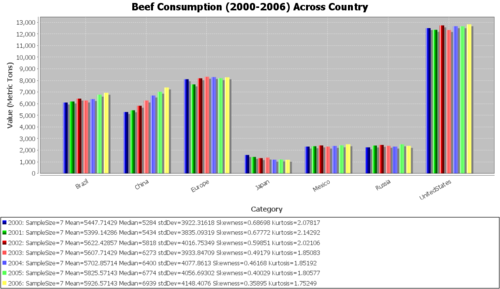
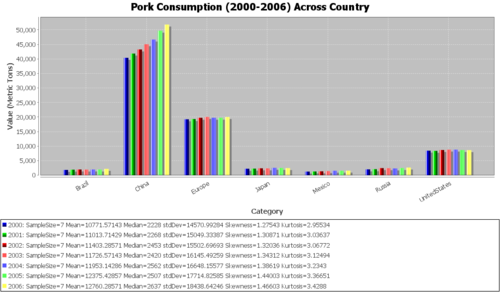
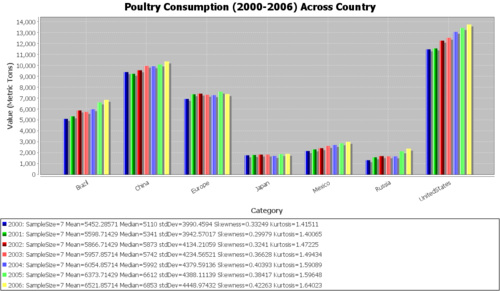
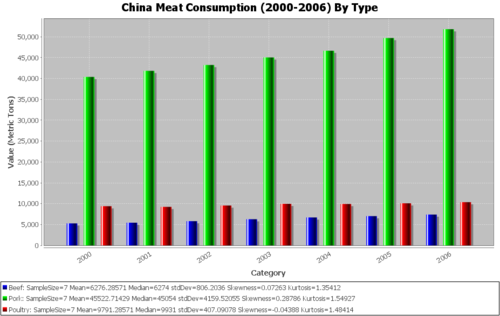
Quantitative data analysis (QDA)
Open the SOCR ANOVA-Two Way applet (requires Java-enabled browser).
Copy and paste the Sex and Locality data into the first two columns. Pick one of the other six variables (in this case, Shell.h) and copy that data into the third. Use the ctrl + c command and the "paste" button in the applet. Name the three columns appropriately.
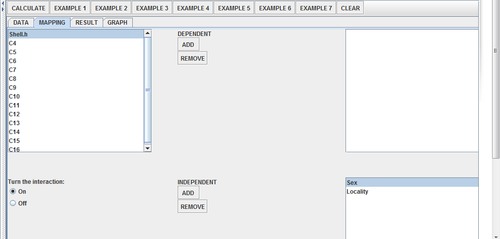
Next, click on the “mapping tab”. Select "sex" and "locality" as the independent variables. Next, name the third column as your dependent variable. We will use "shell.h" in the following example, but it is recommended that you use another in its place to explore these measures. Make sure you click “turn the interaction” on,
Press the Calculate button. This should bring up the results page with the following text:
- ANOVA results
- Sample Size = 112
- Dependent Variable = Shell.h
- Independent Variable(s) = Locality Sex Interaction Locality: Sex
- *** Two-Way Analysis of Variance Results ***
- See EBook's Standard 2-Way ANOVA Table
| Variance Source | DF | RSS | MSS | F-Statistics | P-value |
|---|---|---|---|---|---|
| Main Effect: Locality | 2 | 1912452.01667 | 956226.00833 | 18.39651 | 0.00000 |
| Main Effect: Sex | 1 | 6197835.01312 | 6197835.01312 | 119.23809 | 0.00000 |
| Interaction Locality: Sex | 2 | 161192.25392 | 80596.12696 | 1.55056 | 0.21690 |
| Error | 106 | 5509737.01359 | 51978.65107 | ||
| Total: | 111 | 13170123.10714 |
- Variable: Locality
- Degrees of Freedom = 2
- Residual Sum of Squares = 1912452.01667
- Mean Square Error = 956226.00833
- F-Value = 18.39651
- P-Value = .00000
- Variable: Sex
- Degrees of Freedom = 1
- Residual Sum of Squares = 6197835.01312
- Mean Square Error = 6197835.01312
- F-Value = 119.23809
- P-Value = .00000
- Variable: Interaction Locality: Sex
- Degrees of Freedom = 2
- Residual Sum of Squares = 161192.25392
- Mean Square Error = 80596.12696
- F-Value = 1.55056
- P-Value = .21690
- Residual: Degrees of Freedom = 106
- Residual Sum of Squares = 5509737.01359
- Mean Square Error = 51978.65107
- F-Value = 29.47512
- P-Value = 0.0
- R-Square = .60598
For the effect of locality and the interaction effects, you can need to conduct post-hoc t-tests, in this case, a pooled independent samples t-test. You can do this in a similar manner to the two-way ANOVA; however will have to enter the values in a slightly different way (see below). Note that your critical t-values must have Bonferoni correction.
Conclusions
According to the results of the analysis, you will find that there is are significant main effects of locality (F(2, 106) = 18.39651, p < 0.001) and sex (F(1, 106) = 119.23809, p < 0.001) on shell width. The interaction between sex and locality is not significant on shell width (F (2,106) = 1.55056, p > 0.20). Post-hoc tests reveal that t-tests will reveal that there is a significant difference in width between male (M 7106.88136, SD = 247.06778) and female (M = 7578.03773, SD = 256.89806) snails shells (t (110) = 9.88846, p < 0.001). The 99.7% confidence interval for the difference is 471.15638 ± 157.08993. Note that this interval does not include 0 (a lack of difference between the means). There is also a significant difference in width between the snails collected at localities one and two, two and three, & one and three. We leave these analyses to you in the first practice problems
Based on these results, it would be possible to classify whether a Cocholotoma septemspirale is male or female, regardless of the locality it comes from (there is no interaction of the two effects); females have significantly taller shells. Limitations of the study include its correlational nature. One issue with the study, for example, is that age might be a confounding variable, if these snails are the type that grows throughout their lifecycle.
Practice problems
- Finish the post-hoc t-tests for the effect of locality on shell width.
- Complete an analysis similar to the one above, using one of the variables other than shell.h as -your dependent variable. See if that variable would be of use in classifying the snails.
- Complete a new analysis of this pain/neuroimaging data set. Use sex and disease group as independent variables. Choose for your dependent variable one of the brain volumes.
See also
References
- Che, Annie, Cui, Jenny, and Dinov, Ivo (2009). SOCR Analyses: Implementation and Demonstration of a New Graphical Statistics Educational Toolkit. JSS, Vol. 30, Issue 3, Apr 2009.
- Che, A, Cui, J, and Dinov, ID (2009) SOCR Analyses – an Instructional Java Web-based Statistical Analysis Toolkit, JOLT, 5(1), 1-19, March 2009.
- Dinov, ID. Statistics Online Computational Resource, Journal of Statistical Software, Vol. 16, No. 1, 1-16, October 2006.
- Reichenbach F, Baur H, Neubert E (2012) Sexual dimorphism in shells of Cochlostoma septemspirale (Caenogastropoda, Cyclophoroidea, Diplommatinidae, Cochlostomatinae). ZooKeys 208: 1-16. doi:10.3897/zookeys.208.2869
- Baur H, Reichenbach F, Neubert E (2012) Data from: Sexual dimorphism in shells of Cochlostoma septemspirale (Caenogastropoda, Cyclophoroidea, Diplommatinidae, Cochlostomatinae). Dryad Digital Repository. doi:10.5061/dryad.ns7v7
Translate this page:
