SOCR Activity ANOVA SnailsSexualDimorphism
From Socr
(→Quantitative data analysis (QDA)) |
(→Quantitative data analysis (QDA)) |
||
| Line 292: | Line 292: | ||
: [[AP_Statistics_Curriculum_2007_ANOVA_2Way| See EBook's Standard 2-Way ANOVA Table]] | : [[AP_Statistics_Curriculum_2007_ANOVA_2Way| See EBook's Standard 2-Way ANOVA Table]] | ||
| + | <center> | ||
{| class="wikitable" style="text-align:center; width:30%" border="1" | {| class="wikitable" style="text-align:center; width:30%" border="1" | ||
|- | |- | ||
| Line 306: | Line 307: | ||
|Total:||111||13170123.10714|| || || | |Total:||111||13170123.10714|| || || | ||
|} | |} | ||
| + | </center> | ||
:Variable: Locality | :Variable: Locality | ||
Revision as of 00:01, 29 November 2012
Contents |
SOCR Educational Materials - Activities - SOCR ANOVA: Snails Sexual Dimorphism Activity
Many natural processes are observed directly or indirectly via recording quantitative measurements (e.g., height, length, time, size, etc.) These observations (or data) may have additional meta-data that describe the units, objects or subjects that we measure (e.g., gender, race, type, taxa, species, etc.)
Motivation and Goals
When there are diverse types of qualitative and quantitative measurements that can be observed about the process, how can we make scientifically valid and robust inference of the data? This activity deals with the situation of a two-way analysis of variance (ANOVA). You will learn how to use the SOCR tools to deal with data that involves multiple variables.
Summary
This activity will recreate part of the design of a classification method for the Cocholotoma septemspirale snail. By observing multiple traits of the shells, the original researchers were able to decide on a series of dimorphisms (difference in forms) between male and female snails.
The data set below is a reduced version of the Sexual Dimorphism in Snails dataset.
Data Description
- Number of cases: 112
- Variable Names:
- Sex: Sex of the snail; 1 = female, 2 = male
- Location: Where the snail was found in Switzerland; 1 = Chasseral, 2 = Orvine, 3 = Combes de Nods
- shell.h: Height of the shell, in micrometers
- shell.w: Width of the shell, in micrometers
- aperture.h: Height of the shell aperture (where the snail comes out of), in micrometers
- aperture.w: Height of the shell aperture, in micrometers
- whorl.w: Width of the last whorl (spiral section) on the shell, in micrometers.
- rib.n: Number of ribs on the last whorl on the shell, in micrometers.
Dataset
| Sex | locality | shell.h | shell.w | aperture.h | aperture.w | whorl.w | rib.n |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 7063 | 3860 | 2564 | 2522 | 3119 | 29 |
| 1 | 1 | 7535 | 3846 | 2522 | 2629 | 3332 | 37 |
| 1 | 1 | 7484 | 3952 | 2680 | 2541 | 3258 | 34 |
| 1 | 1 | 7516 | 3763 | 2671 | 2703 | 3217 | 31 |
| 1 | 1 | 7211 | 3698 | 2555 | 2541 | 3133 | 30 |
| 1 | 1 | 7526 | 3828 | 2573 | 2555 | 3143 | 28 |
| 1 | 1 | 7576 | 3851 | 2439 | 2504 | 3207 | 32 |
| 1 | 1 | 7558 | 3781 | 2471 | 2481 | 3143 | 35 |
| 1 | 1 | 7674 | 3828 | 2652 | 2513 | 3230 | 31 |
| 1 | 1 | 7526 | 3786 | 2439 | 2555 | 3166 | 29 |
| 1 | 1 | 7641 | 3943 | 2587 | 2481 | 3300 | 30 |
| 1 | 1 | 7470 | 4087 | 2712 | 2606 | 3286 | 33 |
| 1 | 1 | 7262 | 3693 | 2573 | 2504 | 3124 | 38 |
| 1 | 1 | 7410 | 3781 | 2532 | 2499 | 3152 | 28 |
| 1 | 1 | 7799 | 4045 | 2782 | 2666 | 3342 | 31 |
| 1 | 1 | 7567 | 3855 | 2583 | 2647 | 3226 | 33 |
| 1 | 1 | 7428 | 3952 | 2481 | 2546 | 3226 | 32 |
| 1 | 1 | 7368 | 3730 | 2448 | 2407 | 3119 | 33 |
| 1 | 1 | 6915 | 3615 | 2407 | 2259 | 3069 | 29 |
| 1 | 1 | 7327 | 3920 | 2587 | 2522 | 3217 | 36 |
| 1 | 1 | 7502 | 3837 | 2657 | 2536 | 3087 | 32 |
| 2 | 1 | 7188 | 4003 | 2629 | 2546 | 3277 | 31 |
| 2 | 1 | 7178 | 4119 | 2754 | 2670 | 3258 | 25 |
| 2 | 1 | 7192 | 3865 | 2587 | 2374 | 3101 | 27 |
| 2 | 1 | 7035 | 3971 | 2652 | 2647 | 3207 | 31 |
| 2 | 1 | 6674 | 3823 | 2532 | 2573 | 3004 | 30 |
| 2 | 1 | 7470 | 4027 | 2837 | 2694 | 3184 | 27 |
| 2 | 1 | 7252 | 3952 | 2629 | 2407 | 3166 | 27 |
| 2 | 1 | 6739 | 3855 | 2606 | 2439 | 3087 | 29 |
| 2 | 1 | 7345 | 3994 | 2721 | 2555 | 3166 | 31 |
| 2 | 1 | 7419 | 3869 | 2689 | 2564 | 3198 | 29 |
| 2 | 1 | 7040 | 3837 | 2513 | 2481 | 3124 | 33 |
| 2 | 1 | 6623 | 3920 | 2564 | 2564 | 3124 | 26 |
| 2 | 1 | 7169 | 3980 | 2828 | 2434 | 3161 | 30 |
| 2 | 1 | 6956 | 3777 | 2615 | 2495 | 3050 | 29 |
| 2 | 1 | 6549 | 3749 | 2471 | 2425 | 2994 | 25 |
| 2 | 1 | 6831 | 3763 | 2536 | 2407 | 3036 | 30 |
| 2 | 1 | 7053 | 3985 | 2805 | 2573 | 3184 | 32 |
| 2 | 1 | 6919 | 3837 | 2481 | 2448 | 3152 | 32 |
| 2 | 1 | 6808 | 3911 | 2666 | 2499 | 3101 | 33 |
| 2 | 1 | 7137 | 3573 | 2471 | 2522 | 3050 | 27 |
| 2 | 1 | 6928 | 3851 | 2587 | 2495 | 3166 | 28 |
| 1 | 2 | 7294 | 3679 | 2458 | 2356 | 3101 | 33 |
| 1 | 2 | 7576 | 3786 | 2721 | 2777 | 3143 | 31 |
| 1 | 2 | 7840 | 3892 | 2712 | 2471 | 3082 | 32 |
| 1 | 2 | 7586 | 3860 | 2573 | 2647 | 3207 | 31 |
| 1 | 2 | 7715 | 3860 | 2536 | 2546 | 3184 | 33 |
| 1 | 2 | 7715 | 4017 | 2777 | 2638 | 3305 | 35 |
| 1 | 2 | 7456 | 3929 | 2629 | 2680 | 3203 | 32 |
| 1 | 2 | 7526 | 3878 | 2583 | 2606 | 3291 | 35 |
| 1 | 2 | 7526 | 3772 | 2606 | 2564 | 3152 | 33 |
| 1 | 2 | 7780 | 3772 | 2735 | 2629 | 3217 | 31 |
| 1 | 2 | 7077 | 3703 | 2305 | 2337 | 3092 | 34 |
| 1 | 2 | 7336 | 3781 | 2555 | 2439 | 3143 | 36 |
| 1 | 2 | 7544 | 3855 | 2583 | 2638 | 3119 | 36 |
| 2 | 2 | 7086 | 4077 | 2772 | 2629 | 3143 | 31 |
| 2 | 2 | 6716 | 3846 | 2694 | 2689 | 3069 | 29 |
| 2 | 2 | 7276 | 3929 | 2587 | 2481 | 3170 | 32 |
| 2 | 2 | 6928 | 3860 | 2712 | 2564 | 3082 | 34 |
| 2 | 2 | 6716 | 3818 | 2689 | 2439 | 3082 | 34 |
| 2 | 2 | 6915 | 3869 | 2721 | 2388 | 3069 | 35 |
| 2 | 2 | 7095 | 3929 | 2712 | 2490 | 3110 | 32 |
| 2 | 2 | 6928 | 3952 | 2754 | 2638 | 3092 | 30 |
| 2 | 2 | 7387 | 3804 | 2592 | 2564 | 3110 | 31 |
| 2 | 2 | 7095 | 3869 | 2615 | 2541 | 3272 | 33 |
| 2 | 2 | 7095 | 3846 | 2638 | 2587 | 3119 | 28 |
| 2 | 2 | 6938 | 3846 | 2638 | 2638 | 3069 | 32 |
| 2 | 2 | 7169 | 3721 | 2745 | 2629 | 3092 | 29 |
| 2 | 2 | 7035 | 3689 | 2513 | 2397 | 3018 | 29 |
| 2 | 2 | 7086 | 3786 | 2596 | 2356 | 3101 | 31 |
| 2 | 2 | 7123 | 4059 | 2731 | 2819 | 3217 | 34 |
| 2 | 2 | 7137 | 3878 | 2684 | 2546 | 3133 | 35 |
| 2 | 2 | 6956 | 3619 | 2407 | 2296 | 3082 | 31 |
| 2 | 2 | 7123 | 3929 | 2550 | 2541 | 3124 | 34 |
| 2 | 2 | 7220 | 3869 | 2657 | 2448 | 3207 | 33 |
| 2 | 2 | 7493 | 3971 | 2680 | 2638 | 3235 | 30 |
| 2 | 2 | 7271 | 3994 | 2638 | 2620 | 3193 | 33 |
| 1 | 3 | 7831 | 3948 | 2647 | 2708 | 3360 | 33 |
| 1 | 3 | 7863 | 4207 | 2712 | 2694 | 3416 | 30 |
| 1 | 3 | 7775 | 3952 | 2721 | 2573 | 3291 | 32 |
| 1 | 3 | 7715 | 4068 | 2689 | 2430 | 3300 | 29 |
| 1 | 3 | 7493 | 3892 | 2731 | 2578 | 3175 | 33 |
| 1 | 3 | 7243 | 4008 | 2689 | 2786 | 3110 | 32 |
| 1 | 3 | 8187 | 4207 | 2953 | 2902 | 3490 | 33 |
| 1 | 3 | 7850 | 4119 | 2721 | 2680 | 3499 | 35 |
| 1 | 3 | 8086 | 4128 | 2819 | 2680 | 3291 | 34 |
| 1 | 3 | 8211 | 3906 | 2647 | 2541 | 3277 | 31 |
| 1 | 3 | 7799 | 3929 | 2564 | 2499 | 3351 | 30 |
| 1 | 3 | 7683 | 3962 | 2721 | 2666 | 3272 | 31 |
| 1 | 3 | 7428 | 3952 | 2541 | 2527 | 3258 | 34 |
| 1 | 3 | 7715 | 3994 | 2754 | 2657 | 3291 | 36 |
| 1 | 3 | 7780 | 3994 | 2647 | 2680 | 3383 | 33 |
| 1 | 3 | 7567 | 3869 | 2583 | 2365 | 3249 | 34 |
| 1 | 3 | 7891 | 3943 | 2573 | 2564 | 3207 | 26 |
| 1 | 3 | 7526 | 3804 | 2638 | 2522 | 3217 | 32 |
| 1 | 3 | 7664 | 3888 | 2555 | 2541 | 3249 | 33 |
| 2 | 3 | 7003 | 3962 | 2564 | 2439 | 3268 | 34 |
| 2 | 3 | 7368 | 4077 | 2860 | 2712 | 3156 | 36 |
| 2 | 3 | 7276 | 3837 | 2504 | 2300 | 3143 | 30 |
| 2 | 3 | 7276 | 3814 | 2546 | 2374 | 3161 | 32 |
| 2 | 3 | 6989 | 3633 | 2189 | 2161 | 3277 | 35 |
| 2 | 3 | 7104 | 3814 | 2763 | 2680 | 3087 | 36 |
| 2 | 3 | 7123 | 3971 | 2721 | 2564 | 3217 | 32 |
| 2 | 3 | 7229 | 3855 | 2439 | 2388 | 3281 | 31 |
| 2 | 3 | 7396 | 4119 | 2596 | 2661 | 3268 | 30 |
| 2 | 3 | 7660 | 3721 | 2680 | 2458 | 3198 | 36 |
| 2 | 3 | 7044 | 3892 | 2735 | 2546 | 3036 | 34 |
| 2 | 3 | 7220 | 3772 | 2647 | 2416 | 3087 | 29 |
| 2 | 3 | 7317 | 4119 | 2911 | 2869 | 3235 | 32 |
| 2 | 3 | 6841 | 3962 | 2763 | 2703 | 3152 | 35 |
| 2 | 3 | 7294 | 4054 | 2754 | 2416 | 3166 | 32 |
| 2 | 3 | 7873 | 4193 | 2920 | 2893 | 3342 | 30 |
Exploratory data analyses (EDA)
Various data patterns may be observed and explored using different types of graphical tools for plotting variables. Which of the following graphs are more or less likely to demonstrate visually significant grouping differences?
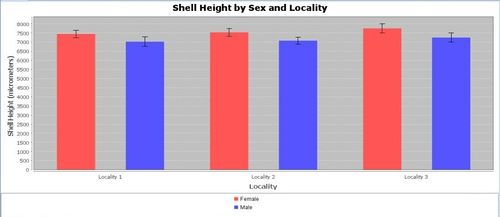
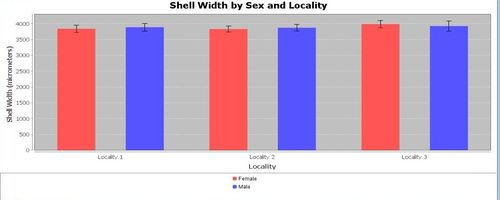
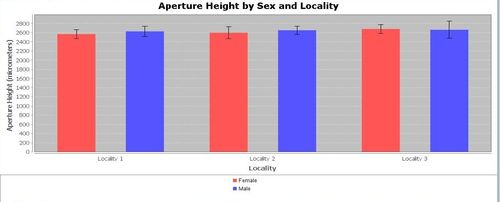
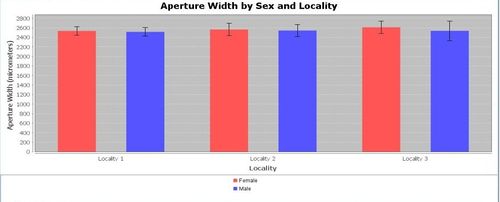
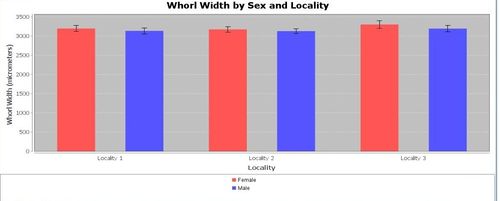
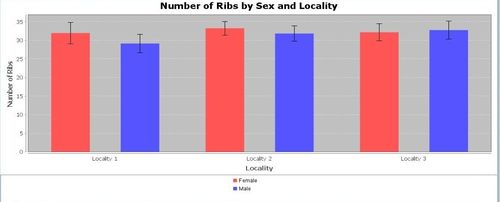
Quantitative data analysis (QDA)
Open the SOCR ANOVA-Two Way applet (requires Java-enabled browser).
Copy and paste the Sex and Locality data into the first two columns. Pick one of the other six variables (in this case, Shell.h) and copy that data into the third. Use the ctrl + c command and the "paste" button in the applet. Name the three columns appropriately.
Next, click on the “mapping tab”. Select "sex" and "locality" as the independent variables. Next, name the third column as your dependent variable. We will use "shell.h" in the following example, but it is recommended that you use another in its place to explore these measures. Make sure you click “turn the interaction” on,
Press the Calculate button. This should bring up the results page with the following text:
- ANOVA results
- Sample Size = 112
- Dependent Variable = Shell.h
- Independent Variable(s) = Locality Sex Interaction Locality: Sex
- *** Two-Way Analysis of Variance Results ***
- See EBook's Standard 2-Way ANOVA Table
| Variance Source | DF | RSS | MSS | F-Statistics | P-value |
|---|---|---|---|---|---|
| Main Effect: Locality | 2 | 1912452.01667 | 956226.00833 | 18.39651 | 0.00000 |
| Main Effect: Sex | 1 | 6197835.01312 | 6197835.01312 | 119.23809 | 0.00000 |
| Interaction Locality: Sex | 2 | 161192.25392 | 80596.12696 | 1.55056 | 0.21690 |
| Error | 106 | 5509737.01359 | 51978.65107 | ||
| Total: | 111 | 13170123.10714 |
- Variable: Locality
- Degrees of Freedom = 2
- Residual Sum of Squares = 1912452.01667
- Mean Square Error = 956226.00833
- F-Value = 18.39651
- P-Value = .00000
- Variable: Sex
- Degrees of Freedom = 1
- Residual Sum of Squares = 6197835.01312
- Mean Square Error = 6197835.01312
- F-Value = 119.23809
- P-Value = .00000
- Variable: Interaction Locality: Sex
- Degrees of Freedom = 2
- Residual Sum of Squares = 161192.25392
- Mean Square Error = 80596.12696
- F-Value = 1.55056
- P-Value = .21690
- Residual: Degrees of Freedom = 106
- Residual Sum of Squares = 5509737.01359
- Mean Square Error = 51978.65107
- F-Value = 29.47512
- P-Value = 0.0
- R-Square = .60598
For the effect of locality and the interaction effects, you can need to conduct post-hoc t-tests, in this case, a pooled independent samples t-test. You can do this in a similar manner to the two-way ANOVA; however will have to enter the values in a slightly different way (see below). Note that your critical t-values must have Bonferoni correction.
Conclusions
According to the results of the analysis, you will find that there is are significant main effects of locality (F(2, 106) = 18.39651, p < 0.001) and sex (F(1, 106) = 119.23809, p < 0.001) on shell width. The interaction between sex and locality is not significant on shell width (F (2,106) = 1.55056, p > 0.20). Post-hoc tests reveal that t-tests will reveal that there is a significant difference in width between male (M 7106.88136, SD = 247.06778) and female (M = 7578.03773, SD = 256.89806) snails shells (t (110) = 9.88846, p < 0.001). The 99.7% confidence interval for the difference is 471.15638 ± 157.08993. Note that this interval does not include 0 (a lack of difference between the means). There is also a significant difference in width between the snails collected at localities one and two, two and three, & one and three. We leave these analyses to you in the first practice problems
Based on these results, it would be possible to classify whether a Cocholotoma septemspirale is male or female, regardless of the locality it comes from (there is no interaction of the two effects); females have significantly taller shells. Limitations of the study include its correlational nature. One issue with the study, for example, is that age might be a confounding variable, if these snails are the type that grows throughout their lifecycle.
Practice problems
- Finish the post-hoc t-tests for the effect of locality on shell width.
- Complete an analysis similar to the one above, using one of the variables other than shell.h as -your dependent variable. See if that variable would be of use in classifying the snails.
- Complete a new analysis of this pain/neuroimaging data set. Use sex and disease group as independent variables. Choose for your dependent variable one of the brain volumes.
See also
References
- Che, Annie, Cui, Jenny, and Dinov, Ivo (2009). SOCR Analyses: Implementation and Demonstration of a New Graphical Statistics Educational Toolkit. JSS, Vol. 30, Issue 3, Apr 2009.
- Che, A, Cui, J, and Dinov, ID (2009) SOCR Analyses – an Instructional Java Web-based Statistical Analysis Toolkit, JOLT, 5(1), 1-19, March 2009.
- Dinov, ID. Statistics Online Computational Resource, Journal of Statistical Software, Vol. 16, No. 1, 1-16, October 2006.
- Reichenbach F, Baur H, Neubert E (2012) Sexual dimorphism in shells of Cochlostoma septemspirale (Caenogastropoda, Cyclophoroidea, Diplommatinidae, Cochlostomatinae). ZooKeys 208: 1-16. doi:10.3897/zookeys.208.2869
- Baur H, Reichenbach F, Neubert E (2012) Data from: Sexual dimorphism in shells of Cochlostoma septemspirale (Caenogastropoda, Cyclophoroidea, Diplommatinidae, Cochlostomatinae). Dryad Digital Repository. doi:10.5061/dryad.ns7v7
Translate this page:
