SOCR EduMaterials Activities 2D PointSegmentation EM Mixture
From Socr
Contents |
SOCR Educational Materials - Activities - SOCR Activity Demonstrating Expectation Maximization and Mixture Modeling
Summary
This is activity demonstrates mixture modeling and expectation maximization (EM) applied to the problem of 2D point cluster segmentation.
Background
You may find useful this review the mathematics of Expectation Maximization and Mixture Modeling. In this activity we will demonstrate how the EM and mixture modeling may be used to obtain cluster classification of points in 2D. There are a number of problems where such segmentation is very important for solving a practical problem. 1D and 3D applications of the EM mixture modeling are also included at the end.
Exercises
Exercise 1: SOCR Charts Activity
- This exercise demonstrates the applications of expectation maximization and mixure modeling for cluster classification of points in 2D. Go to SOCR Charts and select Line Charts --> SOCR EM MixtureModelChart. The image below demonstrates the overall look-and-feel of the SOCR EM Mixture Model applet. Try adding several clusters of points and select different number of the kernels/mixtures you want to fit to this data. Notice the adaptive behavior of the algorithm.
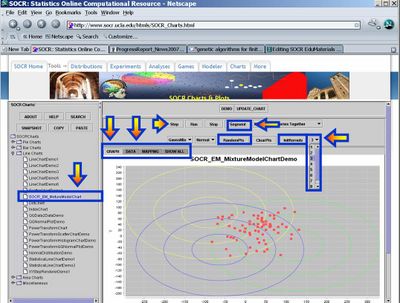
- Data: You can enter data (paired X,Y observations) either via the Data-Tab, using copy-and-paste, or via the add random points button (RandomPts). This applet was designed specifically so that the user may enter his/her own paired observations in tabular form. If you are not interested in data analysis, but want to explore more the properties of the EM mixture model you may try the second SOCR applet (SOCR Experiments, select Mixture Model EM Experiment from the drop down list of SOCR Experiments on the top-left), which allows you to manually add points by clicking on the graphing canvas.
- Applet specifications: You can fit one of two models to your data (Linear or elliptical Gaussian), see the GaussianMix button. The Normal button allows you to choose Slow, Normal and Fast speed for the iterative EM estimation. The ClearPts will remove all data and reset the applet. The InitKernels button re-initializes the kernels (location and size) and is useful for shaking the EM algorithm to escape local minima. The drop-down list on the top-right allows you to select the number of kernels you want to fit to this data. There is no exact method for determining this number in all situations (manually or automatically). Typically, one uses the physical or biological properties of the studied data/process to determine the appropriate integer value. The Step, Run and Stop buttons on the top have the natural functions associated with driving the iterative EM algorithm. The Segment button allows labeling/classification of the points once the EM algorithm has converged or is stopped.
Exercise 2: 1D and 3D Examples of SOCR EM Mixture Modeling
You may also see the action of the same SOCR EM Mixture modeling algorithm for analyzing 1D or 3D data.
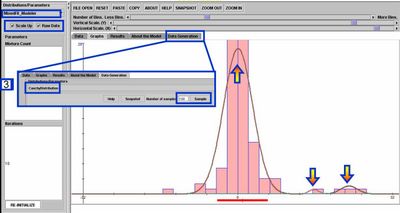
- For 1D data, you can see the EM mixture model fitting used by the SOCR Modeler to fit a polynomial, spectral or distribution model to (randomly sampled or observed) data. To see this, go to SOCR Modeler and select MixedFit_Modeler from the drop-down list of models on the top-left. The figure below shows the result of fitting a 3-kernel Mixture of Normal (Gaussian) distributions to the histogram of a random sample of 100 Cauchy random variables.
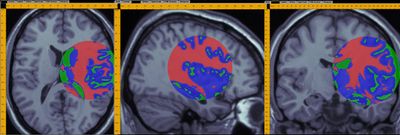
- A demonstration of a 3D data analysis using the SOCR EM Mixture model is included in the LONI Viz Manual. This shows how 3D brain imaging data may be segmented into three tissue types (White Matter, Gray Matter and Cerebrospinal Fluid). This is achieved by LONI Viz sending the segmentation tasks to SOCR and SOCR returning back the 3D segmented volumes which are superimposed dynamically on top of the initial anatomical brain imaging data in real time. The figure below illustrates this functionality. Other external computational tools could also invoke SOCR statistical computing resources directly by using the SOCR JAR binaries and the SOCR Documentation.
Questions
- How stable is the EM algorithm in finding a solution? Does this solution appear to be unique?
- What affects the convergence properties of the EM algorithm (data characteristics, number and properties of the starting initial kernel(s), etc.)?
References
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:
