SOCR EduMaterials Activities ApplicationsActivities BlackScholesOptionPricing
From Socr
(New page: == Black-Scholes option pricing model - Convergence of binomial == * Black-Scholes option pricing formula: <br> The value <math>C<math> of a European call option at time <math>t=0</math> ...)
Newer edit →
Revision as of 15:49, 3 August 2008
Black-Scholes option pricing model - Convergence of binomial
- Black-Scholes option pricing formula:
The value C < math > ofaEuropeancalloptionattime < math > t = 0 is:
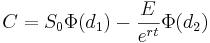
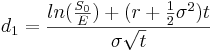
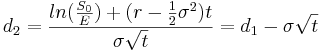
Where,
S0 Price of the stock at time t = 0
E Exercise price at expiration
r Continuously compounded risk-free interest
σ Annual standard deviation of the returns of the stock
t < math > Timetoexpirationinyears < br > < math > Φ(di) Cumulative probability at di of the standard normal distribution N(0,1)
- Binomial convergence to Black-Scholes option pricing formula:
The binomial formula converges to the Black-Scholes formula when
the number of periods n < math > islarge.Intheexamplebelowwevaluethecalloptionusingthebinomialformulafordifferentvaluesof < math > n and also using the Black-Scholes formula. We then plot the value of the call (from binomial) against the number of periods n < math > .ThevalueofthecallusingBlack − Scholesremainsthesameregardlessof < math > n. The data used for this example are:
Failed to parse (lexing error): S_0=\$30, \ E=\$29,\ R_f=0.05, \sigma=0.30,\ \mbox{Days to expiration}=40
.
- For the binomial option pricing calculations we divided the 40 days into intervals from 1 to 100 (by 1).
- The snapshot below from the SOCR Black Scholes Option Pricing model applet shows the path of the stock.
