SOCR EduMaterials Activities ApplicationsActivities BlackScholesOptionPricing
From Socr
| Line 29: | Line 29: | ||
the number of periods <math>n</math> is large. In the example below we value the call option using the binomial formula for different values of <math>n</math> and also using the Black-Scholes formula. We then plot the value of the call (from binomial) against the number of periods <math>n</math>. The value of the | the number of periods <math>n</math> is large. In the example below we value the call option using the binomial formula for different values of <math>n</math> and also using the Black-Scholes formula. We then plot the value of the call (from binomial) against the number of periods <math>n</math>. The value of the | ||
call using Black-Scholes remains the same regardless of <math>n</math>. The data used for this example are: | call using Black-Scholes remains the same regardless of <math>n</math>. The data used for this example are: | ||
| - | <math>S_0=\$30, \ E=\$29,\ R_f=0.05, \sigma=0.30,\ | + | <math>S_0=\$30</math>, \ E=\$29,\ R_f=0.05, \sigma=0.30,\ |
\mbox{Days to expiration}=40</math>. <br> | \mbox{Days to expiration}=40</math>. <br> | ||
* For the binomial option pricing calculations we divided the 40 days into intervals from 1 to 100 (by 1). | * For the binomial option pricing calculations we divided the 40 days into intervals from 1 to 100 (by 1). | ||
* The snapshot below from the SOCR Black Scholes Option Pricing model applet shows the path of the stock. | * The snapshot below from the SOCR Black Scholes Option Pricing model applet shows the path of the stock. | ||
Revision as of 15:51, 3 August 2008
Black-Scholes option pricing model - Convergence of binomial
- Black-Scholes option pricing formula:
The value C < math > ofaEuropeancalloptionattime < math > t = 0 is:
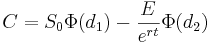
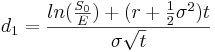
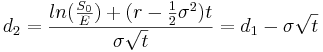
Where,
S0 Price of the stock at time t = 0
E Exercise price at expiration
r Continuously compounded risk-free interest
σ Annual standard deviation of the returns of the stock
t Time to expiration in years
Φ(di) Cumulative probability at di of the standard normal distribution N(0,1)
- Binomial convergence to Black-Scholes option pricing formula:
The binomial formula converges to the Black-Scholes formula when
the number of periods n is large. In the example below we value the call option using the binomial formula for different values of n and also using the Black-Scholes formula. We then plot the value of the call (from binomial) against the number of periods n. The value of the
call using Black-Scholes remains the same regardless of n. The data used for this example are:
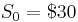 , \ E=\$29,\ R_f=0.05, \sigma=0.30,\
\mbox{Days to expiration}=40</math>.
, \ E=\$29,\ R_f=0.05, \sigma=0.30,\
\mbox{Days to expiration}=40</math>.
- For the binomial option pricing calculations we divided the 40 days into intervals from 1 to 100 (by 1).
- The snapshot below from the SOCR Black Scholes Option Pricing model applet shows the path of the stock.
