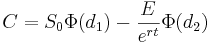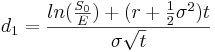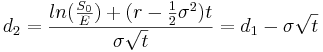SOCR EduMaterials Activities ApplicationsActivities BlackScholesOptionPricing
From Socr
(→Binomial convergence to Black-Scholes option pricing formula) |
(→Binomial convergence to Black-Scholes option pricing formula) |
||
| Line 26: | Line 26: | ||
* For the binomial option pricing calculations we divided the 40 days into intervals from 1 to 100 (by 1). | * For the binomial option pricing calculations we divided the 40 days into intervals from 1 to 100 (by 1). | ||
| - | * The snapshot below from the [http://www.socr.ucla.edu/htmls/app/ SOCR Black Scholes Option Pricing model applet] shows the convergence of the call price calculated by the binomial option pricing model to the price of the call calculated using the Black- | + | * The snapshot below from the [http://www.socr.ucla.edu/htmls/app/ SOCR Black Scholes Option Pricing model applet] shows the convergence of the call price calculated by the binomial option pricing model to the price of the call calculated using the Black-Scholes model. |
<br> | <br> | ||
Current revision as of 19:49, 3 August 2008
Contents |
SOCR Applications Activities - Black-Scholes Option Pricing Model (with Convergence of Binomial)
Description
You can access the Black-Scholes Option Pricing Model applet at the SOCR Applications Site, select Financial Applications --> BlackScholesOptionPricing.
Black-Scholes option pricing formula
The value C of a European call option at time t = 0 is:
Where,
- S0 Price of the stock at time t = 0
- E Exercise price at expiration
- r Continuously compounded risk-free interest
- σ Annual standard deviation of the returns of the stock
- t Time to expiration in years
- Φ(di) Cumulative probability at di of the standard normal distribution N(0,1)
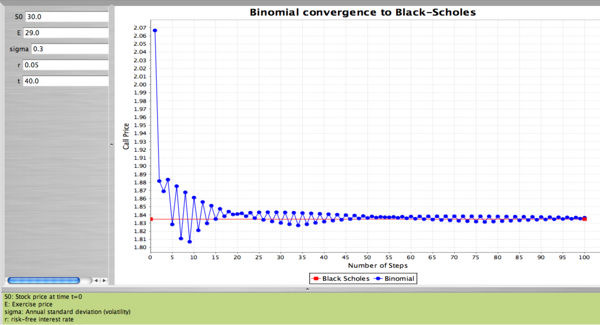
Binomial convergence to Black-Scholes option pricing formula
The binomial formula converges to the Black-Scholes formula when the number of periods n is large. In the example below we value the call option using the binomial formula for different values of n and also using the Black-Scholes formula. We then plot the value of the call (from binomial) against the number of periods n. The value of the call using Black-Scholes remains the same regardless of n. The data used for this example are:
-
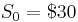 ,
, 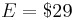 , Rf = 0.05, σ = 0.30,
, Rf = 0.05, σ = 0.30,
Days to expiration = 40.
- For the binomial option pricing calculations we divided the 40 days into intervals from 1 to 100 (by 1).
- The snapshot below from the SOCR Black Scholes Option Pricing model applet shows the convergence of the call price calculated by the binomial option pricing model to the price of the call calculated using the Black-Scholes model.
References
The materials above was partially taken from:
- Modern Portfolio Theory by Edwin J. Elton, Martin J. Gruber, Stephen J. Brown, and William N. Goetzmann, Sixth Edition, Wiley, 2003.
- Options, Futues, and Other Derivatives by John C. Hull, Sixth Edition, Pearson Prentice Hall, 2006.
- SOCR Applications Site
Translate this page: