SOCR EduMaterials Activities ApplicationsActivities Portfolio
From Socr
(→Portfolio theory) |
(→Portfolio Theory) |
||
| Line 1: | Line 1: | ||
| + | == Portfolio Theory == | ||
== Portfolio Theory == | == Portfolio Theory == | ||
| - | An investor has a certain amount of dollars to invest into two stocks <math>IBM</math> and <math>TEXACO</math>. A portion of the available funds will be invested into | + | An investor has a certain amount of dollars to invest into two stocks |
| - | IBM (denote this portion of the funds with <math>x_A</math> and the remaining funds | + | (<math>IBM</math> and <math>TEXACO</math>). A portion of the available funds will be invested into |
| + | IBM (denote this portion of the funds with <math>x_A</math>) and the remaining funds | ||
into TEXACO (denote it with <math>x_B</math>) - so <math>x_A+x_B=1</math>. The resulting portfolio | into TEXACO (denote it with <math>x_B</math>) - so <math>x_A+x_B=1</math>. The resulting portfolio | ||
will be <math>x_A R_A+x_B R_B</math>, where <math>R_A</math> is the monthly return of <math>IBM</math> and <math>R_B</math> is the | will be <math>x_A R_A+x_B R_B</math>, where <math>R_A</math> is the monthly return of <math>IBM</math> and <math>R_B</math> is the | ||
| - | monthly return of TEXACO. The goal here is to | + | monthly return of <math>TEXACO</math>. The goal here is to |
find the most efficient portfolios given a certain amount of risk. | find the most efficient portfolios given a certain amount of risk. | ||
Using market data from January 1980 until February 2001 we compute | Using market data from January 1980 until February 2001 we compute | ||
that <math>E(R_A)=0.010</math>, <math>E(R_B)=0.013</math>, <math>Var(R_A)=0.0061</math>, <math>Var(R_B)=0.0046</math>, and | that <math>E(R_A)=0.010</math>, <math>E(R_B)=0.013</math>, <math>Var(R_A)=0.0061</math>, <math>Var(R_B)=0.0046</math>, and | ||
| - | <math>Cov(R_A,R_B)=0.00062</math>. | + | <math>Cov(R_A,R_B)=0.00062</math>. \\ |
| - | + | We first want to minimize the variance of the portfolio. | |
| - | + | This will be: | |
<math> | <math> | ||
| - | \mbox{Minimize} \ \ mbox{Var}(x_A R_A+x_BR_B) | + | \mbox{Minimize} \ \ \mbox{Var}(x_A R_A+x_BR_B) \\ |
| + | \mbox{subject to} \ \ x_A+x_B=1 | ||
</math> | </math> | ||
| + | Or | ||
<math> | <math> | ||
| + | \mbox{Minimize} \ \ x_A^2 Var(R_A)+x_B^2 Var(R_B) + 2x_Ax_BCov(R_A,R_B) \\ | ||
\mbox{subject to} \ \ x_A+x_B=1 | \mbox{subject to} \ \ x_A+x_B=1 | ||
</math> | </math> | ||
| + | Therefore our goal is to find <math>x_A</math> and <math>x_B</math>, the percentage of the | ||
| + | available funds that will be invested in each stock. Substituting | ||
| + | <math>x_B=1-x_A</math> into the equation of the variance we get | ||
| + | <math> | ||
| + | x_A^2 Var(R_A)+(1-x_A)^2 Var(R_B) + 2x_A(1-x_A)Cov(R_A,R_B) | ||
| + | </math> | ||
| + | To minimize the above exression we take the derivative with respect to | ||
| + | <math>x_A</math>, set it equal to zero and solve for <math>x_A</math>. The result is: | ||
| + | <math> | ||
| + | x_A=\frac{Var(R_B) - Cov(R_A,R_B)}{Var(R_A)+Var(R_B)-2Cov(R_A,R_B)} | ||
| + | </math> | ||
| + | and therefore | ||
| + | <math> | ||
| + | x_B=\frac{Var(R_A) - Cov(R_A,R_B)}{Var(R_A)+Var(R_B)-2Cov(R_A,R_B)} | ||
| + | </math> | ||
| + | The values of <math>x_a</math> and <math>x_B</math> are: | ||
| + | <math> | ||
| + | x_a=\frac{0.0046-0.0062}{0.0061+0.0046-2(0.00062)} \Rightarrow x_A=0.42. | ||
| + | </math> | ||
| + | and <math>x_B=1-x_A=1-0.42 \Rightarrow x_B=0.58</math>. Therefore if the investor invests | ||
| + | <math>42 \%</math> of the available funds into <math>IBM</math> and the remaining <math>58 \%</math> | ||
| + | into <math>TEXACO</math> the variance of the portfolio will be minimum and equal to: | ||
| + | <math> | ||
| + | Var(0.42R_A+0.58R_B)=0.42^2(0.0061)+0.58^2(0.0046)+2(0.42)(0.58)(0.00062) | ||
| + | =0.002926. | ||
| + | </math> | ||
| + | The corresponding expected return of this porfolio will be: | ||
| + | <math> | ||
| + | E(0.42R_A+0.58R_B)=0.42(0.010)+0.58(0.013)=0.01174. | ||
| + | </math> | ||
| + | We can try many other combinations of <math>x_A</math> and <math>x_B</math> (but always <math>x_A+x_B=1</math>) | ||
| + | and compute the risk and return for each resulting portfolio. This is | ||
| + | shown in the table and the graph below. \<math>0.05in] | ||
Revision as of 05:47, 3 August 2008
Portfolio Theory
Portfolio Theory
An investor has a certain amount of dollars to invest into two stocks (IBM and TEXACO). A portion of the available funds will be invested into IBM (denote this portion of the funds with xA) and the remaining funds into TEXACO (denote it with xB) - so xA + xB = 1. The resulting portfolio will be xARA + xBRB, where RA is the monthly return of IBM and RB is the monthly return of TEXACO. The goal here is to find the most efficient portfolios given a certain amount of risk. Using market data from January 1980 until February 2001 we compute that E(RA) = 0.010, E(RB) = 0.013, Var(RA) = 0.0061, Var(RB) = 0.0046, and Cov(RA,RB) = 0.00062. \\ We first want to minimize the variance of the portfolio. This will be: Failed to parse (syntax error): \mbox{Minimize} \ \ \mbox{Var}(x_A R_A+x_BR_B) \\ \mbox{subject to} \ \ x_A+x_B=1
Or Failed to parse (syntax error): \mbox{Minimize} \ \ x_A^2 Var(R_A)+x_B^2 Var(R_B) + 2x_Ax_BCov(R_A,R_B) \\ \mbox{subject to} \ \ x_A+x_B=1
Therefore our goal is to find xA and xB, the percentage of the
available funds that will be invested in each stock. Substituting
xB = 1 − xA into the equation of the variance we get
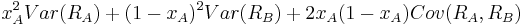 To minimize the above exression we take the derivative with respect to
xA, set it equal to zero and solve for xA. The result is:
To minimize the above exression we take the derivative with respect to
xA, set it equal to zero and solve for xA. The result is:
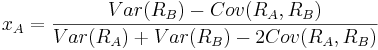 and therefore
and therefore
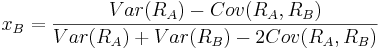 The values of xa and xB are:
The values of xa and xB are:
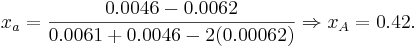 and
and 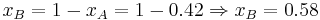 . Therefore if the investor invests
. Therefore if the investor invests
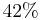 of the available funds into IBM and the remaining
of the available funds into IBM and the remaining 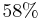 into TEXACO the variance of the portfolio will be minimum and equal to:
Var(0.42RA + 0.58RB) = 0.422(0.0061) + 0.582(0.0046) + 2(0.42)(0.58)(0.00062) = 0.002926.
The corresponding expected return of this porfolio will be:
E(0.42RA + 0.58RB) = 0.42(0.010) + 0.58(0.013) = 0.01174.
We can try many other combinations of xA and xB (but always xA + xB = 1)
and compute the risk and return for each resulting portfolio. This is
shown in the table and the graph below. \0.05in]
into TEXACO the variance of the portfolio will be minimum and equal to:
Var(0.42RA + 0.58RB) = 0.422(0.0061) + 0.582(0.0046) + 2(0.42)(0.58)(0.00062) = 0.002926.
The corresponding expected return of this porfolio will be:
E(0.42RA + 0.58RB) = 0.42(0.010) + 0.58(0.013) = 0.01174.
We can try many other combinations of xA and xB (but always xA + xB = 1)
and compute the risk and return for each resulting portfolio. This is
shown in the table and the graph below. \0.05in]
