SOCR EduMaterials Activities ApplicationsActivities Portfolio
From Socr
(→Portfolio Theory) |
(→Portfolio Theory) |
||
| Line 1: | Line 1: | ||
== Portfolio Theory == | == Portfolio Theory == | ||
| + | |||
| + | * '''Description''': You can access the portfolio applet at http://www.socr.ucla.edu/htmls/app/ . | ||
An investor has a certain amount of dollars to invest into two stocks | An investor has a certain amount of dollars to invest into two stocks | ||
Revision as of 15:22, 3 August 2008
Portfolio Theory
- Description: You can access the portfolio applet at http://www.socr.ucla.edu/htmls/app/ .
An investor has a certain amount of dollars to invest into two stocks
(IBM and TEXACO). A portion of the available funds will be invested into
IBM (denote this portion of the funds with xA) and the remaining funds
into TEXACO (denote it with xB) - so xA + xB = 1. The resulting portfolio
will be xARA + xBRB, where RA is the monthly return of IBM and RB is the
monthly return of TEXACO. The goal here is to
find the most efficient portfolios given a certain amount of risk.
Using market data from January 1980 until February 2001 we compute
that E(RA) = 0.010, E(RB) = 0.013, Var(RA) = 0.0061, Var(RB) = 0.0046, and
Cov(RA,RB) = 0.00062. We first want to minimize the variance of the portfolio.
This will be:
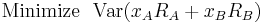
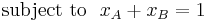 Or
Or
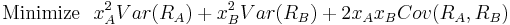
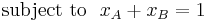
Therefore our goal is to find xA and xB, the percentage of the
available funds that will be invested in each stock. Substituting
xB = 1 − xA into the equation of the variance we get
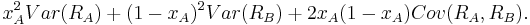
To minimize the above exression we take the derivative with respect to
xA, set it equal to zero and solve for xA. The result is:
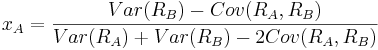
and therefore
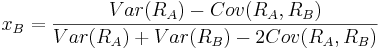
The values of xA and xB are:
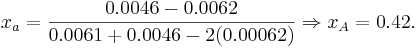 and
and 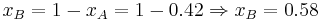 . Therefore if the investor invests
. Therefore if the investor invests
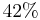 of the available funds into IBM and the remaining
of the available funds into IBM and the remaining 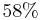 into TEXACO the variance of the portfolio will be minimum and equal to:
Var(0.42RA + 0.58RB) = 0.422(0.0061) + 0.582(0.0046) + 2(0.42)(0.58)(0.00062) = 0.002926.
The corresponding expected return of this porfolio will be:
E(0.42RA + 0.58RB) = 0.42(0.010) + 0.58(0.013) = 0.01174.
We can try many other combinations of xA and xB (but always xA + xB = 1)
and compute the risk and return for each resulting portfolio. This is
shown in the table and the graph below.
into TEXACO the variance of the portfolio will be minimum and equal to:
Var(0.42RA + 0.58RB) = 0.422(0.0061) + 0.582(0.0046) + 2(0.42)(0.58)(0.00062) = 0.002926.
The corresponding expected return of this porfolio will be:
E(0.42RA + 0.58RB) = 0.42(0.010) + 0.58(0.013) = 0.01174.
We can try many other combinations of xA and xB (but always xA + xB = 1)
and compute the risk and return for each resulting portfolio. This is
shown in the table and the graph below.
| xA | xB | Risk (σ2) | Return | Risk (σ) |
|---|---|---|---|---|
| 1.00 | 0.00 | 0.006100 | 0.01000 | 0.078102 |
| 0.95 | 0.05 | 0.005576 | 0.01015 | 0.074670 |
| 0.90 | 0.10 | 0.005099 | 0.01030 | 0.071404 |
| 0.85 | 0.15 | 0.004669 | 0.01045 | 0.068329 |
| 0.80 | 0.20 | 0.004286 | 0.01060 | 0.065471 |
| 0.75 | 0.25 | 0.003951 | 0.01075 | 0.062859 |
| 0.70 | 0.30 | 0.003663 | 0.01090 | 0.060526 |
| 0.65 | 0.35 | 0.003423 | 0.01105 | 0.058505 |
| 0.60 | 0.40 | 0.003230 | 0.01120 | 0.056830 |
| 0.55 | 0.45 | 0.003084 | 0.01135 | 0.055531 |
| 0.50 | 0.50 | 0.002985 | 0.01150 | 0.054635 |
| 0.42 | 0.58 | 0.002926 | 0.01174 | 0.054088 |
| 0.40 | 0.60 | 0.002930 | 0.01180 | 0.054126 |
| 0.35 | 0.65 | 0.002973 | 0.01195 | 0.054524 |
| 0.30 | 0.70 | 0.003063 | 0.01210 | 0.055348 |
| 0.25 | 0.75 | 0.003201 | 0.01225 | 0.056580 |
| 0.20 | 0.80 | 0.003386 | 0.01240 | 0.058193 |
| 0.15 | 0.85 | 0.003619 | 0.01255 | 0.060157 |
| 0.10 | 0.90 | 0.003899 | 0.01270 | 0.062439 |
| 0.05 | 0.95 | 0.004226 | 0.01285 | 0.065005 |
| 0.00 | 1.00 | 0.004600 | 0.01300 | 0.067823 |
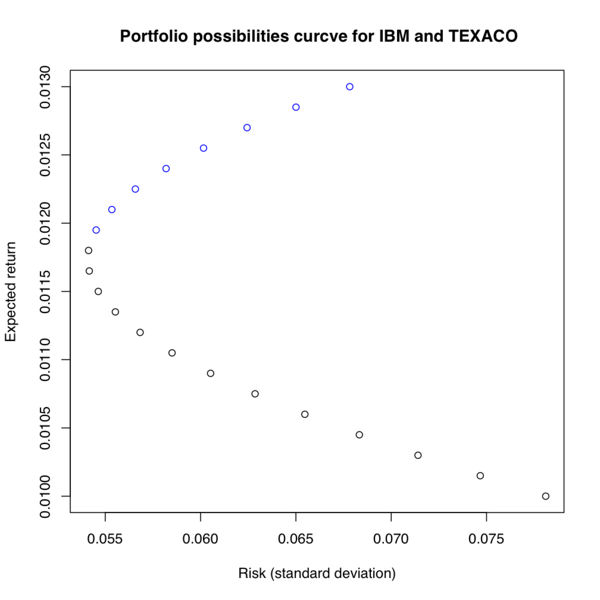
For the above calculations short selling was not allowed (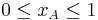 and
and
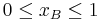 , in addition to xA + xB = 1). We note here that the efficient portfolios are located on the top part of the graph between the minimum risk portfolio point and the maximum return portfolio point, which is called the efficient frontier (the blue portion of the graph). Efficient portfolios should provide higher expected return for the same level of risk or lower risk for the same level of expected return.
, in addition to xA + xB = 1). We note here that the efficient portfolios are located on the top part of the graph between the minimum risk portfolio point and the maximum return portfolio point, which is called the efficient frontier (the blue portion of the graph). Efficient portfolios should provide higher expected return for the same level of risk or lower risk for the same level of expected return.
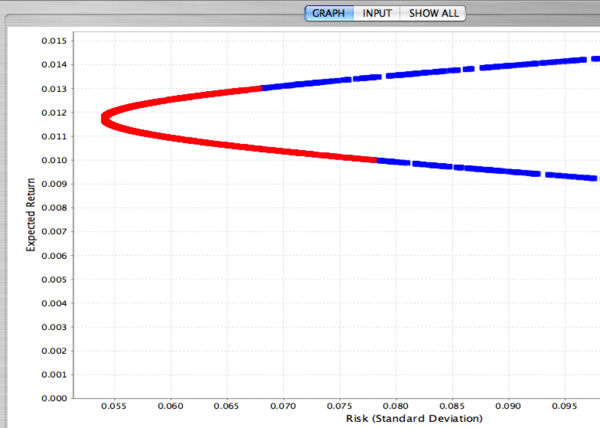
If short sales are allowed, which means that the investor can sell a stock that he or she does not own the graph has the same shape but now with more possibilities. The investor can have very large expected return but this will be associated with very large risk. The constraint here is only xA + xB = 1, since either xA < math > or < math > xB can be negative. The snapshot below from the SOCR applet shows the ``short sales scenario" for the IBM and TEXACO stocks. The blue portion of the portfolio possibilities curve occurs when short sales are allowed, while the red portion corresponds to the case when short sales are not allowed.
When the investor faces the efficient frontier when short sales are allowed and he or she can lend or borrow at the risk-free interest rate the efficient frontier will change in the following way: Let x be the portion of the investor's wealth invested in portfolio A that lies on the efficient frontier, and 1 − x the the portion invested in a risk-free asset. This combination is a new portfolio and has
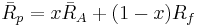
where Rf is the return of the risk-free asset. The variance of this combination is simply
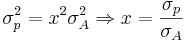
From the last two equations we get
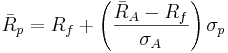
This is an equation of a straight line. On this line we find all the possible combinations of portfolio A and the risk-free rate. Another investor can choose to combine the risk-free rate with portfolio B or portfolio C. Clearly, for the same level risk the combinations that lie on the Rf − B line have higher expected return than those on the line Rf − A (see figure below). And Rf − C will produce combinations that have higher return than those on Rf − B for the same level of risk, etc.
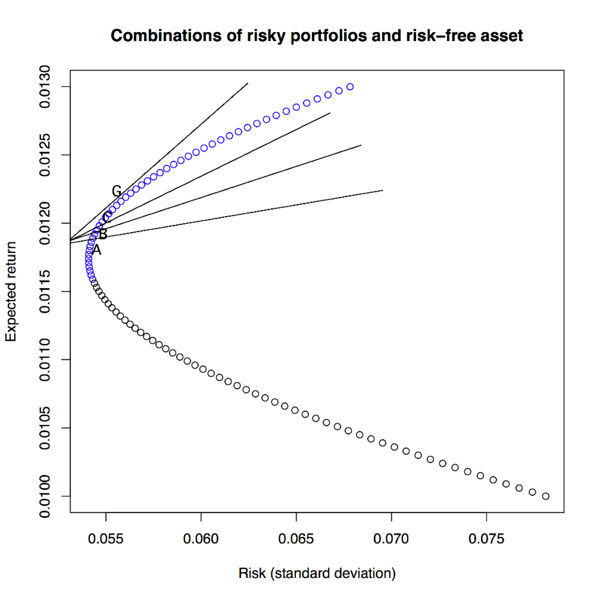
The solution, therefore, is to find the point of tangency of this line to the efficient frontier. Let's call this point G. To find this point we want to maximize the slope of the line in (1) as follows:
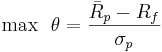 Subject to
Subject to
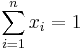 Since,
Since,
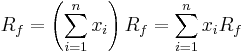 we can write the maximization problem as
we can write the maximization problem as
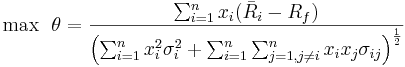
or
![\mbox{max} \ \ \theta=\left[\sum_{i=1}^n x_i (\bar R_i - R_f)\right]
\left[\sum_{i=1}^n x_i^2 \sigma_i^2 + \sum_{i=1}^n \sum_{j=1, j \ne i}^n x_i x_j \sigma_{ij}\right]^{-\frac{1}{2}}](/socr/uploads/math/0/b/9/0b9de3e6da1231d579ef5f43fc8f1853.png)
Take now the partial derivative with respect to each 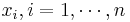 , set them equal to zero and solve. Let's find the partial derivative w.r.t. xk:
, set them equal to zero and solve. Let's find the partial derivative w.r.t. xk:
![\frac{\partial \theta}{\partial x_k} =
(\bar R_k - R_f)\left[\sum_{i=1}^n x_i^2 \sigma_i^2 + \sum_{i=1}^n \sum_{j=1, j \ne i}^n x_i x_j \sigma_{ij}\right]^{-\frac{1}{2}} +
\left[\sum_{i=1}^n x_i(\bar R_i - R_f)\right]
\left[2x_k\sigma_k^2 + 2 \sum_{j=1, j \ne k}^n x_j \sigma_{kj}\right] \times
\left[\sum_{i=1}^n x_i^2 \sigma_i^2 + \sum_{i=1}^n \sum_{j=1, j \ne i}^n x_i x_j \sigma_{ij}\right]^{-\frac{3}{2}} \times (-\frac{1}{2}) = 0](/socr/uploads/math/3/b/2/3b21c3cbb8fe3b48c09781505085fe88.png)
Multiply both sides by
![\left[\sum_{i=1}^n x_i^2 \sigma_i^2 + \sum_{i=1}^n \sum_{j=1, j \ne i}^n x_i x_j \sigma_{ij}\right]^{\frac{1}{2}} \ \ \ \mbox{to get}](/socr/uploads/math/d/7/2/d728e973c6bb13199932fffe13b06f76.png)
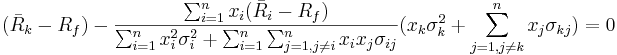
Now, if we let
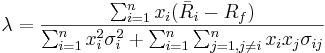
the previous expression will be
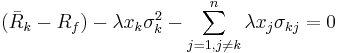
or
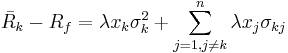
Let's define now a new variable,
zk = λxk
and finally
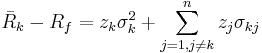 We have one equation like (2) for each
We have one equation like (2) for each  . Here they are:
. Here they are:
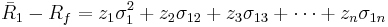
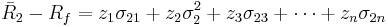



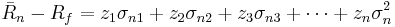
The solution involves solving the system of these simultaneous equations, which can be written in matrix form as:
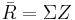 where Σ is the variance-covariance matrix of the returns of the n stocks. To solve for Z:
where Σ is the variance-covariance matrix of the returns of the n stocks. To solve for Z:
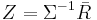
Once we find the zi's it is easy to find the xi's (the fraction of funds to be invested in each security). Earlier we defined
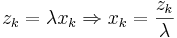 We need to find λ as follows:
We need to find λ as follows:
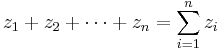
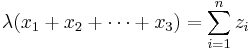
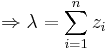
Therefore,
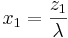
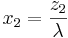
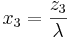



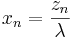
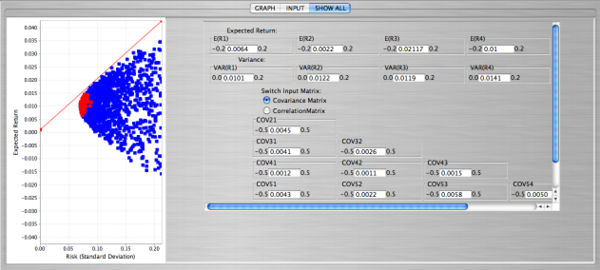
The snapshot form the SOCR portfolio applet shows an example with 5 stocks. Again, the red points in the applet correspond to the case when short sales are not allowed. The point of tangency can be found with a choice of the risk-free rate that can be entered in the input dialog box.
The materials above was partially taken from Modern Portfolio Theory by Edwin J. Elton, Martin J. Gruber, Stephen J. Brown, and William N. Goetzmann, Sixth Edition, Wiley, 2003.
