SOCR EduMaterials Activities BMI Modeling Activity
From Socr
Contents |
SOCR Educational Materials - Activities - SOCR Body Mass Index (BMI) Activity and Applications of the Chi-Squared Test
Often times when solving a problem from intro-level textbooks, we are told to assume that a population follows a normal distribution. Other times, a graph of the data will allow us to assume some degree of normality. This allows the use of a number of statistical analyses later on.
Motivation and Goals
The following activity will demonstrate one of the ways to test for normality, using the Chi-Squared test for Goodness-of-Fit. The model to fit will be the normal model. We will run this test on a human characteristic often assumed to fit at least some kind of normal model: BMI.
Summary
This activity uses a simplified version of the BMI data sets found here. Four cases of data were excluded due to extremely high BMIs that hinted at a mistake in the entry process. 10 variables from the original dataset were left out in the dataset presented here, though the same process presented here may be used on them for additional practice.
Data
Data Description
- Number of cases: 248
- Variables
- Underwater Density – Density determined via a graduated-cylinder type test
- Body fat—Calculated body density and tissue-type proportions using Siri’s equation (see the full dataset page)
- Height
- Weight
- BMI—Body Mass Index, calculated as \( \frac{weight}{height^2} \).
Data Summary
| Statistic | Underwater_Density_(\( \frac{g}{cm^3}\)) | Body_Fat | Height(m) | Weight_(kg) | BMI |
|---|---|---|---|---|---|
| Mean | 1.0562 | 18.854 | 1.787 | 80.547 | 25.18643319 |
| SD | 0.0184 | 8.0663 | 0.0659 | 12.0076 | 3.146481308 |
Raw Dataset
| Underwater_Density(g/cm3) | Body_Fat | Height(m) | Weight(kg) | BMI |
|---|---|---|---|---|
| 1.0708 | 12.3 | 1.72085 | 69.96662 | 23.6268 |
| 1.0853 | 6.1 | 1.83515 | 78.58488 | 23.33436 |
| 1.0414 | 25.3 | 1.68275 | 69.85322 | 24.66876 |
| 1.0751 | 10.4 | 1.83515 | 83.80119 | 24.88325 |
| 1.034 | 28.7 | 1.80975 | 83.57439 | 25.51738 |
| 1.0502 | 20.9 | 1.89865 | 95.3678 | 26.45525 |
| 1.0549 | 19.2 | 1.77165 | 82.10022 | 26.15703 |
| 1.0704 | 12.4 | 1.8415 | 79.83226 | 23.54155 |
| 1.09 | 4.1 | 1.8796 | 86.63614 | 24.5227 |
| 1.0722 | 11.7 | 1.8669 | 89.92469 | 25.80102 |
| 1.083 | 7.1 | 1.8923 | 84.48158 | 23.59294 |
| 1.0812 | 7.8 | 1.9304 | 97.97595 | 26.29208 |
| 1.0513 | 20.8 | 1.7653 | 81.87342 | 26.27277 |
| 1.0505 | 21.2 | 1.80975 | 93.09983 | 28.42574 |
| 1.0484 | 22.1 | 1.7653 | 85.16197 | 27.32805 |
| 1.0512 | 20.9 | 1.6764 | 73.82216 | 26.26827 |
| 1.0333 | 29 | 1.8034 | 88.79071 | 27.3013 |
| 1.0468 | 22.9 | 1.8034 | 94.9142 | 29.18415 |
| 1.0622 | 16 | 1.72085 | 83.3476 | 28.14538 |
| 1.061 | 16.5 | 1.8669 | 96.04818 | 27.55796 |
| 1.0551 | 19.1 | 1.7272 | 81.19303 | 27.21658 |
| 1.064 | 15.2 | 1.77165 | 90.94527 | 28.97505 |
| 1.0631 | 15.6 | 1.73355 | 63.61633 | 21.16878 |
| 1.0584 | 17.7 | 1.778 | 67.47187 | 21.34319 |
| 1.0668 | 14 | 1.72085 | 68.60585 | 23.16728 |
| 1.0911 | 3.7 | 1.8161 | 72.23458 | 21.90109 |
| 1.0811 | 7.9 | 1.7145 | 59.6474 | 20.29161 |
| 1.0468 | 22.9 | 1.7145 | 67.13167 | 22.83771 |
| 1.091 | 3.7 | 1.64465 | 60.44118 | 22.34529 |
| 1.079 | 8.8 | 1.7526 | 72.91497 | 23.73838 |
| 1.0716 | 11.9 | 1.87325 | 82.55381 | 23.52587 |
| 1.0862 | 5.7 | 1.80975 | 72.68818 | 22.19354 |
| 1.0719 | 11.8 | 1.80975 | 76.20352 | 23.26686 |
| 1.0502 | 21.3 | 1.8034 | 99.10993 | 30.47425 |
| 1.0263 | 32.3 | 1.8669 | 112.1507 | 32.17806 |
| 1.0101 | 40.1 | 1.651 | 86.97634 | 31.90854 |
| 1.0438 | 24.2 | 1.778 | 91.73906 | 29.01956 |
| 1.0346 | 28.4 | 1.73355 | 89.2443 | 29.69667 |
| 1.0258 | 32.6 | 1.7018 | 92.07925 | 31.79397 |
| 1.0279 | 31.6 | 1.778 | 98.42954 | 31.13594 |
| 1.0269 | 32 | 1.8161 | 96.16158 | 29.15561 |
| 1.0814 | 7.7 | 1.7272 | 56.81244 | 19.044 |
| 1.067 | 13.9 | 1.86055 | 74.50255 | 21.52229 |
| 1.0742 | 10.8 | 1.7145 | 60.55458 | 20.60023 |
| 1.0665 | 5.6 | 1.80975 | 67.35847 | 20.56625 |
| 1.0678 | 13.6 | 1.7399 | 61.57516 | 20.34028 |
| 1.0903 | 4 | 1.69545 | 57.83303 | 20.11898 |
| 1.0756 | 10.2 | 1.83515 | 71.78099 | 21.31407 |
| 1.084 | 6.6 | 1.7526 | 63.16274 | 20.56342 |
| 1.0807 | 8 | 1.72085 | 62.25555 | 21.02287 |
| 1.0848 | 6.3 | 1.8669 | 69.28623 | 19.87947 |
| 1.0906 | 3.9 | 1.7145 | 61.80196 | 21.02458 |
| 1.0473 | 22.6 | 1.8288 | 89.81129 | 26.85335 |
| 1.0524 | 20.4 | 1.7272 | 82.32702 | 27.5967 |
| 1.0356 | 28 | 1.7653 | 91.28546 | 29.29305 |
| 1.028 | 31.5 | 1.79705 | 91.85245 | 28.44267 |
| 1.043 | 24.6 | 1.67005 | 81.53323 | 29.23316 |
| 1.0396 | 26.1 | 1.86055 | 97.97595 | 28.30328 |
| 1.0317 | 29.8 | 1.7399 | 81.07964 | 26.78325 |
| 1.0298 | 30.7 | 1.78435 | 87.65673 | 27.5312 |
| 1.0403 | 25.8 | 1.7018 | 80.73944 | 27.87845 |
| 1.0264 | 32.3 | 1.778 | 93.21323 | 29.48588 |
| 1.0313 | 30 | 1.7145 | 83.2342 | 28.31567 |
| 1.0499 | 21.5 | 1.79705 | 68.71924 | 21.27933 |
| 1.0673 | 13.8 | 1.8161 | 70.19342 | 21.28222 |
| 1.0847 | 6.3 | 1.75895 | 70.42022 | 22.76095 |
| 1.0693 | 12.9 | 1.8161 | 71.1006 | 21.55727 |
| 1.0439 | 24.3 | 1.8161 | 75.97672 | 23.03568 |
| 1.0788 | 8.8 | 1.74625 | 66.56468 | 21.82886 |
| 1.0796 | 8.5 | 1.87325 | 72.91497 | 20.77903 |
| 1.068 | 13.5 | 1.6256 | 56.69905 | 21.45598 |
| 1.072 | 11.8 | 1.67005 | 64.86371 | 23.25642 |
| 1.0666 | 18.5 | 1.7145 | 67.24507 | 22.87628 |
| 1.079 | 8.8 | 1.7653 | 73.70876 | 23.65277 |
| 1.0483 | 22.2 | 1.7399 | 80.62604 | 26.63341 |
| 1.0498 | 21.5 | 1.78435 | 73.14177 | 22.97235 |
| 1.056 | 18.8 | 1.75895 | 77.67769 | 25.10668 |
| 1.0283 | 31.4 | 1.72085 | 74.27575 | 25.08193 |
| 1.0382 | 26.8 | 1.70815 | 68.15225 | 23.3576 |
| 1.0568 | 18.4 | 1.84785 | 86.29595 | 25.27301 |
| 1.0377 | 27 | 1.778 | 77.4509 | 24.49982 |
| 1.0378 | 27 | 1.75895 | 76.20352 | 24.63021 |
| 1.0386 | 26.6 | 1.7145 | 75.74993 | 25.76958 |
| 1.0648 | 14.9 | 1.70815 | 71.5542 | 24.52354 |
| 1.0462 | 23.1 | 1.67005 | 72.57478 | 26.02117 |
| 1.08 | 8.3 | 1.8415 | 80.17245 | 23.64186 |
| 1.0666 | 14.1 | 1.8542 | 79.83226 | 23.22016 |
| 1.052 | 20.5 | 1.778 | 80.28585 | 25.3966 |
| 1.0573 | 18.2 | 1.7653 | 81.53323 | 26.16361 |
| 1.0795 | 8.5 | 1.7907 | 74.95614 | 23.37553 |
| 1.0424 | 24.9 | 1.82245 | 87.31653 | 26.28968 |
| 1.0785 | 9 | 1.8923 | 83.57439 | 23.33959 |
| 1.0991 | 17.4 | 1.97485 | 101.8315 | 26.11042 |
| 1.077 | 9.6 | 1.86055 | 85.61556 | 24.73261 |
| 1.073 | 11.3 | 1.6891 | 73.70876 | 25.83499 |
| 1.0582 | 17.8 | 1.73355 | 70.98721 | 23.62149 |
| 1.0484 | 22.2 | 1.8288 | 89.3577 | 26.71773 |
| 1.0506 | 21.2 | 1.8669 | 90.03809 | 25.83355 |
| 1.0524 | 20.4 | 1.8288 | 78.81167 | 23.56449 |
| 1.053 | 20.1 | 1.80975 | 78.35808 | 23.92471 |
| 1.048 | 22.3 | 1.87325 | 89.2443 | 25.4325 |
| 1.0412 | 25.4 | 1.75895 | 80.28585 | 25.94968 |
| 1.0578 | 18 | 1.7399 | 75.06954 | 24.79792 |
| 1.0547 | 19.3 | 1.8669 | 90.83187 | 26.0613 |
| 1.0569 | 18.3 | 1.88595 | 92.19265 | 25.92006 |
| 1.0593 | 17.3 | 1.9177 | 87.99692 | 23.92799 |
| 1.05 | 21.4 | 1.75895 | 76.43031 | 24.70351 |
| 1.0538 | 19.7 | 1.7399 | 77.4509 | 25.58456 |
| 1.0355 | 28 | 1.778 | 83.1208 | 26.29337 |
| 1.0486 | 22.1 | 1.778 | 80.85284 | 25.57595 |
| 1.0503 | 21.3 | 1.78435 | 73.93556 | 23.22166 |
| 1.0384 | 26.7 | 1.82245 | 79.49206 | 23.93385 |
| 1.0607 | 16.7 | 1.75895 | 71.66759 | 23.16412 |
| 1.0529 | 20.1 | 1.84785 | 80.39925 | 23.54608 |
| 1.0671 | 13.9 | 1.8288 | 81.19303 | 24.27651 |
| 1.0404 | 25.8 | 1.8796 | 86.63614 | 24.5227 |
| 1.0575 | 18.1 | 1.83515 | 85.04857 | 25.25363 |
| 1.0358 | 27.9 | 1.8923 | 93.66682 | 26.15808 |
| 1.0414 | 25.3 | 1.8161 | 84.02799 | 25.47678 |
| 1.0652 | 14.7 | 1.74625 | 72.68818 | 23.83696 |
| 1.0623 | 16 | 1.69545 | 68.71924 | 23.90608 |
| 1.0674 | 13.8 | 1.6891 | 73.02837 | 25.59652 |
| 1.0587 | 17.5 | 1.7018 | 75.74993 | 26.15563 |
| 1.0373 | 27.2 | 1.74625 | 80.51265 | 26.40288 |
| 1.059 | 17.4 | 1.72085 | 69.05944 | 23.32046 |
| 1.0515 | 20.8 | 1.86055 | 87.20313 | 25.19123 |
| 1.0648 | 14.9 | 1.77165 | 74.95614 | 23.88094 |
| 1.0575 | 18.1 | 1.8161 | 77.90449 | 23.62017 |
| 1.0472 | 22.7 | 1.7907 | 77.67769 | 24.22427 |
| 1.0452 | 23.6 | 1.86055 | 89.3577 | 25.81364 |
| 1.0398 | 26.1 | 1.69545 | 71.214 | 24.77396 |
| 1.0435 | 24.4 | 1.7653 | 76.31692 | 24.48972 |
| 1.0374 | 27.1 | 1.77165 | 84.36818 | 26.8796 |
| 1.0491 | 21.8 | 1.79705 | 75.63653 | 23.42131 |
| 1.0325 | 29.4 | 1.8796 | 85.16197 | 24.10543 |
| 1.0481 | 22.4 | 1.80975 | 76.31692 | 23.30149 |
| 1.0522 | 20.4 | 1.905 | 96.50178 | 26.59165 |
| 1.0422 | 24.9 | 1.8034 | 80.17245 | 24.65137 |
| 1.0571 | 18.3 | 1.7653 | 78.58488 | 25.2175 |
| 1.0459 | 23.3 | 1.72085 | 75.74993 | 25.57974 |
| 1.0775 | 9.4 | 1.83515 | 72.46138 | 21.5161 |
| 1.0754 | 10.3 | 1.9685 | 85.3434 | 22.02415 |
| 1.0664 | 14.2 | 1.79705 | 70.76041 | 21.91139 |
| 1.055 | 19.2 | 1.84785 | 94.57401 | 27.69736 |
| 1.0322 | 29.6 | 1.77165 | 93.66682 | 29.84214 |
| 1.0873 | 5.3 | 1.8415 | 65.2039 | 19.22782 |
| 1.0416 | 25.2 | 1.78435 | 101.1511 | 31.76951 |
| 1.0776 | 9.4 | 1.7526 | 69.05944 | 22.48316 |
| 1.0542 | 19.6 | 1.8923 | 109.656 | 30.62333 |
| 1.0758 | 10.1 | 1.83515 | 66.22449 | 19.66416 |
| 1.061 | 16.5 | 1.70815 | 71.1006 | 24.36808 |
| 1.051 | 21 | 1.8669 | 90.83187 | 26.0613 |
| 1.0594 | 17.3 | 1.91135 | 77.79109 | 21.29362 |
| 1.0287 | 31.2 | 1.7526 | 93.32663 | 30.38365 |
| 1.0761 | 10 | 1.83515 | 82.78061 | 24.5802 |
| 1.0704 | 12.5 | 1.74625 | 61.91536 | 20.30419 |
| 1.0477 | 22.5 | 1.8161 | 80.39925 | 24.37656 |
| 1.0775 | 9.4 | 1.83515 | 68.60585 | 20.37127 |
| 1.0653 | 14.6 | 1.8542 | 88.9041 | 25.85882 |
| 1.069 | 13 | 1.74625 | 83.57439 | 27.40693 |
| 1.0644 | 15.1 | 1.7907 | 63.50293 | 19.80378 |
| 1.037 | 27.3 | 1.8288 | 99.22333 | 29.66753 |
| 1.0549 | 19.2 | 1.87325 | 98.42954 | 28.05007 |
| 1.0492 | 21.8 | 1.7272 | 75.40973 | 25.27797 |
| 1.0525 | 20.3 | 1.83515 | 101.9449 | 30.27069 |
| 1.018 | 34.3 | 1.7653 | 103.5325 | 33.22306 |
| 1.061 | 16.5 | 1.7653 | 78.35808 | 25.14472 |
| 1.0926 | 3 | 1.72085 | 69.05944 | 23.32046 |
| 1.0983 | 0.7 | 1.6637 | 57.03924 | 20.60742 |
| 1.0521 | 20.5 | 1.8034 | 80.39925 | 24.7211 |
| 1.0603 | 16.9 | 1.8161 | 79.94566 | 24.23904 |
| 1.0414 | 25.3 | 1.82245 | 102.8521 | 30.9672 |
| 1.0763 | 9.9 | 1.75895 | 65.88429 | 21.29486 |
| 1.0689 | 13.1 | 1.7018 | 68.49245 | 23.6497 |
| 1.0316 | 29.9 | 1.8161 | 109.4292 | 33.17827 |
| 1.0477 | 22.5 | 1.75895 | 84.93517 | 27.45242 |
| 1.0603 | 16.9 | 1.8923 | 106.4808 | 29.7366 |
| 1.0387 | 26.6 | 1.88595 | 99.45013 | 27.9605 |
| 1.1089 | 0 | 1.7272 | 53.7507 | 18.01768 |
| 1.0725 | 11.5 | 1.70815 | 66.11109 | 22.65804 |
| 1.0713 | 12.1 | 1.77165 | 72.23458 | 23.01385 |
| 1.0587 | 17.5 | 1.88595 | 77.3375 | 21.74352 |
| 1.0794 | 8.6 | 1.8161 | 75.97672 | 23.03568 |
| 1.0453 | 23.6 | 1.88595 | 105.5736 | 29.68212 |
| 1.0524 | 20.4 | 1.8288 | 95.48119 | 28.54864 |
| 1.052 | 20.5 | 1.8415 | 91.73906 | 27.05271 |
| 1.0434 | 24.4 | 1.73355 | 83.91459 | 27.92317 |
| 1.0728 | 11.4 | 1.75895 | 69.39963 | 22.43108 |
| 1.014 | 38.1 | 1.9304 | 110.7899 | 29.73073 |
| 1.0624 | 15.9 | 1.7907 | 87.77012 | 27.37165 |
| 1.0429 | 24.7 | 1.89865 | 101.9449 | 28.27976 |
| 1.047 | 22.8 | 1.84785 | 73.82216 | 21.61988 |
| 1.0411 | 25.5 | 1.73355 | 81.64663 | 27.16849 |
| 1.0488 | 22 | 1.7526 | 70.87381 | 23.07386 |
| 1.0583 | 17.7 | 1.8161 | 76.20352 | 23.10444 |
| 1.0841 | 6.6 | 1.84785 | 75.86332 | 22.21767 |
| 1.0462 | 23.6 | 1.7145 | 77.4509 | 26.34823 |
| 1.0709 | 12.2 | 1.78435 | 80.85284 | 25.39424 |
| 1.0484 | 22.1 | 1.75895 | 68.03886 | 21.99126 |
| 1.034 | 28.7 | 1.8161 | 90.94527 | 27.57405 |
| 1.0854 | 6 | 1.8796 | 83.461 | 23.62396 |
| 1.0209 | 34.8 | 1.77165 | 101.1511 | 32.22662 |
| 1.061 | 16.6 | 1.8542 | 94.68741 | 27.54096 |
| 1.025 | 32.9 | 1.6637 | 75.29633 | 27.20344 |
| 1.0254 | 32.8 | 1.8415 | 88.45051 | 26.08296 |
| 1.0771 | 9.6 | 1.78435 | 72.80158 | 22.8655 |
| 1.0742 | 10.8 | 1.79705 | 72.46138 | 22.43811 |
| 1.0829 | 7.1 | 1.7272 | 63.72973 | 21.36273 |
| 1.0373 | 27.2 | 1.8923 | 98.08935 | 27.39314 |
| 1.0543 | 19.5 | 1.82245 | 76.31692 | 22.97786 |
| 1.0561 | 18.7 | 1.79705 | 88.33711 | 27.35413 |
| 1.0543 | 19.5 | 1.8542 | 78.35808 | 22.79138 |
| 1.0678 | 13.6 | 1.77165 | 67.69866 | 21.56871 |
| 1.0819 | 7.5 | 1.778 | 70.08002 | 22.16821 |
| 1.0433 | 24.5 | 1.82245 | 90.37828 | 27.21152 |
| 1.0646 | 15 | 1.75895 | 70.08002 | 22.65099 |
| 1.0706 | 12.4 | 1.7907 | 69.51303 | 21.67807 |
| 1.0399 | 26 | 1.83515 | 104.3262 | 30.97778 |
| 1.0726 | 11.5 | 1.7145 | 73.36857 | 24.95945 |
| 1.0874 | 5.2 | 1.70815 | 64.52351 | 22.11393 |
| 1.074 | 10.9 | 1.74625 | 81.53323 | 26.73756 |
| 1.0703 | 12.5 | 1.69545 | 57.37943 | 19.96118 |
| 1.065 | 14.8 | 1.73355 | 76.88391 | 25.58366 |
| 1.0418 | 25.2 | 1.88595 | 90.03809 | 25.3143 |
| 1.0647 | 14.9 | 1.7653 | 79.15187 | 25.39944 |
| 1.0601 | 17 | 1.7399 | 76.09012 | 25.13505 |
| 1.0745 | 10.6 | 1.67005 | 67.01827 | 24.02892 |
| 1.062 | 16.1 | 1.82245 | 82.66721 | 24.88984 |
| 1.0636 | 15.4 | 1.8161 | 79.60546 | 24.13589 |
| 1.0384 | 26.7 | 1.70815 | 73.36857 | 25.14537 |
| 1.0403 | 25.8 | 1.7145 | 71.5542 | 24.34222 |
| 1.0563 | 18.6 | 1.7145 | 76.54371 | 26.03961 |
| 1.0424 | 24.8 | 1.83515 | 86.86294 | 25.79238 |
| 1.0372 | 27.3 | 1.7653 | 99.40477 | 31.89849 |
| 1.0705 | 12.4 | 1.7653 | 70.42022 | 22.5975 |
| 1.0316 | 29.9 | 1.67005 | 86.06915 | 30.85948 |
| 1.0599 | 17 | 1.67005 | 57.83303 | 20.73562 |
| 1.0207 | 35 | 1.73355 | 101.8315 | 33.88515 |
| 1.0304 | 30.4 | 1.8288 | 106.254 | 31.76968 |
| 1.0256 | 32.6 | 1.84785 | 103.3057 | 30.25456 |
| 1.0334 | 29 | 1.7399 | 90.49168 | 29.89235 |
| 1.0641 | 15.2 | 1.75895 | 70.53361 | 22.7976 |
| 1.0308 | 30.2 | 1.7907 | 97.74916 | 30.48368 |
| 1.0736 | 11 | 1.7018 | 60.89478 | 21.02631 |
| 1.0236 | 33.6 | 1.77165 | 91.17207 | 29.04731 |
| 1.0328 | 29.3 | 1.6764 | 84.70838 | 30.14193 |
| 1.0399 | 26 | 1.7907 | 86.52274 | 26.98265 |
| 1.0271 | 31.9 | 1.778 | 94.12042 | 29.77285 |
Exploratory data analyses (EDA)
Before we run any quantitative tests, let’s examine what these variables look like in graphical form. Keep an eye out for which variables appear to follow a normal distribution.
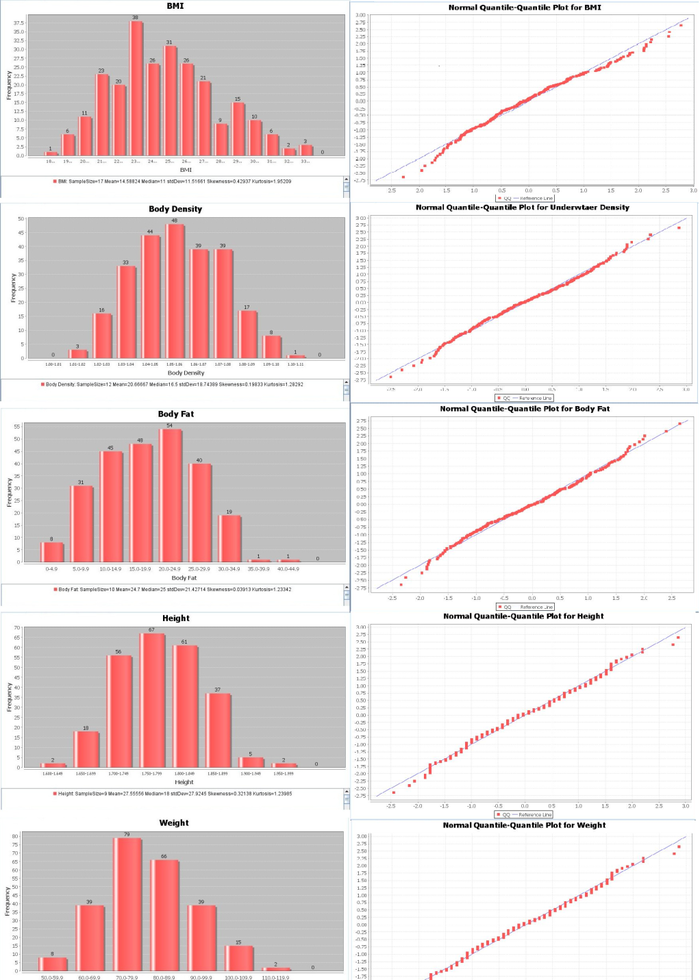
Quantitative Data Analyses (QDA)
In this section, we will be testing the BMI variable for normality, although the same analysis can be carried for the other variables. As the name goodness-of-fit implies, we first need to create a normal model to compare to. We will use the sample mean (25.18643319) and standard deviation (3.146481308) as the parameters of the normal distribution.
The next few steps will use the SOCR Distributions Applet (see Distribution Activities). Open the applet in a java-enabled browser.
Data Modeling
Enter in the values for the mean and standard deviation, then drag the graph down to see your full distribution.
To run a goodness of fit test, we will need to create a set of bins to compare between the real distribution and the expected normal one. For simplicity’s sake, we will use a 16 bins of bin-size 1 beginning with BMI=18 and ending with BMI=34. To find the frequency of results in each bin from the normal distribution, click on the edges of the bin size (try to be as accurate as possible) on the normal distribution applet. The example shown alternatively, use the normal CDF function.
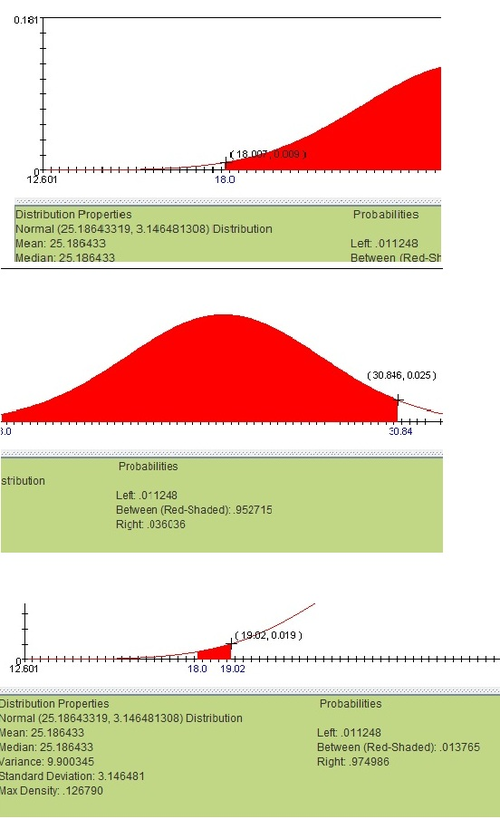
After calculating the probability of each bin, multiply each of these probabilities by the total number of cases (in this case, 248). Now we can place these calculated frequencies next to the frequencies from the observed distribution (the observed frequencies were found by plain counting):
| Bin(Simplified) | Bin(Actual) | Normal_Probability | EstimatedNormalFrequency | ObservedFrequency |
|---|---|---|---|---|
| 18-19 | 18.000-18.999 | 0.013454035 | 3.39041682 | 1 |
| 19-20 | 19.000-19.999 | 0.025001757 | 6.300442764 | 6 |
| 20-21 | 20.000-20.999 | 0.042032155 | 10.59210306 | 11 |
| 21-22 | 21.000-21.999 | 0.06392769 | 16.10977788 | 23 |
| 22-23 | 22.000-22.999 | 0.087962245 | 22.16648574 | 20 |
| 23-24 | 23.000-23.999 | 0.109497598 | 27.5933947 | 38 |
| 24-25 | 24.000-24.999 | 0.123313845 | 31.07508894 | 26 |
| 25-26 | 25.000-25.999 | 0.125638222 | 31.66083194 | 31 |
| 26-27 | 26.000-26.999 | 0.115806485 | 29.18323422 | 26 |
| 27-28 | 27.000-27.999 | 0.096570457 | 24.33575516 | 21 |
| 28-29 | 28.000-28.999 | 0.072854419 | 18.35931359 | 9 |
| 29-30 | 29.000-29.999 | 0.049724263 | 12.53051428 | 15 |
| 30-31 | 30.000-30.999 | 0.030702836 | 7.737114672 | 10 |
| 31-32 | 31.000-31.999 | 0.017150734 | 4.321984968 | 6 |
| 32-33 | 32.000-32.999 | 0.008667207 | 2.184136164 | 2 |
| 33-34 | 33.000-33.999 | 0.00396249 | 0.99854748 | 3 |
It might be useful to see how this hypothetical expected data matches up with our actual results graphically. Note the differences between the two data sets in the Quantile-Quantile Charts (ignore the stacked shape of the normal estimation, which is due to binning the data). Note that the line is a better fit in the latter case).
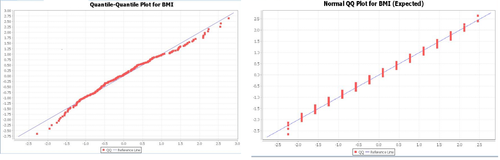
Chi-Square Goodness-of-Fit Test
With these values now settled, we can begin the Chi-square analysis. Open up the SOCR Analyses Applet in a Java-enabled browser, and then select the Chi-square Goodness of Fit in the pull-down menu on the left:
Next, enter the data into two columns using the Paste button.
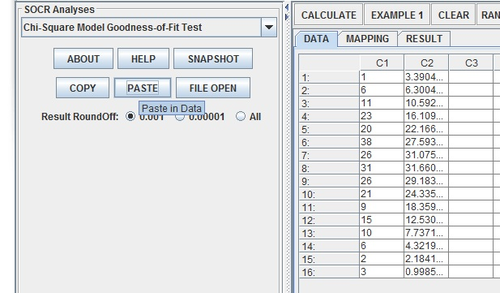
Name the two columns Observed (for the actual results) and Expected (for the normal model estimates).
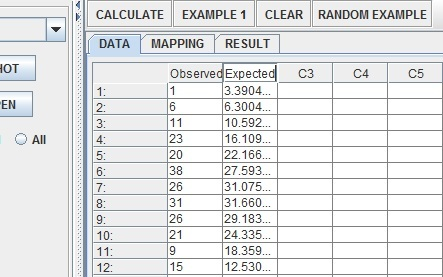
Click on the Mapping tab and add observed and expected into the correct bins.
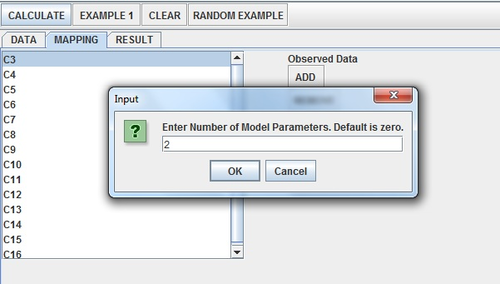
Click the Calculate Button. A window should pop up asking about the number of parameters. Recall that the normal distribution is defined by two parameters—mean and standard deviation. Enter “2” and press “OK”.
The results page should come up with the following text:
- Observed Data = Observed
- Expected Data = Expected
Chi-Square Goodness of Fit Results:
- Total Counts = 16
- Number of Parameters = 2
- Chi-Square Goodness of Fit Results:
- ********** Chi-Square Statistic is: 21.044 *********
- ********** Chi-Square Degrees of Freedom is: 16 - 2 - 1 = 13 *********
- ********** Chi-Square p-value is: .072 *********
Based on α = 0.05, there is not enough evidence to conclude that the BMI data distribution does not fit a normal distribution. However, it is worth noting that it does come very close. This understanding of a distribution is very important to health officials; for example, it helps creates the charts that doctors national-wide use to understand. In addition, a deviation from that distribution can be used to chart changes in the overall health of the nation (Penman, 2006).
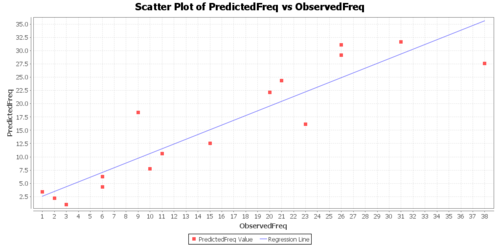
Linear Regression
Finally, we can explore the correlation between the observed frequencies and the prediction-model values (predicted frequencies) of the BMI data within each of the 16 bins. If there is a good agreement (e.g., high correlation) this would indicate that the normal distribution model fits well the observed data (BMI frequencies).
Copy and paste the 2 column data (observed and predicted frequencies) into the Simple Linear Regression applet of SOCR Analysis.
Map the predicted and observed frequencies to the Dependent and Independent variables (Mapping Tab).
Click Calculate button to view the results. Regression Model:
- PredictedFreq = 1.71070 + 0.8918062570205698 * ObservedFreq
- Correlation(ObservedFreq, PredictedFreq) = .91394
- R-Square = .83529
- Intercept:
- Parameter Estimate: 1.71070
- Standard Error: 2.00468
- T-Statistics: .85335
- P-Value: .40783
- Slope:
- Parameter Estimate: .89181
- Standard Error: .10584
- T-Statistics: 8.42598
- P-Value: .00000
Regression Graphs
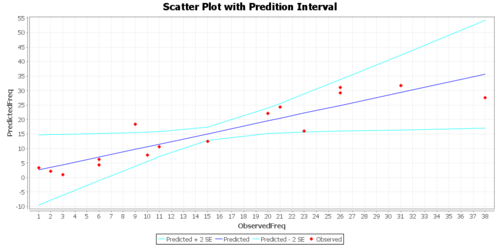
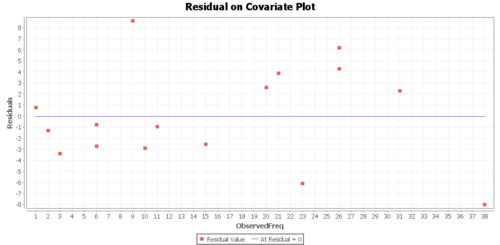
The Graphs tab includes a regression model plot, scatter plot with confidence/prediction limits, and various plots of the residuals.
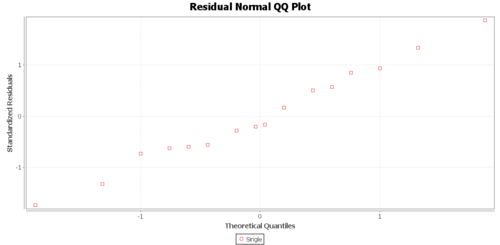
Practice problems
- Try this method out on one of the other variables. See if it breaks from the normal distribution.
- Many biological measures are said to follow a normal distribution. Look under the data header “Biomedical Data” in the SOCR Free Datasets and check this claim out with one of the variables you are interested in.
See also
References
- K.W. Penrose, A.G. Nelson, A.G. Fisher, FACSM, Human Performance Research Center, Brigham Young University, Provo, Utah 84602 as listed in Medicine and Science in Sports and Exercise, vol. 17, no. 2, April 1985, p. 189.
- A.D. Penman and W.D. Johnson. Changing shape of the body mass index distribution curve in the population: implications for public health policy to reduce the prevalence of adult obesity, Preventing chronic disease, vol. 3, no. 2, 2006.
Translate this page:
