SOCR EduMaterials Activities Binomial Distributions
From Socr
This is an activity to explore the Binomial, Geometric, and Hypergeometric Probability Distributions.
- Description: You can access the applets for the above distributions at http://www.socr.ucla.edu/htmls/SOCR_Distributions.html .
- Exercise 1: Use SOCR to graph and print the following distributions and answer the questions below. Also, comment on the shape of each one of these distributions:
- a.
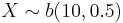 , find P(X = 3), E(X), sd(X), and verify them with the formulas discussed in class.
, find P(X = 3), E(X), sd(X), and verify them with the formulas discussed in class.
- b.
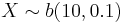 , find
, find 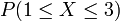 .
.
- c.
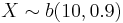 , find
, find 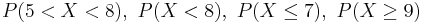 .
.
- d.
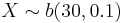 , find P(X > 2).
, find P(X > 2).
- a.
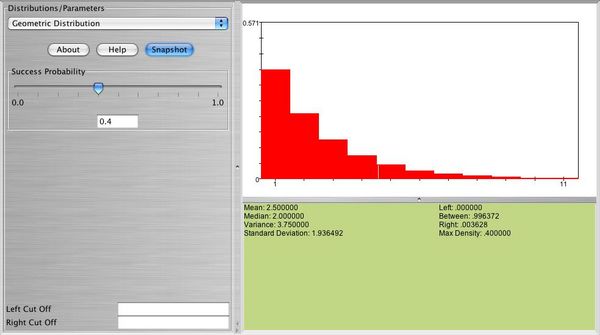
Below you can see a snapshot of the distribution of 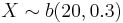
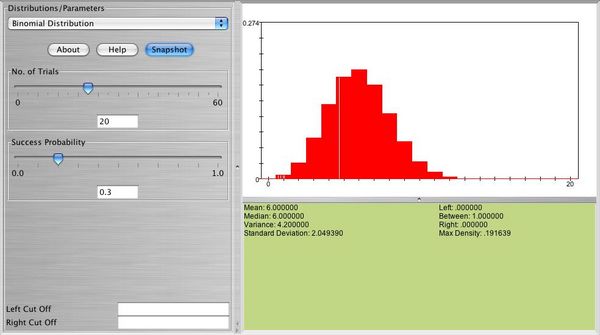
- Exercise 2: Use SOCR to graph and print the distribution of a geometric random variable with p = 0.2,p = 0.7. What is the shape of these distributions? What happens when p is large? What happens when p is small?
Below you can see a snapshot of the distribution of 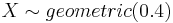
- Exercise 3: Select the geometric probability distribution with p = 0.2. Use SOCR to compute the following:
- a. P(X = 5)
- b. P(X > 3)
- c.
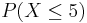
- d. P(X > 6)
- e.
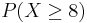
- f.
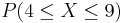
- g. P(4 < X < 9)
- Exercise 4: Verify that your answers in exercise 3 agree with the formulas discussed in class, for example, P(X = x) = (1 − p)x − 1p, P(X > k) = (1 − p)k, etc. Write all your answers in detail using those formulas.
- Exercise 5: Let X follow the hypergeometric probability distribution with N = 52, n = 10, and number of "hot" items 13. Use SOCR to graph and print this distribution.
Below you can see a snapshot of the distribution of 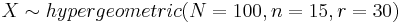
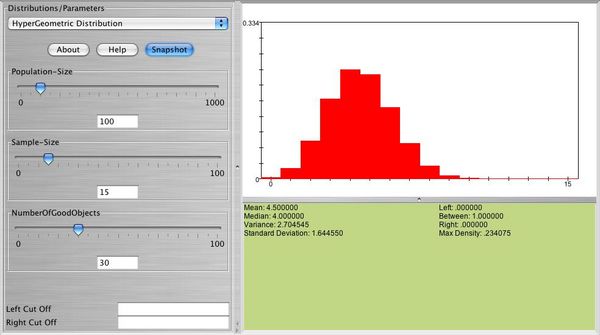
- Exercise 6: Refer to exercise 5. Use SOCR to compute P(X = 5) and write down the formula that gives this answer.
- Exercise 7: Binomial approximation to hypergeometric: Let X follow the hypergeometric probability distribution with
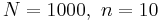 and number of "hot" items 50. Graph and print this distribution.
and number of "hot" items 50. Graph and print this distribution.
- Exercise 8: Refer to exercise 7. Use SOCR to compute the exact probability: P(X = 2). Approximate P(X = 2) using the binomial distribution. Is the approximation good? Why?
- Exercise 9: Do you think you can approximate well the hypergeometric probability distribution with
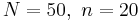 , and number of "hot" items 40 using the binomial probability distribution? Graph and print the exact (hypergeometric) and the approximate (binomial) distributions and compare.
, and number of "hot" items 40 using the binomial probability distribution? Graph and print the exact (hypergeometric) and the approximate (binomial) distributions and compare.
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:
