SOCR EduMaterials Activities BuffonCoinExperiment
From Socr
Contents |
Buffon Coin Experiment
Description
The Buffon Coin Experiment is a general example that demonstrates the properties of calculus based probability by tossing a coin on a floor with square tiles.
In the first table, the center (X,Y) of the coin relative to the center of the square and variable I are recorded on each update where I indicates the event that the coin crosses a crack. In the second table, the numerical values of the density of I and the empirical density of I are recorded.
The tossing of a coin is shown graphically in the first picture box. In the scatter plot, the center (X,Y) of the coin is shown graphically as a red dot. In the last graph, the density of I is shown in blue and the empirical density of I is shown in red.
The parameter of the process is the radius r of the coin, and can be modified with the scroll bar.
Goal
To provide a simulation that describes the probability of two variables—in this case, the center (X,Y) of the coin relative to the center of the square and the event that the coin crosses a crack. The Buffon Coin Experiment will provide better understanding of calculus based probability.
Experiments
Go to the SOCR Experiment [[1]] and select the Buffon Coin Experiment from the drop-down list of experiments on the top left. The image below shows the initial view of this experiment:
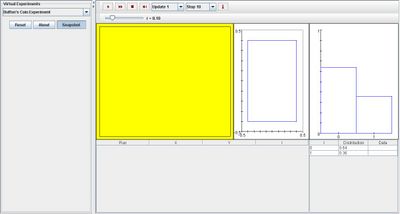
When pressing the play button, one trial will be executed and recorded in the distribution table below. The fast forward button symbolizes the nth number of trials to be executed each time. The stop button ceases any activity and is helpful when the experimenter chooses “continuous,” indicating an infinite number of events. The fourth button will reset the entire experiment, deleting all previous information and data collected. The “update” scroll indicates nth number of trials (1, 10, 100, or 1000) performed when selecting the fast forward button and the “stop” scroll indicates the maximum number of trials in the experiment.
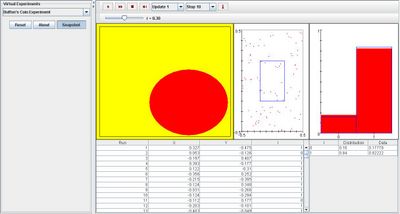
When parameter r is increased, the blue graph in the scatter plot minimizes to show that the probability the needle will land inside the square tile decreases. In the distribution graph, the density of I displays a higher chance for the needle to cross a crack. This is valid since the radius of the coin has increased. The image below illustrates this event:
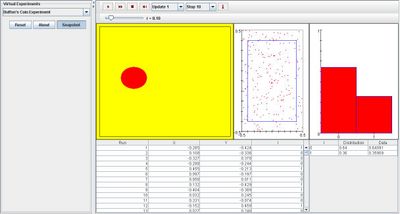
When parameter r obtains a small value, the distribution graph displays a higher chance for the needle to stay within the boundaries of the tile. The scatter plot shows that it is more likely for the needle to land within the square tile than crossing a crack. Note that the scatter plot proves random sampling since there are no visible patterns on each trial. The image below displays an event in which r has a small value:
Applications
The Buffon’s Coin Experiment uses calculus to generalize outcomes of different types of probability.
This type of experiment may also be used in regular activities such as carnival games where the player must toss a coin and land within an image on the flat surface in front of them. If the coin lands within the image, the player wins; if the coin lands outside of the image—crossing a crack—the player loses. Using the Buffon’s Coin Experiment can generalize this game when the player is not allowed to see where he tosses (e.g. blind folded, turned around, etc.) so that all the tosses are thrown at random.
Suppose a student randomly selects an ad on a website but he already knows that the ads on the right are school-related. He wants to determine the probability of selecting an adverstisement from a local company. By using the Buffon Coin's Experiment, he lets the tile represent all of the ads except the ones on the right so landing outside of the tile calculates the probability of clicking on a school-related advertisement. In this applet, the coin landing on the crack represents the probability he will click on a desirable advertisement. After many runs, the student will determine his probability of selecting an ad of interest.
Translate this page:
