SOCR EduMaterials Activities CentralLimitTheorem
From Socr
This is an activity to explore the distribution of the sample mean and the Central Limit Theorem (CLT).
- Description: You can access the applet for the Sample Mean Experiment at SOCR Experiments.
The central limit theorem (clt) states that if a random sample of size n (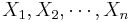 ) is selected from ANY distribution (this distribution has mean μ and standard deviation σ), then the sample mean
) is selected from ANY distribution (this distribution has mean μ and standard deviation σ), then the sample mean 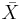 approximately follows the normal distribution with mean μ and standard deviation
approximately follows the normal distribution with mean μ and standard deviation 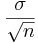 . Requirements: Large n, usually
. Requirements: Large n, usually 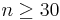 , and independent observations. Note: If the sample is selected from a population that it is already normal then n can be of any size (as small as n = 2). We can illustrate the clt using some experiments in SOCR. You can find the Sample Mean Experiment under Experiments in SOCR.
, and independent observations. Note: If the sample is selected from a population that it is already normal then n can be of any size (as small as n = 2). We can illustrate the clt using some experiments in SOCR. You can find the Sample Mean Experiment under Experiments in SOCR.
Answer the following questions:
- Exercise 1:
- a. Select as population the normal distribution with μ = 5,σ = 2. You will randomly select many samples of size N = 16 each. The two distributions in blue are the theoretical distributions of X (on the left), and
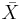 on the right labeled with M. Explain what the numbers below X, and below
on the right labeled with M. Explain what the numbers below X, and below 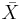 are and what the column next to each one represents.
are and what the column next to each one represents.
- b. One of the numbers under the column of X is 3.16. How many standard deviations this number is from the mean of X (μ = 5), and what is P(3.16 < X < 5)? Use the z score and your z table or SOCR (you will need to click on distributions and select the normal distribution with μ = 5,σ = 2).
- c. One of the numbers under the column of
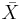 is 3.14. How many standard deviations this number is from the mean of
is 3.14. How many standard deviations this number is from the mean of 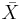 (μ = 5), and what is
(μ = 5), and what is 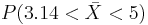 ? Use the z score and your z table or SOCR (you will need to click on distributions and select the normal distribution with
? Use the z score and your z table or SOCR (you will need to click on distributions and select the normal distribution with 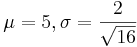 ).
).
- d. Explain the difference between parts (b) and (c). Draw by hand the two distributions (X, and
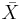 ) and show the probabilities of parts (b) and (c) on the graphs (draw first the distribution of X and below it the distribution of
) and show the probabilities of parts (b) and (c) on the graphs (draw first the distribution of X and below it the distribution of 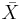 ).
).
- e. Perform the experiment 1000 times (μ = 5,σ = 2,N = 16). Take a snapshot of the output. What do you observe? What is the mean of these 1000 sample means? What is the standard deviation of these 1000 sample means? How well do they compare to the theoretical mean and standard deviation of
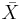 ?
?
- f. In theory the sample size N has to be large (at least 30) to get normal distribution of the sample mean. In part (e) we have only selected samples of size N = 16. Is there a problem here?
- a. Select as population the normal distribution with μ = 5,σ = 2. You will randomly select many samples of size N = 16 each. The two distributions in blue are the theoretical distributions of X (on the left), and
- Exercise 2:
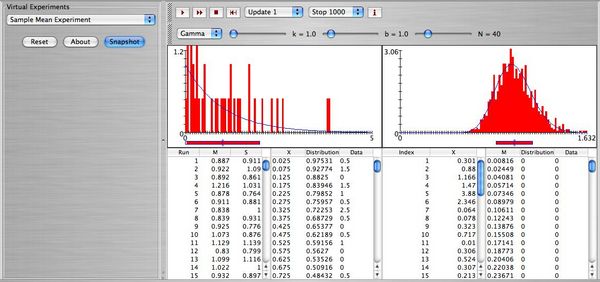
- a. Select as population the gamma distribution with k = 1,b = 1 (this is a skewed to the right distribution with mean μ = 1 and standard deviation σ = 1). You will select samples of size N = 16. The two distributions in blue are the theoretical distributions of X and
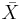 . What is the shape of the distribution of
. What is the shape of the distribution of 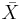 ?
?
- b. Perform the experiment 1000 times. Take a snapshot of the output and comment?
- c. Decrease the sample size to N = 1. What do you observe? Explain. What do you think needs to be done so that the sample mean is approximately normal.
- d. Increase the sample to N = 36. Describe the distribution of the sample mean? Run the experiment 1000 times. What is the mean of these 1000 sample means? What is the standard deviation of these 1000 sample means? How well do they compare to the theoretical mean and standard deviation
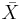 ?
?
- a. Select as population the gamma distribution with k = 1,b = 1 (this is a skewed to the right distribution with mean μ = 1 and standard deviation σ = 1). You will select samples of size N = 16. The two distributions in blue are the theoretical distributions of X and
- Exercise 3:
- a. Choose as population the binomial distribution with number of trials n = 4 and probability of success p = 0.9. Select samples of size N = 2. Describe the distribution of the sample mean
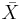 . What is the shape of X? What is the shape of
. What is the shape of X? What is the shape of 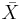 ?
?
- b. Increase the sample size to N = 31. Describe the distribution of
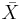 . What is the shape of the distribution of
. What is the shape of the distribution of 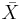 ?
?
- c. Run the experiment 1000 times (
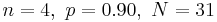 ). What is the mean of these 1000 sample means? What is the standard deviation of these 1000 sample means? How well do they compare to the theoretical mean and standard deviation
). What is the mean of these 1000 sample means? What is the standard deviation of these 1000 sample means? How well do they compare to the theoretical mean and standard deviation 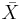 ?
?
- a. Choose as population the binomial distribution with number of trials n = 4 and probability of success p = 0.9. Select samples of size N = 2. Describe the distribution of the sample mean
Below you can see a snapshot of the theoretical distribution of 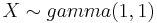 and
and 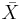 , together with the simulation results of 1000 samples from the gamma distribution when the sample size is 40.
, together with the simulation results of 1000 samples from the gamma distribution when the sample size is 40.
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:
