SOCR EduMaterials Activities Central Limit Theorem Chi square examples

From Socr

(Difference between revisions)
Jump to: navigation, search
Line 1: Line 1:
 +
*'''Answer:'''
 +
*a. false, the standard deviation of the sample mean is <math>\frac{\sigma}{\sqrt n}</math>. Thus as the sample size increases, n increases, and as n increases, the standard deviation decreases.
 +
*b. True
 +
*c. False, standard deviation of the sample mean is <math>\frac{\sigma}{\sqrt n}</math>
 +
*d. True, the standard deviation of the total of a sample of n observations is <math>n\sqrt \sigma</math>; but the standard deviation of the sample mean is <math>\frac{\sigma}{\sqrt n}.</math>Unless n is one, the standard deviation of the total of a sample of n observations exceeds the standard deviation of the sample mean.
 +
*e. False, let's assume <math>\sigma=2</math> and <math>n=2</math>. In this case, the z-score for <math>P(\overline{X} > 4)</math> would be -2.828 while the z-score for <math>P(X>4)</math> would be -2.  <math>P(Z>-2.828) > P(Z>-2) </math>. Therefore the statement is false.
 +
 +
*'''Answer:'''
 +
*a. <math>P(X \ge 1000)= P(X=1000)+P(X=1001)+....+P(X=1500)= (1500 \choose 1000) \times (.7)^1000 \times (.3)^500 + (1500 \choose 1001) \times (.7)^1001 \times (.3)^499 + ...+(1500 \choose 1500) \times (.7)^1500 \times (.3)^0 = \summation (\1500 \choose X) \times (.7)^X \times (.3)^1500-X</math>
 +
*b. We can use the normal approximation to binomial: <math>\mu = np = 1500 \times 0.70 = 1050.</math> and <math>\sigma =
 +
\sqrt npq = \sqrt1500 \times 0.7 \times 0.3= 17.748.</math>
 +
<math>P(X \ge 1000)= P(Z> \frac{999.5-1050}{17.748}=P(Z>-2.845)=.9977</math>
 +
* Below you can see a snapshot for this approximation:
 +
<center>[[Image: SOCR_Activities_CLT_Christou_example2.jpg|600px]]</center>
 +
*'''Answer:'''
 +
*a. <math>\overline{X} \sim N(8, \frac{20}{\sqrt400}). P(\overline{X} <6.50) =P(Z<-1.5)=.0667</math>
 +
*Below you can see a snapshot for this part:
 +
<center>[[Image: SOCR_Activities_CLT_Christou_example3_a.jpg|600px]]</center>
 +
*b. ??
 +
*c. The central limit theorem states that the sample mean approaches the normal distribution as the sample size gets bigger. Usually, if <math> n \ge 30</math>we can assume that the sample mean approaches the normal distribution. In this case <math>n=400</math>. Therefore n satisfies the requirement of a large n. 
 +
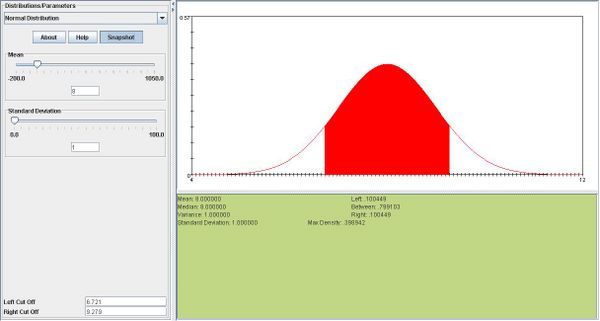
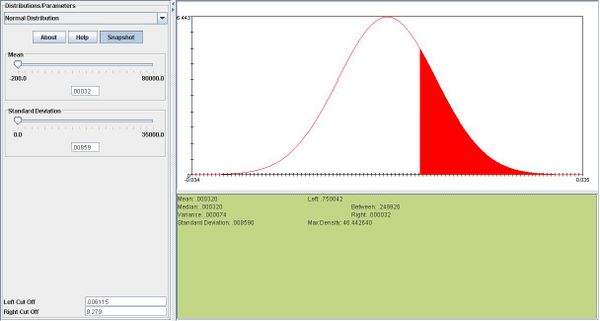
*d.<math>\overline{X} \sim N(8,1).</math>According to the snapshot below, the middle 80% of this distribution is (6.721,9.279). Therefore <math>w=8-6.721 =1.29</math>
 +
<center>[[Image: SOCR_Activities_Normal_Christou_example3_d.jpg|600px]]</center>
 +
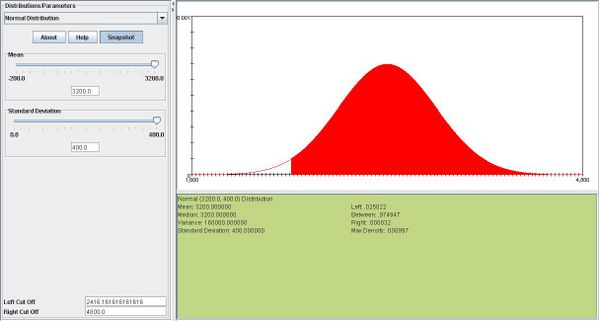
*e. <math>T \sim N(n\mu,\sigma\sqrt n).</math> In this case, <math>T \sim N(3200,400).</math> We know that  <math>P(T>b) =.975.</math>So now we need to find the 97.5th percentile of this distribution using SOCR. According to the SOCR snapshot below, the 97.5th percentile of this distribution is 3984. Therefore b=3984.
 +
<center>[[Image: SOCR_Activities_Normal_Christou_example3_e.jpg|600px]]</center>
 +
*'''Answer:'''
 +
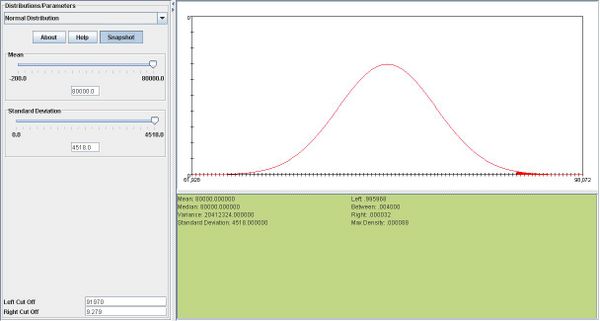
*a. <math>\overline{X} \sim N(\mu, \frac{\sigma}{\sqrt n }</math>. In this case, <math>\overline{X} \sim N(80000, 4518.48)</math>.
 +
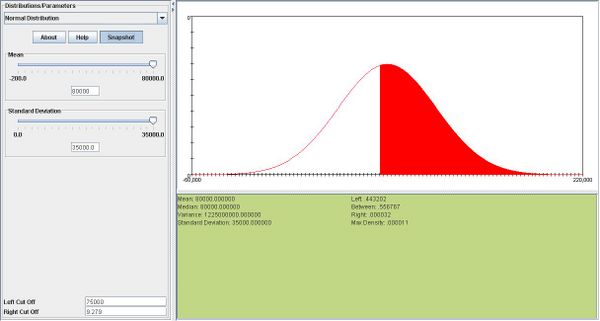
*b. We can find the answer using SOCR. The answer is 0.004032. Please see snapshot below:
 +
<center>[[Image: SOCR_Activities_Normal_Christou_example4_.jpg|600px]]</center>
 +
*c. We can find the answer right away using SOCR. Please see snapshots below:
 +
<center>This is the distribution for <math>X</math></center>
 +
<center>[[Image: SOCR_Activities_Normal_Christou_example4_c.jpg|600px]]</center>
 +
<center>This is the distribution for <math>\overline{X}</math></center>
 +
<center>[[Image: SOCR_Activities_Normal_Christou_example3_c2.jpg|600px]]</center>
 +
*The probabilities are 55.6% for  one hour vs. 86.6% for sample mean. Therefore the sample mean is more likely to be greater than 75000 hours.
 +
 +
*'''Answer:'''
 +
*a. According to the SOCR snapshot below, the 75th percentile is 0.006115.
 +
<center>[[Image: SOCR_Activities_Normal_Christou_example5_aa.jpg|600px]]</center>
 +
*b.<math>P(X>.01)=.13.</math>We can see this in the snapshot below:
 +
<center>[[Image: SOCR_Activities_Normal_Christou_example5_bb.jpg|600px]]</center>
 +
<math>P(R=2)=5 \choose 2 \times .13^2 \times .87^3 = 0.11128.
 +
<center>[[Image: SOCR_Activities_Normal_Christou_example5_bc.jpg|600px]]</center>
 +
*c. i. <math>X \sim N(.00032,.00192)
 +
    ii. .0074
 +
<center>[[Image: SOCR_Activities_Normal_Christou_example5_cc_ii.jpg|600px]]</center>
 +
    iii.One day's return is more likely to be greater than .007. 0.21 vs. .00022
 +
<center>This is the snapshot for <math>P(X>.007)</math></center>
 +
<center>[[Image: SOCR_Activities_Normal_Christou_example5_cc_iii_1.jpg|600px]]</center>
 +
<center>This is the snapshot for <math>P(\overline{X}>.007)</math></center>
 +
<center>[[Image: SOCR_Activities_Normal_Christou_example5_cc_iii_2.jpg|600px]]</center>
 +
 +
*'''Answer:'''

Revision as of 21:31, 14 May 2007

  • Answer:
  • a. false, the standard deviation of the sample mean is 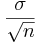\frac{\sigma}{\sqrt n}. Thus as the sample size increases, n increases, and as n increases, the standard deviation decreases.
  • b. True
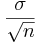
  • c. False, standard deviation of the sample mean is \frac{\sigma}{\sqrt n}
  • d. True, the standard deviation of the total of a sample of n observations is 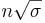n\sqrt \sigma; but the standard deviation of the sample mean is 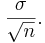\frac{\sigma}{\sqrt n}.Unless n is one, the standard deviation of the total of a sample of n observations exceeds the standard deviation of the sample mean.
  • e. False, let's assume σ = 2 and n = 2. In this case, the z-score for 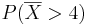P(\overline{X} > 4) would be -2.828 while the z-score for P(X > 4) would be -2. P(Z > − 2.828) > P(Z > − 2). Therefore the statement is false.
  • Answer:
  • a. Failed to parse (syntax error): P(X \ge 1000)= P(X=1000)+P(X=1001)+....+P(X=1500)= (1500 \choose 1000) \times (.7)^1000 \times (.3)^500 + (1500 \choose 1001) \times (.7)^1001 \times (.3)^499 + ...+(1500 \choose 1500) \times (.7)^1500 \times (.3)^0 = \summation (\1500 \choose X) \times (.7)^X \times (.3)^1500-X
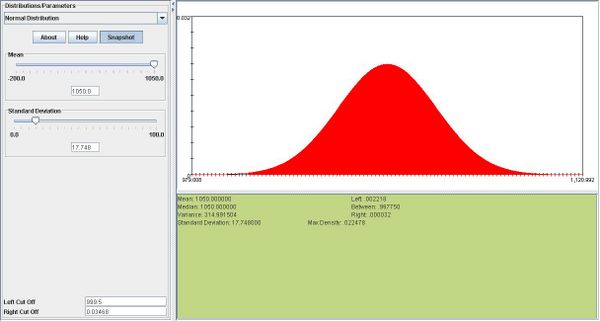
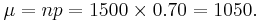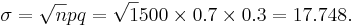
  • b. We can use the normal approximation to binomial: \mu = np = 1500 \times 0.70 = 1050. and \sigma = \sqrt npq = \sqrt1500 \times 0.7 \times 0.3= 17.748.

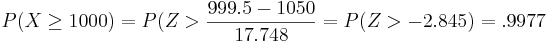
P(X \ge 1000)= P(Z> \frac{999.5-1050}{17.748}=P(Z>-2.845)=.9977

  • Below you can see a snapshot for this approximation:
  • Answer:
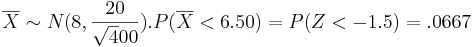
  • a. \overline{X} \sim N(8, \frac{20}{\sqrt400}). P(\overline{X} <6.50) =P(Z<-1.5)=.0667
  • Below you can see a snapshot for this part:
  • b. ??
  • c. The central limit theorem states that the sample mean approaches the normal distribution as the sample size gets bigger. Usually, if 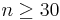n \ge 30we can assume that the sample mean approaches the normal distribution. In this case n = 400. Therefore n satisfies the requirement of a large n.
  • d.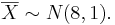\overline{X} \sim N(8,1).According to the snapshot below, the middle 80% of this distribution is (6.721,9.279). Therefore w = 8 − 6.721 = 1.29
  • e. 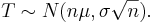T \sim N(n\mu,\sigma\sqrt n). In this case, 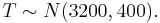T \sim N(3200,400). We know that P(T > b) = .975.So now we need to find the 97.5th percentile of this distribution using SOCR. According to the SOCR snapshot below, the 97.5th percentile of this distribution is 3984. Therefore b=3984.
  • Answer:
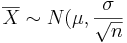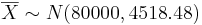  • a. \overline{X} \sim N(\mu, \frac{\sigma}{\sqrt n }. In this case, \overline{X} \sim N(80000, 4518.48).
  • b. We can find the answer using SOCR. The answer is 0.004032. Please see snapshot below:
  • c. We can find the answer right away using SOCR. Please see snapshots below:
This is the distribution for X
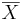
This is the distribution for \overline{X}
  • The probabilities are 55.6% for one hour vs. 86.6% for sample mean. Therefore the sample mean is more likely to be greater than 75000 hours.
  • Answer:
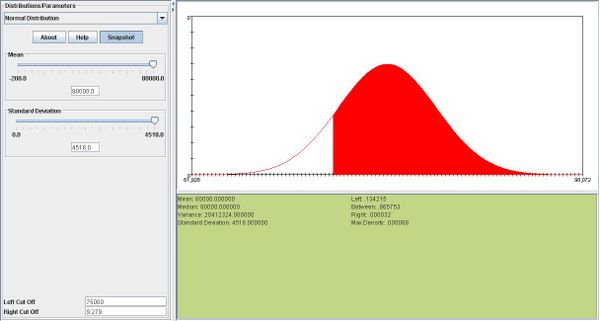
  • a. According to the SOCR snapshot below, the 75th percentile is 0.006115.
  • b.P(X > .01) = .13.We can see this in the snapshot below:

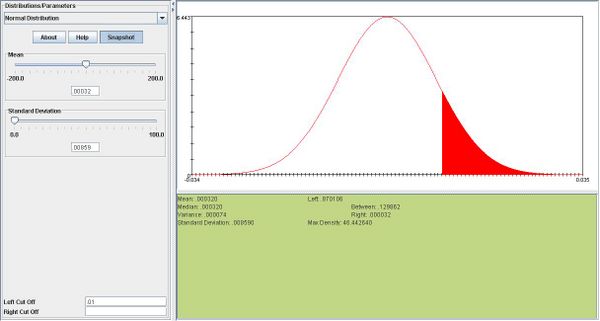
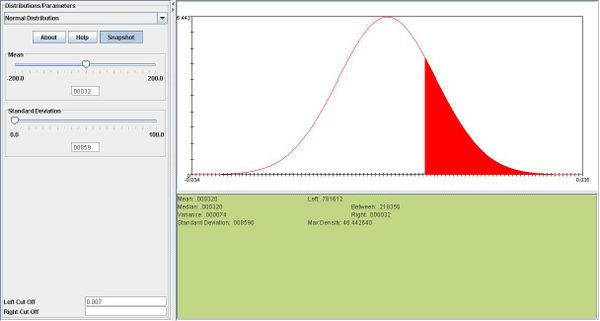
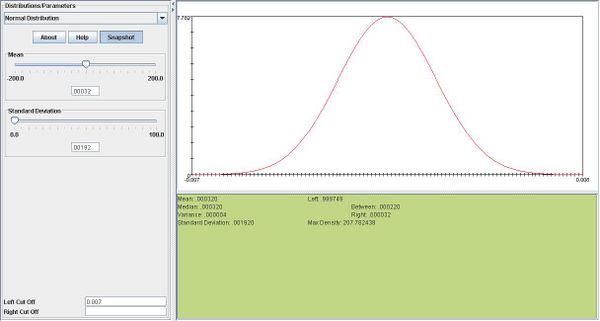
P(R=2)=5 \choose 2 \times .13^2 \times .87^3 = 0.11128. <center>[[Image: SOCR_Activities_Normal_Christou_example5_bc.jpg|600px]]</center> *c. i. <math>X \sim N(.00032,.00192) ii. .0074 <center>[[Image: SOCR_Activities_Normal_Christou_example5_cc_ii.jpg|600px]]</center> iii.One day's return is more likely to be greater than .007. 0.21 vs. .00022 <center>This is the snapshot for <math>P(X>.007)</center>

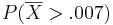
This is the snapshot for P(\overline{X}>.007)
  • Answer:
Retrieved from "http://wiki.stat.ucla.edu/socr/index.php/SOCR_EduMaterials_Activities_Central_Limit_Theorem_Chi_square_examples"
Personal tools