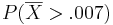SOCR EduMaterials Activities Central Limit Theorem Chi square examples
From Socr
(Difference between revisions)
Create90215 (Talk | contribs) |
Create90215 (Talk | contribs) |
||
| Line 1: | Line 1: | ||
| - | + | <center></center>'''Answer:''' | |
| - | + | <center></center>a. false, the standard deviation of the sample mean is <math>\frac{\sigma}{\sqrt n}</math>. Thus as the sample size increases, n increases, and as n increases, the standard deviation decreases. | |
| - | + | <center></center>b. True | |
| - | + | <center></center>c. False, standard deviation of the sample mean is <math>\frac{\sigma}{\sqrt n}</math> | |
| - | + | <center></center>d. True, the standard deviation of the total of a sample of n observations is <math>n\sqrt \sigma</math>; but the standard deviation of the sample mean is <math>\frac{\sigma}{\sqrt n}.</math>Unless n is one, the standard deviation of the total of a sample of n observations exceeds the standard deviation of the sample mean. | |
| - | + | <center></center>e. False, let's assume <math>\sigma=2</math> and <math>n=2</math>. In this case, the z-score for <math>P(\overline{X} > 4)</math> would be -2.828 while the z-score for <math>P(X>4)</math> would be -2. <math>P(Z>-2.828) > P(Z>-2) </math>. Therefore the statement is false. | |
| - | + | <center></center>'''Answer:''' | |
| - | + | <center></center>a. <math>P(X \ge 1000)= P(X=1000)+P(X=1001)+....+P(X=1500)= (1500 \choose 1000) \times (.7)^1000 \times (.3)^500 + (1500 \choose 1001) \times (.7)^1001 \times (.3)^499 + ...+(1500 \choose 1500) \times (.7)^1500 \times (.3)^0 = \summation (\1500 \choose X) \times (.7)^X \times (.3)^1500-X</math> | |
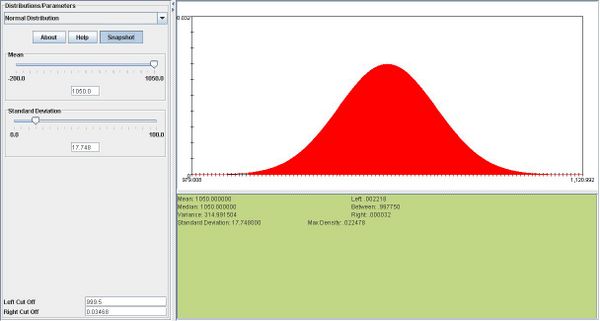
| - | + | <center></center>b. We can use the normal approximation to binomial: <math>\mu = np = 1500 \times 0.70 = 1050.</math> and <math>\sigma = | |
\sqrt npq = \sqrt1500 \times 0.7 \times 0.3= 17.748.</math> | \sqrt npq = \sqrt1500 \times 0.7 \times 0.3= 17.748.</math> | ||
<math>P(X \ge 1000)= P(Z> \frac{999.5-1050}{17.748}=P(Z>-2.845)=.9977</math> | <math>P(X \ge 1000)= P(Z> \frac{999.5-1050}{17.748}=P(Z>-2.845)=.9977</math> | ||
| - | + | <center></center> Below you can see a snapshot for this approximation: | |
<center>[[Image: SOCR_Activities_CLT_Christou_example2.jpg|600px]]</center> | <center>[[Image: SOCR_Activities_CLT_Christou_example2.jpg|600px]]</center> | ||
| - | + | <center></center>'''Answer:''' | |
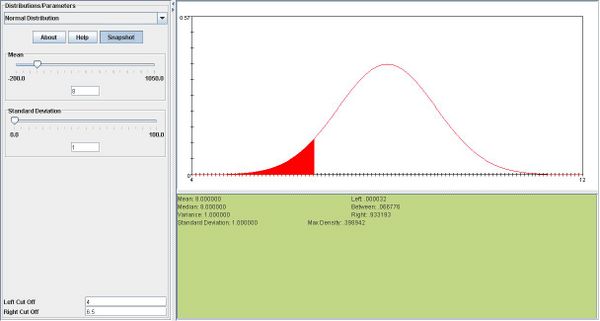
| - | + | <center></center>a. <math>\overline{X} \sim N(8, \frac{20}{\sqrt400}). P(\overline{X} <6.50) =P(Z<-1.5)=.0667</math> | |
| - | + | <center></center>Below you can see a snapshot for this part: | |
<center>[[Image: SOCR_Activities_CLT_Christou_example3_a.jpg|600px]]</center> | <center>[[Image: SOCR_Activities_CLT_Christou_example3_a.jpg|600px]]</center> | ||
| - | + | <center></center>b. ?? | |
| - | + | <center></center>c. The central limit theorem states that the sample mean approaches the normal distribution as the sample size gets bigger. Usually, if <math> n \ge 30</math> we can assume that the sample mean approaches the normal distribution. In this case <math>n=400</math>. Therefore n satisfies the requirement of a large n. | |
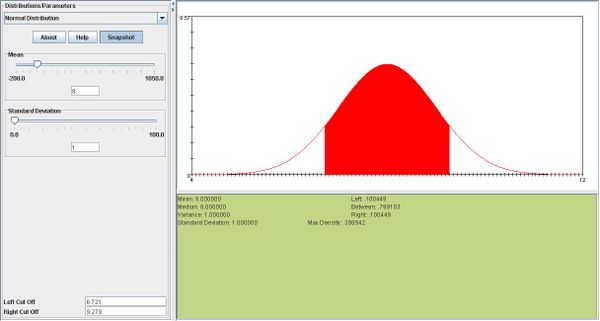
| - | + | <center></center>d.<math>\overline{X} \sim N(8,1).</math>According to the snapshot below, the middle 80% of this distribution is (6.721,9.279). Therefore <math>w=8-6.721 =1.29</math> | |
<center>[[Image: SOCR_Activities_Normal_Christou_example3_d.jpg|600px]]</center> | <center>[[Image: SOCR_Activities_Normal_Christou_example3_d.jpg|600px]]</center> | ||
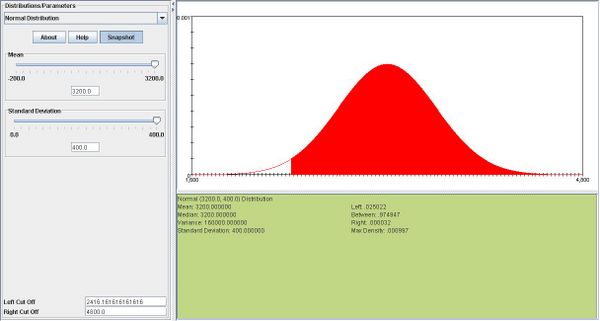
| - | + | <center></center>e. <math>T \sim N(n\mu,\sigma\sqrt n).</math> In this case, <math>T \sim N(3200,400).</math> We know that <math>P(T>b) =.975.</math>So now we need to find the 97.5th percentile of this distribution using SOCR. According to the SOCR snapshot below, the 97.5th percentile of this distribution is 3984. Therefore b=3984. | |
<center>[[Image: SOCR_Activities_Normal_Christou_example3_e.jpg|600px]]</center> | <center>[[Image: SOCR_Activities_Normal_Christou_example3_e.jpg|600px]]</center> | ||
| - | + | <center></center>'''Answer:''' | |
| - | + | <center></center>a. <math>\overline{X} \sim N(\mu, \frac{\sigma}{\sqrt n }</math>. In this case, <math>\overline{X} \sim N(80000, 4518.48)</math>. | |
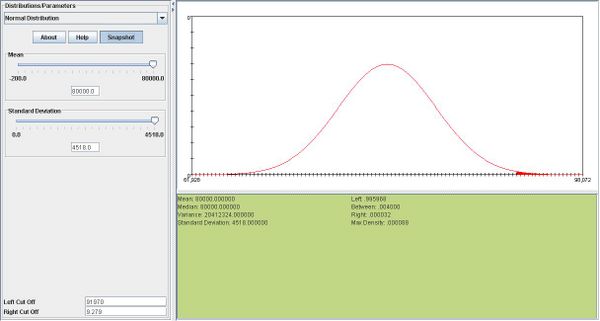
| - | + | <center></center>b. We can find the answer using SOCR. The answer is 0.004032. Please see snapshot below: | |
<center>[[Image: SOCR_Activities_Normal_Christou_example4_.jpg|600px]]</center> | <center>[[Image: SOCR_Activities_Normal_Christou_example4_.jpg|600px]]</center> | ||
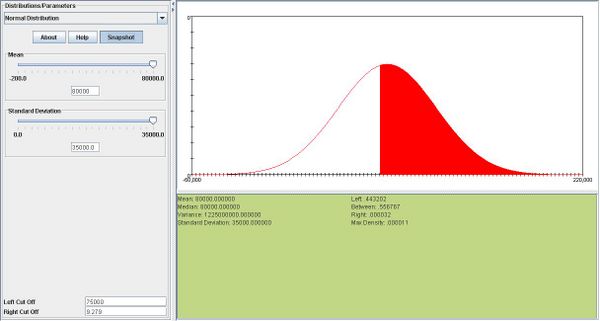
| - | + | <center></center>c. We can find the answer right away using SOCR. Please see snapshots below: | |
<center>This is the distribution for <math>X</math></center> | <center>This is the distribution for <math>X</math></center> | ||
<center>[[Image: SOCR_Activities_Normal_Christou_example4_c.jpg|600px]]</center> | <center>[[Image: SOCR_Activities_Normal_Christou_example4_c.jpg|600px]]</center> | ||
<center>This is the distribution for <math>\overline{X}</math></center> | <center>This is the distribution for <math>\overline{X}</math></center> | ||
<center>[[Image: SOCR_Activities_Normal_Christou_example3_c2.jpg|600px]]</center> | <center>[[Image: SOCR_Activities_Normal_Christou_example3_c2.jpg|600px]]</center> | ||
| - | + | <center></center>The probabilities are 55.6% for one hour vs. 86.6% for sample mean. Therefore the sample mean is more likely to be greater than 75000 hours. | |
| - | + | <center></center>'''Answer:''' | |
| - | + | <center></center>a. According to the SOCR snapshot below, the 75th percentile is 0.006115. | |
<center>[[Image: SOCR_Activities_Normal_Christou_example5_aa.jpg|600px]]</center> | <center>[[Image: SOCR_Activities_Normal_Christou_example5_aa.jpg|600px]]</center> | ||
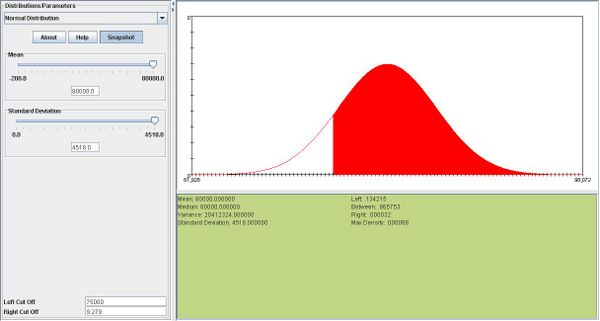
| - | + | <center></center>b.<math>P(X>.01)=.13.</math>We can see this in the snapshot below: | |
<center>[[Image: SOCR_Activities_Normal_Christou_example5_bb.jpg|600px]]</center> | <center>[[Image: SOCR_Activities_Normal_Christou_example5_bb.jpg|600px]]</center> | ||
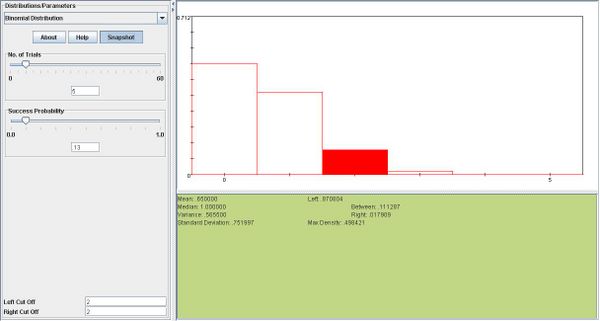
| - | + | <center></center><math>P(R=2)= (5 \choose 2) \times .13^2 \times .87^3= 0.11128. </math> | |
<center>[[Image: SOCR_Activities_Normal_Christou_example5_bc.jpg|600px]]</center> | <center>[[Image: SOCR_Activities_Normal_Christou_example5_bc.jpg|600px]]</center> | ||
| - | + | <center></center>c. <center></center> | |
i. <math>X \sim N(.00032,.00192)</math> | i. <math>X \sim N(.00032,.00192)</math> | ||
<center></center> | <center></center> | ||
Revision as of 21:51, 14 May 2007
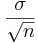 . Thus as the sample size increases, n increases, and as n increases, the standard deviation decreases.
. Thus as the sample size increases, n increases, and as n increases, the standard deviation decreases.
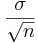
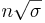 ; but the standard deviation of the sample mean is
; but the standard deviation of the sample mean is 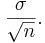 Unless n is one, the standard deviation of the total of a sample of n observations exceeds the standard deviation of the sample mean.
Unless n is one, the standard deviation of the total of a sample of n observations exceeds the standard deviation of the sample mean.
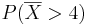 would be -2.828 while the z-score for P(X > 4) would be -2. P(Z > − 2.828) > P(Z > − 2). Therefore the statement is false.
would be -2.828 while the z-score for P(X > 4) would be -2. P(Z > − 2.828) > P(Z > − 2). Therefore the statement is false.
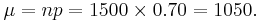 and
and 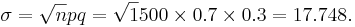
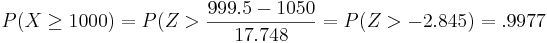
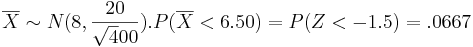
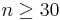 we can assume that the sample mean approaches the normal distribution. In this case n = 400. Therefore n satisfies the requirement of a large n.
we can assume that the sample mean approaches the normal distribution. In this case n = 400. Therefore n satisfies the requirement of a large n.
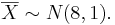 According to the snapshot below, the middle 80% of this distribution is (6.721,9.279). Therefore w = 8 − 6.721 = 1.29
According to the snapshot below, the middle 80% of this distribution is (6.721,9.279). Therefore w = 8 − 6.721 = 1.29
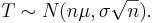 In this case,
In this case, 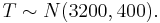 We know that P(T > b) = .975.So now we need to find the 97.5th percentile of this distribution using SOCR. According to the SOCR snapshot below, the 97.5th percentile of this distribution is 3984. Therefore b=3984.
We know that P(T > b) = .975.So now we need to find the 97.5th percentile of this distribution using SOCR. According to the SOCR snapshot below, the 97.5th percentile of this distribution is 3984. Therefore b=3984.
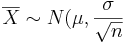 . In this case,
. In this case, 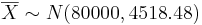 .
.
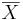
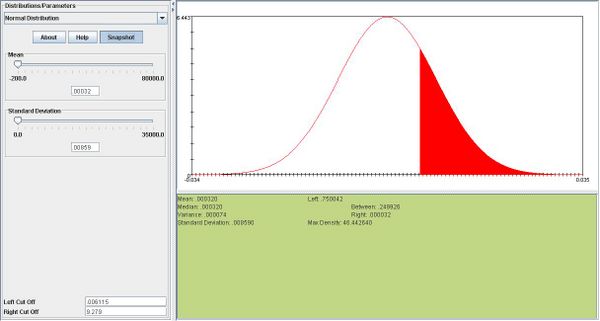
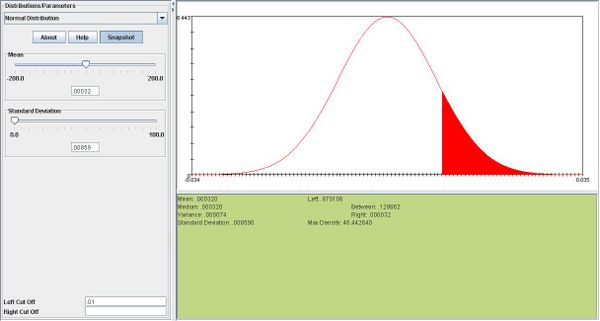
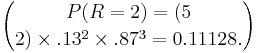
i. 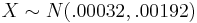
ii. 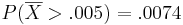
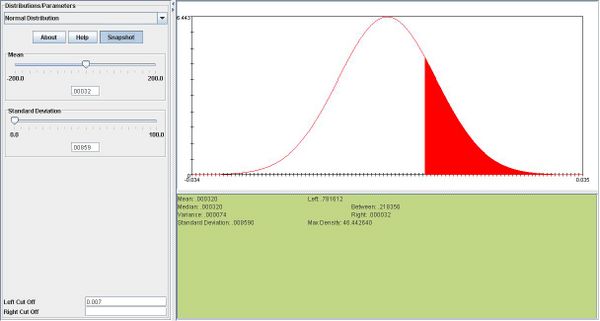
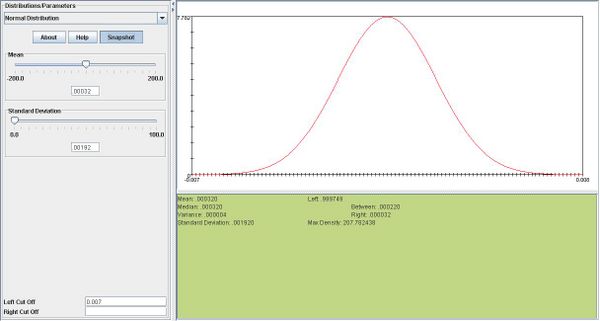
iii.One day's return is more likely to be greater than .007. The probabilities are 0.21 for X vs. .00022 for 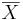 .
.